8. Сведение матричной игры к задаче линейного программирования
8.1. Смешанное расширение матричной игры
82. Сведение матричной игры к задаче ЛП
В матричных играх исследование начинается с нахождения седловой точки игры в чистых стратегиях. Если игра имеет седловую точку, то нахождением этой точки исследование игры заканчивается. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью.
Свойства решений матричных игр
Обозначим через G (Х,Y,А) игру двух лиц с нулевой суммой, в которой игрок 1 выбирает стратегию х Î Х, игрок 2 – y Î U, после чего игрок 1 получает выигрыш А = А (х, y) за счёт игрока 2.
Спектр смешанной стратегии игрока в конечной антагонистической игре есть множество всех его чистых стратегий, вероятность которых, согласно этой стратегии, положительна.
Свойство 1. Если чистая стратегия одного из игроков содержится в спектре некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации, образованной данной чистой стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антагонистической игры.
Свойство 2. Ни одна строго доминируемая чистая стратегия игрока не содержится в спектре его оптимальной стратегии.
Игра G¢ = (Х¢,Y¢,А¢) называется подыгрой игры G (Х,Y,А), если Х¢Ì Х, U¢Ì U, а матрица А¢ является подматрицей матрицы А. Матрица А¢ при этом строится следующим образом: в матрице А остаются строки и столбцы, соответствующие стратегиям Х¢ и U¢, а остальные вычеркиваются. Всё то что останется после этого в матрице А, будет матрицей А¢.
Свойство 3. Пусть G = (Х,Y,А) – конечная
антагонистическая игра, G¢ = (Х х¢,Y,А) – подыгра игры G, х¢ – чистая стратегия
игрока 1 в игре G, доминируемая некоторой стратегией 
,
спектр которой не содержит х¢. Тогда всякое решение (хо, yо, u) игры G¢ есть
решение игры G.
Свойство 4. Пусть G = (Х,Y,А) – конечная
антагонистическая игра, G¢ = (Х,Y y¢,А) – подыгра игры G, y¢ – чистая стратегия
игрока 2 в игре G, доминируемая некоторой стратегией 
,
спектр которой не содержит y¢. Тогда всякое решение подыгры G¢ есть решение G.
Свойство 5. Если для чистой стратегии х¢ игрока 1 выполнены условия свойства 3, а для чистой стратегии y¢ игрока 2 выполнены условия свойства 4, то всякое решение игры G¢ = (Х х¢,Y y¢,А) есть решение игры G = (Х,Y,А).
Свойство 6. Тройка (хо, yо, u) есть решение игры G = (Х,Y,А), только когда (хо, yо, кu +а) есть решение игры G(Х,Y,кА+а), где а – любое вещественное число, к > 0.
Свойство 7. Чтобы хо = (
)
была оптимальной смешанной стратегией матричной игры с матрицей А и ценой
игры u, необходимо и достаточно выполнение следующих неравенств
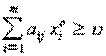(j = 
)
(*)
Аналогично для игрока 2: чтобы yо =
(
)
была оптимальной смешанной стратегией игрока 2, необходимо и достаточно
выполнение следующих неравенств:
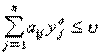(i
= 
)
(**)
Из последнего свойства вытекает: чтобы установить, суть ли предполагаемые (х, y) и u решение матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно с уравнениями
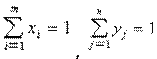(***) получим решение матричной игры.
Итак, решение матричной игры сводится к нахождению неотрицательных параметров решений линейных неравенств (*), (**) и линейных уравнений (***). Но это требует большого объёма вычислений, которое растёт
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
