Двойственность в математическом программировании и вообще в математике играет фундаментальную роль. Она выступает в качестве краеугольного камня соответствующих теорий, порождает арсенал конструктивных средств анализа математических моделей, построения эффективных алгоритмов решения задач и формальной оценки этой эффективности.
К каждой задаче ЛП можно построить своего рода симметричную: функционалы оптимальных решений у обеих задач совпадают, но если в прямой задаче они отражают наиболее эффективную комбинацию ресурсов, которая дает максимум целевой функции, то в другой – двойственной – наиболее эффективную комбинацию расчетных цен (оценок) ограниченных ресурсов – такие цены, при которых полученная продукция оправдывает затраты, а технологические способы, не включенные в план, по меньшей мере не более рентабельны, чем примененные.
Хотя принято считать прямой задачу, ориентированную на максимум целевой функции, и двойственной – ориентированную на минимум, на самом деле эти обозначения условны: обе задачи вполне равноправны, любую можно принять за прямую задачу и искать к ней двойственную задачу.
Двойственная задача состоит в минимизации затрат при заданных лимитах ресурсов и формулируется следующим образом:
Найти набор переменных v1, v2, ..., vn (называемых разрешающими множителями, объективно обусловленными (оптимальными) оценками, двойственными ценами и пр.), минимизирующий линейную функцию
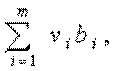
при том условии, что каждый включенный в план вид продукции рентабелен (полученная продукция оправдывает затраты), а невключенные в план – не более рентабельны, чем включенные.
Оценки характеризуют влияние свободных членов ограничений прямой задачи на оптимальную величину целевой функции; иначе говоря, показывают относительный вклад каждого ресурса в достижение оптимума; небольшое изменение количества ресурса изменяет оптимальное значение пропорционально величине оценки.
Двойственная задача в линейном программировании строится по формальным правилам на базе другой задачи линейного программирования, называемой основной задачей.
Например, если основная задача имеет вид
Ах ≤b , х≥0, f(с,х) → max, (1) то двойственная к ней задача тоже есть задача линейного программирования:
АТу≥ с, у≤0, f(b, у)→ min. (2)
Здесь х = (x1,х2,... ,хn); b = (b1, b2,…,bт); с = (с1, с2,..., сn); у = (y1,y2,... ,уm);
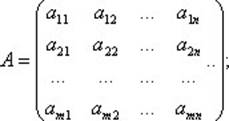
f(c,x)= 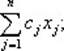 (3)
(3)
(b,y)= 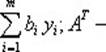 транспонированная
матрица A.
транспонированная
матрица A.
Основная и двойственная к ней задачи образуют пару взаимно двойственных задач: двойственная задача к двойственной оказывается основной задачей. Отношение между прямой и двойственной задачами выражается в виде следующих правил:
1) если прямая задача есть задача максимизации, то двойственная задача будет задачей минимизации и наоборот;
2) коэффициенты целевой функции прямой задачи с = (с1, с2,..., сn) становятся свободными членами ограничений двойственной задачи;
3) свободные члены ограничения прямой задачи b = (b1, b2,…,bт) становятся свободными членами целевой функции двойственной задачи;
4) матрица ограничений двойственной задачи получается транспонированием матрицы ограничения прямой задачи;
5) знаки неравенств в ограничениях изменяются на обратные;
6) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
Теорема формулируется так:
Либо обе задачи двойственной пары разрешимы, и тогда (с, х*) = (b, у*); либо обе задачи не имеют решения. Здесь х*,у* – оптимальные планы пары двойственных задач.
Эта и ряд других теорем, относящихся к двойственным задачам, играют важную роль при качественном анализе задач линейного программирования.
Содержательный анализ двойственной задачи, в том числе неизвестных у1, у2, ..., уm, полностью определяется содержательным смыслом прямой задачи. Так, например, если основная задача (1) есть задача производственного планирования, где А – технологическая матрица, bi – количество i-го ресурса, xj – объем выпуска j-го продукта, i = 1, 2, ... m, j = 1,
2, ... n, то целью решения двойственной задачи (2) оказывается нахождение так называемых двойственных оценок ресурсов yi, которые еще называются маргинальными (граничными) данными ресурсов.
Маргинальные цены связаны только с производством и потому отличаются от обычных рыночных цен на ресурсы. Если маргинальные цены не превосходят рыночных (уi*≤ qi, i=1,2,..., m), то производство, для которого они были рассчитаны, не сможет получить прибыль р от своей производственной деятельности: для любого плана выпуска x. р(х) = (с, х) - (b, q) ≤, (с, х*) - (b, q) ≤ (с, х*) - (b. у*) = 0.
И наоборот, если уi* > qi, i= 1, 2,..., m, то реализация оптимального производственного плана х* принесет положительную прибыль. р(х*) = (с, х*) - (b, q) = (А, у*) - (b, q) = (b, y*-q)> 0, размер которой ограничивается: а) средствами, выделяемым на закупку ресурсов;
b) объемом рынка ресурсов; с) технологическими условиями производства.
Из теоремы двойственности вытекает ряд положений, которые позволяют устанавливать некоторые соотношения между целевой функцией и ресурсами, необходимыми для достижения цели.
Итак, с математической точки зрения оптимальные оценки определяют влияние свободных членов b, условий-ограничений на оптимальную величину целевой функции. Иными словами, вычисление наряду с оптимальным планом х* = (х1*, х2*, ..., хn*) связанных с ним оптимальных оценок у* = {у1*, у2*, ... , ym*) позволяет ввести относительную важность отдельных ресурсов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.