Выбор регулятора при проектировании АСР, страница 2

Этот объект можно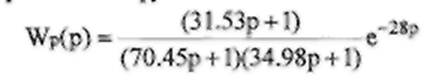представить как три последовательно соединенных звена -инерционное, инерционно-дифференцирующее и звено чистого запаздывания.

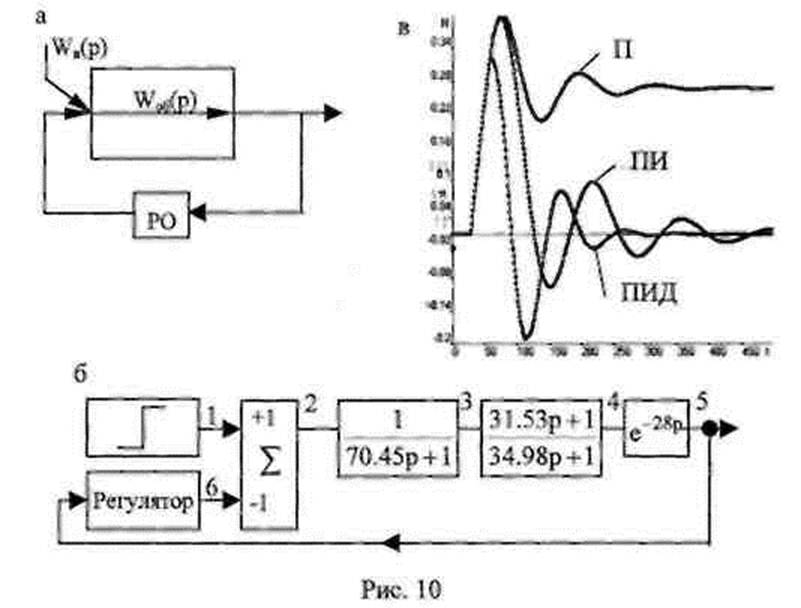
Возможны два случая возмущающего воздействия на объект управления. В первом случае возмущение наносится на вход объекта регулирования, где суммиру­ется с управляющим воздействием (рис. 10, а).

Составим таблицу звеньев (табл. 2) и таблицу данных (табл. 3) для одно­контурной АСР с возмущающим воздействием на вход объекта регулирования на базе декомпозированной системы регулирования. Для этого воспользуемся блок-схемой алгоритма моделирования переходного процесса (рис. 10, б).

№ звена	1	2	3	4	5	6
Кол звена	12	9	2	7	13	6
№ входа 1	0	1	2	3	4	5
№ входа 2	0	6	0	0	0	1     о

№ звена	1	2	3	4	5	6
Данные 1	1	1	1	1	28	3.5
Данные 2	0	-1	70.45	31.53	0	70
Данные 3	0	0	0	34.98	0	0

В приведенном примере в выделенных столбцах таблиц расположены дан­ные для ПИ-ре гул я тора. Для того, чтобы получить различные варианты переход­ных процессов в одноконтурной АСР в выделенных столбцах достаточно поменять

код звена (регулятора) (табл. 2) и занести соответствующие значения параметров настройки данного регулятора в табл. 3.

Из таблицы данных можно с приближенной точностью определить величи­ну шага интегрирования, умножив минимальную постоянную времени на 0,1, и вы­числить время интегрирования. Для этого максимальную постоянную времени нужно увеличить в пять - шесть раз.

Результат моделирования переходных процессов в одноконтурной АСР с возмущающим воздействием на вход объекта с различными регуляторами приведен на рис. 10, в.

Во втором случае воздействие на объект может наноситься в любую про­межуточную точку, при этом суммирование сигнала, поступающего по каналу воз­мущения, с сигналом, проходящим через объект регулирования, происходит как бы на выходе системы управления (рис. 11, а). Чтобы учесть характер данного возму­щения в одноконтурной АСР, необходимо внести соответствующие изменения в блок-схему алгоритма переходного процесса, как это показано на рис. 11,6.

№ звена	1	2	3	4	5	6	7	8
Код звена	12	2	13	9	6	2	2	13
№ входа 1	0	1	2	3	4	5	6	7
№ входа 2	0	1    о    |	1    о	8	0	0	0	0

№ звена	1	2	3	4	5	6	7	8
Данные 1	1	1	2,8	+ 1	2,75	1	1	28
Данные 2	0	70,45	0	-!	65	70,45	31,53	0
Данные 3	0	0	0	0	0	0	34,98	0

Здесь также в выделенных столбцах табл. 4 и 5 приведены данные для ПИ-регулятора. Чтобы получить результаты моделирования переходных процессов в одноконтурной АСР с другими типами регуляторов, нужно поменять код регулято­ра в табл. 4 и записать его параметры настройки в табл. 5.

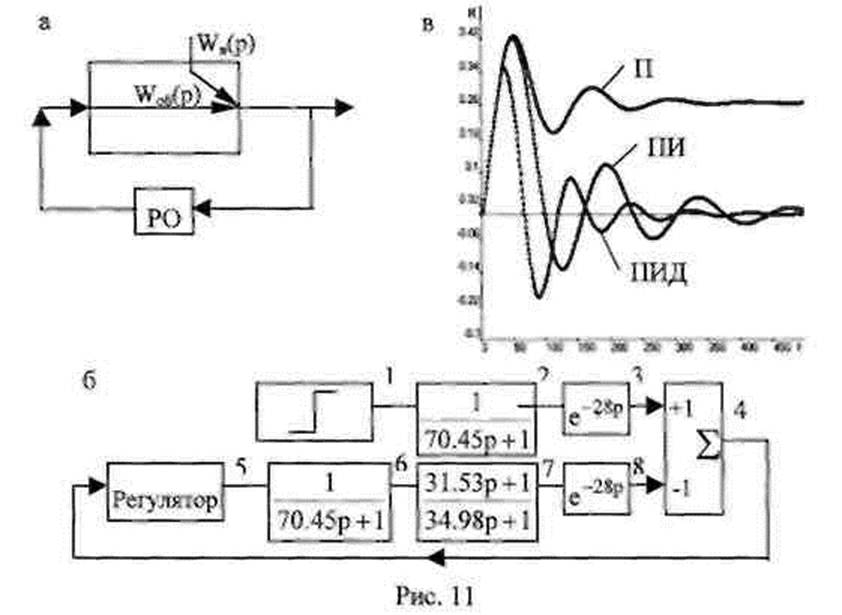
Результат моделирования переходных процессов в одноконтурной АСР с нанесенным возмущающим воздействием в промежуточную точку при использова­нии различных регуляторов приведен на рис. 11, в.

8. Оценка эффективности работы различных регуляторов в одноконтурной АСР по величине динамического коэффициента регулирования

Степень воздействия регулятора, понижающего динамическое отклонение, характеризуется динамическим коэффициентом регулирования Кд, который пред­ставляет собой отношение максимального отклонения регулируемой величины от заданного значения hi в переходном процессе регулирования, вызванном каким-либо однократным скачкообразным возмущением, к отклонению от заданного зна­чения при том же возмущении, но без регулирующего воздействия:

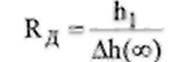
Величина потенциального отклонения от заданного значения ДЬ(со) харак­теризует свойства объекта регулирования и величину возмущения. Очевидно, что Дп(со) = кобУв, где коб- коэффициент передачи объекта, у_в - величина возмущения. Анализируя графики зависимости динамического коэффициента регулирования Яд от величины отношения т/Т (динамические свойства объекта) для АСР с регулято­рами непрерывного действия, можно сделать следующие выводы. Динамический ...коэффициент регулирования, а значит, и .максимальное динамическое отклонение регулируемой величины от заданного значения всегда больше, если используется И-регулятор. Использование П- и ПИ-регуляторов для аналогичных процессов позво­ляет значительно уменьшить величину динамического коэффициента регулирова­ния. И, наконец, наилучшее - минимальное - значение Яд можно получить, исполь­зуя ПИД-регулятор. Для переходных процессов с 20%-м перерегулированием при различных значениях отношения т/Т сведены в табл. 6.

Таблица 6

хГТ	0,1	0,2	0,3	0,4	0,5	0,8	1
Клгп/ Кд(щ	0,33	0,46	0,57	0,65	0,72	0,9	0,95
»М1«ШУ Кл(И1	0,29	0,42	0,53	0,63	0,7	0,88	0,94
Кдшилу Rnmm	0,64	0,72	0,78	0,8	0,8	0,8	0,81

При анализе приведенных данных видно, что для ПИД-регуляторов при ма­лых значениях т/Т (от 0,1 до 0,2) можно уменьшить максимальное отклонение в 1,5 раза, а при ббльших значениях т/Т - только на 25 - 30%.

Общей тенденцией для всех типов регуляторов является то, что с увеличе­нием отношения т/Т динамический коэффициент регулирования стремится к еди­нице, т. е. эффективность работы регуляторов резко снижается. Приведенные зна­чения функции Яд = У(т/Т) позволяют рассчитывать один из основных критериев качества регулирования - максимальное динамическое отклонение регулируемой величины.