Министерство образования Республики Беларусь.
Гомельский государственный технический университет имени П. О. Сухого
Кафедра
“ Информационные технологии ”
Курсовая работа по курсу
Принял преподаватель
СОДЕРЖАНИЕ
Введение……………………………………………………………………..….3
1. ПОСТАНОВКА ЗАДАЧИ……………………………………………………4
2.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ К РАБОТЕ………………………………5
3. СИСТЕМНОЕ И ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЭВМ………………6
4.РАЗРАБОТКА СТРУКТУРЫ ПРОГРАММЫ…………………………….7
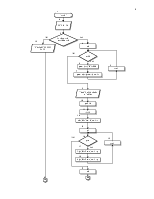
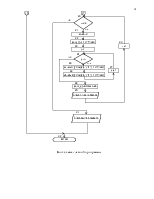
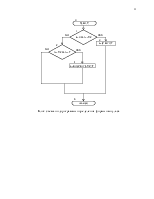
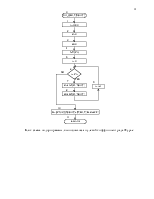
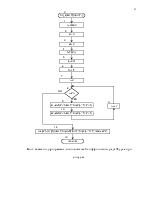
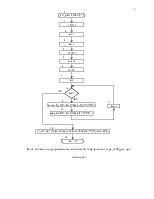
5.РАЗРАБОТКА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ ……………………………………………………………………………….………8
6.АНАЛИЗ ПОЛУЧЕНННЫХ РЕЗУЛЬТАТОВ……………………………..15
7. ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЮ…………………………………………15
ЗАКЛЮЧЕНИЕ………………………………………………………………..16
ПРИЛОЖЕНИЕ 1 (ЛИСТИНГ ПРОГРАММЫ)
Введение
Внедрение компьютерной техники в работу, производственные процессы, научные исследования и быт человека привело к увеличению разработки разнообразного программного обеспечения, направленного на облегчение расчетов и работы человека.
Данная курсовая работа является примером такого программного обеспечения, облегчающего, расчет ряда Фурье для аппроксимации заданного несинусоидального импульса треугольного вида.
1. ПОСТАНОВКА ЗАДАЧИ.
Задача: Разложить несинусоидальный импульс треугольного вида в ряд Фурье с заданным количеством гармоник периодом и максимальной ЭДС.
В представленной курсовой работе предполагается, что разрабатываемая программа должна использоваться как средство изучения и анализа определенного несинусоидального импульса. Одним из основных условий должно быть удобство работы пользователя и доходчивый, понятный интерфейс. Программа должна осуществлять:
• Ввод исходных данных;
• Расчет результатов;
• Вывод результатов;
Для правильного функционирования программы необходимы данные определяющие параметры исследуемого импульса.
Важным аспектом является то, что в процессе обработки данные и результаты необходимо использовать максимально точно для точности построения графика ряда.
2.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ К РАБОТЕ.
Спектром временной зависимости x(t) называется совокупность её гармонических состовляющих, образующих ряд Фурье.
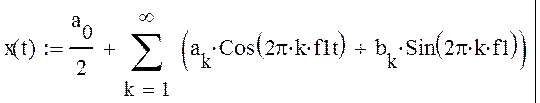
Где t-время ,
f1-частота (f1=1/T),
T-период повторения функции,
К- номер гармоники, ак, bk- коэфициенты Ряда Фурье которые определяются по формулам:
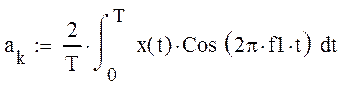
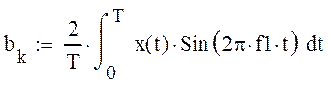
Для вычисления определённых интегралов используется метод Симпсона.
Описание метода Симпсона
Для вычисле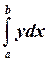ния 
промежуток от a(x0) до
b(xn) разбивается на n равных частей, и для точек деления x0
, x1 , x2 , x3 , . . . , xn-1 , xn
вычисляются значения интегрируемой функции y. Затем необходимо воспользоваться
формулой приближённого интегрирования:
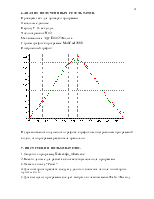
Формула Cимпсона (парабол) (рис.1) :
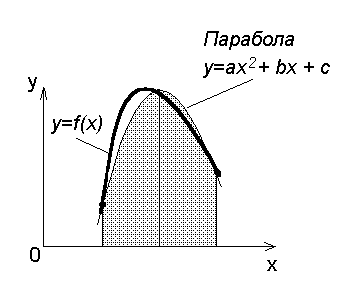
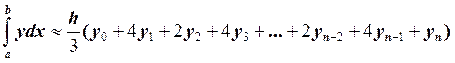
3. СИСТЕМНОЕ И ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЭВМ
Программный продукт представлен одним независимым исполняемым файлом Kursovaja_rabota.exe, размер которого составляет 688128 байт.
Для работы с данной программой необходимо следующее системное и программное обеспечение ЭВМ:
1. Минимальный объем жесткого диска 10 МБ.
2. Процессор не ниже Intel80486.
3. Операционная система MS Windows 98 и выше.
4. Любой графический монитор.
5. Клавиатура.
6. Дисковод.
4.РАЗРАБОТКА СТРУКТУРЫ ПРОГРАММЫ.
Вданной курсовой работе были использованы следующие компоненты среды программирования C++Builder:
TForm: компонент для создания основного окна программы.
TMainMenu: компонент для создания главного меню.
Chart: компонент для создания графиков и диаграмм.
Tbutton: этот компонент создаёт прямоугольную кнопку с надписью. Щелчок на кнопке генерирует событие OnClick, на которое программа реагирует определённым образом.
TEdit: редактируемая строка для ввода и вывода данных.
TLabel: метка, используется для пояснения предписанного компонента.
TStringGrid: компонент для создания текстовой таблицы.
TStaticText: используетсядля создания текста на форме, который можно редактировать.
Программа разбита на подпрограммы, в данном случае они будут нисходящими блоками схемы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.