Разработка программного комплекса аналитической аппроксимации вебер-амперной характеристики нелинейной индуктивности методом выбранных точек в среде BorlandC++Builder 5

нажатии на стрелку вверх или вниз соответственно увеличивается или уменьшается значение переменой cur.

· при нажатии на кнопку Enter происходит выбор пункта меню, на котором находится курсор, и в связи с этим на какой строке находится курсор записывается значение ch=n-1где n-номер строки. По номеру ch выполняются следующие действия:

0: Ввод данных

1: Изменение данных

2: Расчет данных

3: Построение графика

4: Сохранение данных в файл

5: Выход

Ввод данных: здесь осуществляется ввод исходных данных в переменные (n и массив a[i])

Изменение данных здесь происходит корректировка введенных данных, т. е. защита от неправильного ввода чисел. Это осуществляется следующим образом: программа выводит все значения точек, которые были введены под определенным номером, потом она просит ввести номер точки которую нужно исправить, пользователь вводит новую переменную и она записывается на место старой переменной в тот же массив a[i].

Расчет данных  при выборе этого пункта меню, выполняется расчет данных по методу Крамера, описанного в пункте 1.1. После расчета коэффициентов, их значения выводятся на экран, вместе со значениями аппроксимирующей функции.

Для отображения полученных значений исходной и аппроксимирующей функций в виде графика служит следующий пункт меню Построение графика. Здесь строятся графики с автоматическим масштабированием. Программа разлинеивает координатную сетку, потом автоматически считает где должны стоять точки и строит их. Вычисление производится с помощью переменных x, y,x1,y1. x1 и y1 – это расстояние каждой клеточки на координатных осях.

Сохранение данных в файл – здесь происходит сохранение вычисленных данных a₁,a₂,a₃ … a_n –аппроксимирующей функции. Программа просит ввести название файла. Пользователь вводит название файла, и он сохраняется в этом же каталоге с программой, под тем именем которое было введено.

Выход – выход из программы.

Схема иерархии программного комплекса приведена на рис. 5.1

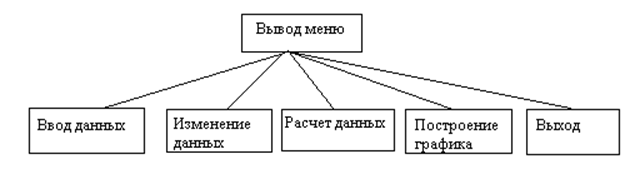
Рисунок 5.1 Схема иерархии программы

Графические схемы алгоритмов пунктов меню приведены на рисунках 5.2 -5.5, и таблицы соответствия переменных в таблице  5.1

 

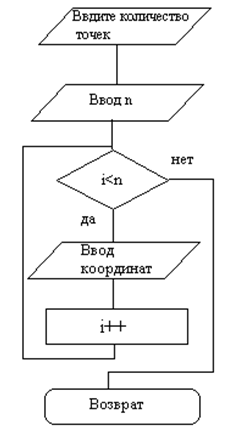Рисунок 5. 2. Графическая схема алгоритма «Ввод данных»

 

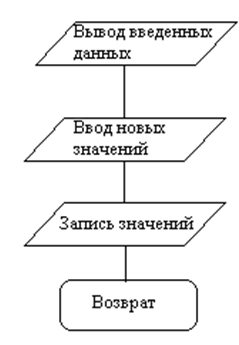Рисунок 5.3 Графическая схема алгоритма «Изменение данных»

 

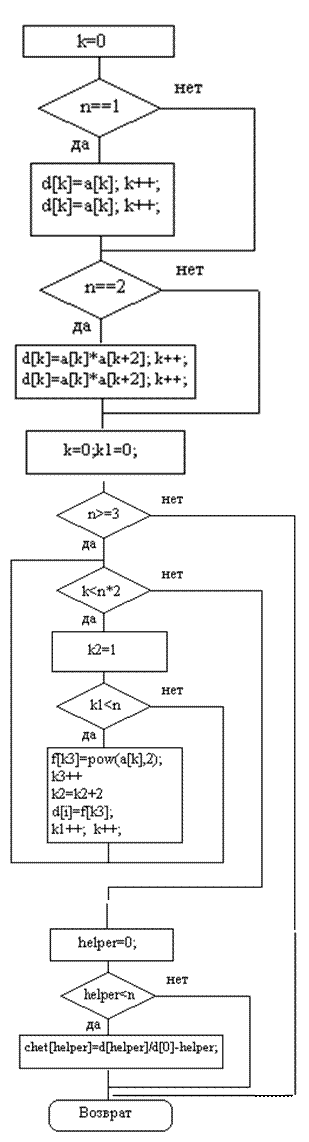Рисунок 5.4 Графическая схема алгоритма «Расчет данных»

 

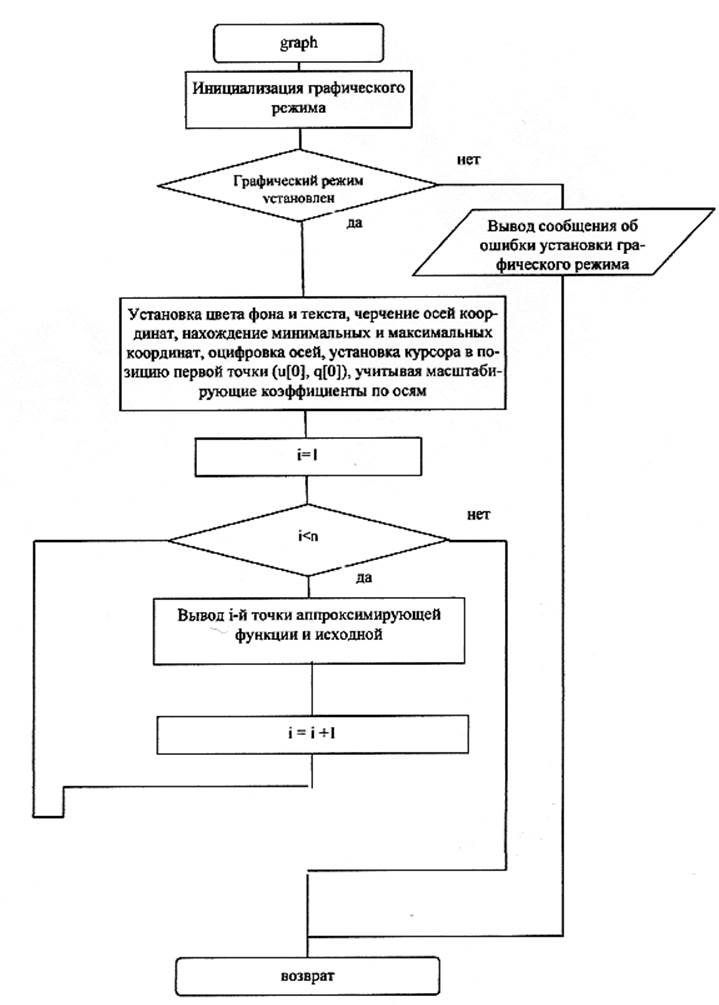Рисунок 5.5 Графическая схема алгоритма «Построение графика»

 

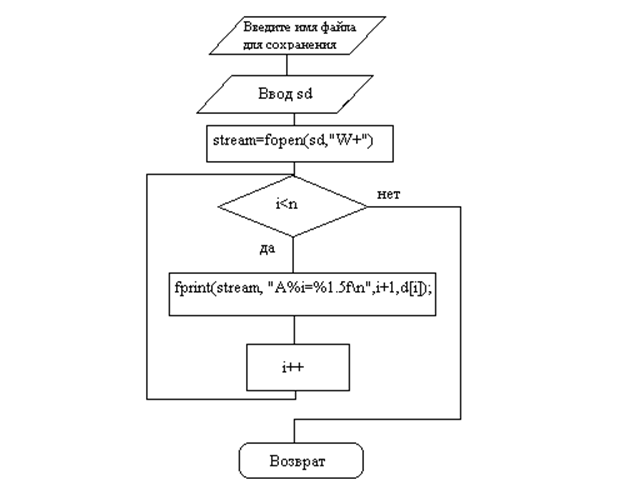Рисунок 5.6 Графическая схема алгоритма «Сохранение в файл»

Таблица 5.1 Таблица соответствия переменных программы.

Имя переменной в программе	Тип переменной	Комментарий
n	int	Количество точек
I	int	Переменная , служащая, счетчиком
j	int	Переменная , служащая, счетчиком
a	float	Массив в котором содержатся и изменяются введенные данные
d,f,g,z,t,chet	float	Массивы, для расчета уравнений по методу Крамера
x,y,x1,y1	float	Переменные, содержащие данные о расстояниях от точки до точки на графике
sd	char	Строка, использующаяся для заголовка имени файла сохранения
b,c,kserox,ks,ks1	int	Переменные счетчики
temp3…temp8	float	Переменные счетчики

Заключение

Из проделанной мною работы можно сделать вывод, что ЭВМ в инженерных расчётах просто необходимо, т.к. это является удобным и качественным методом расчёта. Производить инженерный расчёт в ручную очень сложно и в нём можно легко запутаться, в чём я убедился, проделав курсовую работу, а написав программу на ЭВМ нет опасений по поводу неправильных расчетов.

Задание, поставленное на курсовую работу выполнено. Была написана программа, позволяющая вводить, изменять, рассчитывать, строить график и сохранять данные в файл, значений аппроксимации вебер-амперной характеристики нелинейной индуктивности методом выбранных точек.

В программе возможно аппроксимировать функцию n точками. У нее удобный и красивый интерфейс.

Литература

1.  Апатенок Р. Ф. Элементы линейной алгебры. – М.: Высшая школа, 1985, 240 с.

2.  Самарский А. А., Гулин А. В., Численные методы. – М.: Наука, 1989, 432с.

3.  А. И. Касаткин, А. Н. Вальвачев., Профессиональное программирование на языке С: Справочное пособие.–Мн.: Высшая школа, 1992. – 240с.

ПРИЛОЖЕНИЕ А

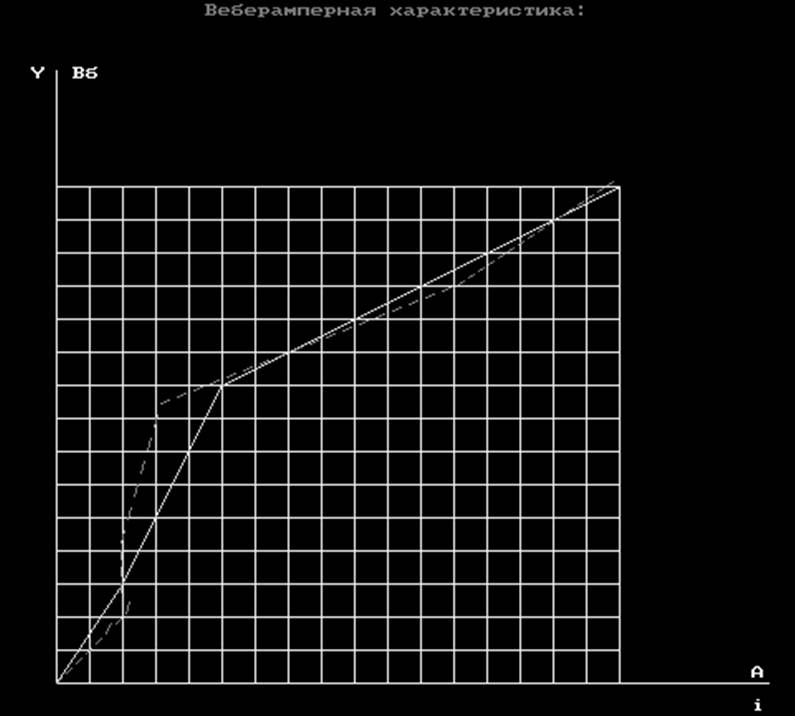
Результаты

Расчет значений по введенным данным:

Если ограничиваться тремя членами, то функция апроксимации имеет вид:

i=a1*Y+a2*Y(3)+a3*Y(5)

При n-ом количестве точек функция апроксимации примет вид:

i=a1*Y+a2*Y(3)+a3*Y(5)+...+an*Y(n)

Решая полученную систему методом Крамера находим:

A1=0.55000

A2=-8487.65430

A3=325788896.00000

Нажмите Enter для продолжения...

 

Приложение Б

Листинг программы

//Курсовая работа ст. гр. ПЭ-22 Блудчего А.В.

#include<stdio.h>

#include<math.h>

#include<conio.h>

#include <stdlib.h>

#include<graphics.h>

#include <iostream.h>

char main_menu[]={"   Ввод данных    "

" Изменение данных "

"   Расчет данных  "

"Построение графика"

"Сохранение в файл "

"      Выход       "};

void move_cur_up(char *text,int strlen,int pos)

{

gotoxy(2,2+pos);

textcolor(WHITE);

textbackground(BLUE);

for(int i=0;i<strlen;i++)

cprintf("%c",text[i+pos*strlen]);

gotoxy(2,2+pos-1);

textcolor(BLACK);

textbackground(WHITE);

for(i=0;i<strlen;i++)

cprintf("%c",text[i+(pos-1)*strlen]);

}

void move_cur_dn(char *text,int strlen,int pos)

{

gotoxy(2,2+pos);

textcolor(WHITE);

textbackground(BLUE);

for(int i=0;i<strlen;i++)

cprintf("%c",text[i+pos*strlen]);

gotoxy(2,2+pos+1);

textcolor(BLACK);

textbackground(WHITE);

for(i=0;i<strlen;i++)

cprintf("%c",text[i+(pos+1)*strlen]);

}

void inverse(char *text,int strlen,int cur=0)

{

gotoxy(2,2+cur);

textcolor(BLACK);

textbackground(WHITE);

for(int i=0;i<strlen;i++)

cprintf("%c",text[i+cur*strlen]);

}

void reverse(char *text,int strlen,int cur=0)

{

gotoxy(2,2+cur);

textcolor(WHITE);

textbackground(BLUE);

for(int i=0;i<strlen;i++)

cprintf("%c",text[i+cur*strlen]);

}

void show(char *text,int numl,int strlen)

{

gotoxy(2,2);

for(int i=0;i<numl;i++)

{

for(int j=0;j<strlen;j++)

cprintf("%c",text[j+i*strlen]);

gotoxy(2,2+i+1);

}

}

void Show_Window(int lx,int ly,int rx,int ry,char *header="Меню")

{

textattr(BLACK*16|WHITE);

clrscr();

textattr(BLUE*16|WHITE);

window(lx,ly,rx,ry);

clrscr();

gotoxy(1,1);

cprintf("%c",201);

for(int i=2;i<=(rx-lx);i++)

cprintf("%c",205);

cprintf("%c",187);

for(i=2;i<=(ry-ly);i++)

{

gotoxy(1,i);

cprintf("%c",186);

gotoxy(rx-lx+1,i);

cprintf("%c",186);

}

gotoxy(1,ry-ly+1);

cprintf("%c",200);

for(i=2;i<=(rx-lx);i++)

cprintf("%c",205);

cout<<(char)188;

gotoxy(7,1);

if(header)

{

textattr(BLUE*16|WHITE);

cprintf("[");

textattr(BLUE*16|LIGHTRED);

cprintf("%s",header);

textattr(BLUE*16|WHITE);

cprintf("]");

}

}

main()

{ int n,i,j,s,k,k1,k2,q,w,rt,kol,lp,k3=0,x3=7,y3=2,x4=3,x5=5,x6=6;

int b[100],c[100],kserox=0,ks=140,ks1=320,ks2=418;;

float d[100],f[100],g[100],perem1,perem2,z[100],t[100],chet[100];

float x,y,x1,y1,temp1=0,temp2=0;

float temp3=0,temp4=0,temp5=0,temp6=0,temp7=80,temp8=430;

float v=0,m=0,l=0,p=0,o[100],u[100];

char sd[10];

float a[100];

FILE *stream;

char ch;

Again:

int cur=0;

textattr(BLACK*16|WHITE);

clrscr();

Show_Window(27,7,46,14);  //Размеры рамки меню

show(main_menu,6,18);

inverse(main_menu,18);

while((ch=getch())!=27)

{

switch(ch)

{

case 72:if(cur==0)

{

reverse(main_menu,18,cur);

cur=5;

inverse(main_menu,18,cur);

break;

}

move_cur_up(main_menu,18,cur);

cur--;

if (cur>=5) cur=4;

break;

case 80:

if(cur==2)

{

reverse(main_menu,18,cur);

cur=3;

inverse(main_menu,18,cur);

break;

}

move_cur_dn(main_menu,18,cur);

cur++;

if (cur>=6) {

//cur=3;

cur=0;

Show_Window(27,7,46,14);

show(main_menu,6,18);

inverse(main_menu,18);

}

break;

case 13:switch(cur)

{

case 0:

{window(1,1,80,25);

textbackground(BLACK);

textcolor(WHITE);

clrscr();

textcolor(14);

cprintf("Введите количество точек: ");

scanf("%d",&n);

textcolor(12);

cprintf("Введите значения функции Y(A):");

printf("\n");

j=0;

s=1;

textcolor(11);

for(i=0;i<n;i++)

{cprintf("%d-ая точка(по оси y): ",s);

scanf("%f",&a[j]);

j++;

cprintf("%d-ая точка(по оси x): ",s);

scanf("%f",&a[j]);

j++;

s++;

}

goto Again;

}

case 1: {

window(1,1,80,25);

textbackground(BLACK);

textcolor(WHITE);

clrscr();

textcolor(14);

gotoxy(26,1);

printf("Изменение данных:\n");

printf("Введенные данные:\n");

j=0;

s=1;

textcolor(11);

for(i=0;i<n;i++)

{printf("%d. %d-ая точка(по оси y): =%f\n",j+1,s,a[j]);

j++;

printf("%d. %d-ая точка(по оси x): =%f\n",j+1,s,a[j]);

j++;

s++;

}

printf("%d.Выход в предыдущее меню\n",j+1);

printf("Выберите пункт меню: ");

scanf("%d",&lp);

for(i=1;i<=n;i++)

{ if (lp==i)

{printf("Введите новое значение точки: ");

scanf("%f",&a[i-1]);}

}

for(i=n+1;i<=n*2;i++)

{ if (lp==i)

{printf("Введите новое значение точки: ");

scanf("%f",&a[i-1]);}

}

if (lp==n*2+1) goto Again;

goto Again;

}

case 2:

{window(1,1,80,25);

textbackground(BLACK);

textcolor(WHITE);

clrscr();

//Расчет величин по введенным данным по методу Крамера

k=0;

if (n==1)

{d[k]=a[k]; k++;

d[k]=a[k]; k++;

}

k=0;

if (n==2)

{ d[k]=a[k]*a[k+2]; k++;

d[k]=a[k]*a[k+2]; k++;

}

k=0;

k1=0;

k2=1;

k3=0;

if (n==3)   //Рассчет матрицы

{ for(k=0;k<n*2;k=k+2)

{ k2=1;

for(k1=0;k1<n;k1++)

{f[k3]=pow(a[k],k2);

k3++;

k2=k2+2;

}

}

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((f[k]*f[k+4]*f[k+8])+(f[k+3]*f[k+7]*f[k+2])+(f[k+1]*f[k+5]*f[k+6]));

perem2=(f[k+6]*f[k+4]*f[k+2])+(f[k+3]*f[k+1]*f[k+8])+(f[k+7]*f[k+5]*f[k]);

g[0]=perem1-perem2;

k3=0;

for(k=0;k<n*2;k=k+2)

{ k2=1;

for(k1=0;k1<n;k1++)

{f[k3]=pow(a[k],k2);

k3++;

k2=k2+2;

}

}

f[0]=a[1]; f[3]=a[3]; f[6]=a[5];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((f[k]*f[k+4]*f[k+8])+(f[k+3]*f[k+7]*f[k+2])+(f[k+1]*f[k+5]*f[k+6]));

perem2=(f[k+6]*f[k+4]*f[k+2])+(f[k+3]*f[k+1]*f[k+8])+(f[k+7]*f[k+5]*f[k]);

g[1]=perem1-perem2;

k3=0;

for(k=0;k<n*2;k=k+2)

{ k2=1;

for(k1=0;k1<n;k1++)

{f[k3]=pow(a[k],k2);

k3++;

k2=k2+2;

}

}

f[1]=a[1]; f[4]=a[3]; f[7]=a[5];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((f[k]*f[k+4]*f[k+8])+(f[k+3]*f[k+7]*f[k+2])+(f[k+1]*f[k+5]*f[k+6]));

perem2=(f[k+6]*f[k+4]*f[k+2])+(f[k+3]*f[k+1]*f[k+8])+(f[k+7]*f[k+5]*f[k]);

g[2]=perem1-perem2;

k3=0;

for(k=0;k<n*2;k=k+2)

{ k2=1;

for(k1=0;k1<n;k1++)

{f[k3]=pow(a[k],k2);

k3++;

k2=k2+2;

}

}

f[2]=a[1]; f[5]=a[3]; f[8]=a[5];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((f[k]*f[k+4]*f[k+8])+(f[k+3]*f[k+7]*f[k+2])+(f[k+1]*f[k+5]*f[k+6]));

perem2=(f[k+6]*f[k+4]*f[k+2])+(f[k+3]*f[k+1]*f[k+8])+(f[k+7]*f[k+5]*f[k]);

g[3]=perem1-perem2;

//Вычисление a1, a2,a3

d[0]=g[1]/g[0];

d[1]=g[2]/g[0];

d[2]=g[3]/g[0];

}

//Если количество точек превышает 3

if (n==4)

{  int koll=0;

while(koll<=n-1)

{

k=0;

k1=0;

k2=1;

k3=0;

k3=0;

for(k=0;k<n*2;k=k+2)

{ k2=1;

for(k1=0;k1<n;k1++)

{f[k3]=pow(a[k],k2);

k3++;

k2=k2+2;

}

}

if (koll==1) {f[0]=a[1];}

if (koll==2) {f[1]=a[1];}

if (koll==3) {f[2]=a[1];}

if (koll==4) {f[3]=a[1];}

k=0; k1=0;

v=f[0];

z[0]=f[5];z[1]=f[6];z[2]=f[7];z[3]=f[9];z[4]=f[10];z[5]=f[11];z[6]=f[13];

z[7]=f[14];z[8]=f[15];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((z[k]*z[k+4]*z[k+8])+(z[k+3]*z[k+7]*z[k+2])+(z[k+1]*z[k+5]*z[k+6]));

perem2=(z[k+6]*z[k+4]*z[k+2])+(z[k+3]*z[k+1]*z[k+8])+(z[k+7]*z[k+5]*z[k]);

g[0]=(perem1-perem2)*v;

m=f[1];

t[0]=f[4];t[1]=f[6];t[2]=f[7];t[3]=f[8];t[4]=f[10];t[5]=f[11];t[6]=f[12];

t[7]=f[14];t[8]=f[15];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((t[k]*t[k+4]*t[k+8])+(t[k+3]*t[k+7]*t[k+2])+(t[k+1]*t[k+5]*t[k+6]));

perem2=(t[k+6]*t[k+4]*t[k+2])+(t[k+3]*t[k+1]*t[k+8])+(t[k+7]*t[k+5]*t[k]);

g[1]=((perem1-perem2)*m)*(-1);

l=f[2];

o[0]=f[4];o[1]=f[5];o[2]=f[7];o[3]=f[8];o[4]=f[9];o[5]=f[11];o[6]=f[12];

o[7]=f[13];o[8]=f[15];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((o[k]*o[k+4]*o[k+8])+(o[k+3]*o[k+7]*o[k+2])+(o[k+1]*o[k+5]*o[k+6]));

perem2=(o[k+6]*o[k+4]*o[k+2])+(o[k+3]*o[k+1]*o[k+8])+(o[k+7]*o[k+5]*o[k]);

g[2]=(perem1-perem2)*l;

p=f[3];

u[0]=f[4];u[1]=f[5];u[2]=f[6];u[3]=f[8];u[4]=f[9];u[5]=f[10];u[6]=f[12];

u[7]=f[13];u[8]=f[14];

perem1=0; perem2=0; k=0; k1=0; k2=0;

perem1=((u[k]*u[k+4]*u[k+8])+(u[k+3]*u[k+7]*u[k+2])+(u[k+1]*u[k+5]*u[k+6]));

perem2=(u[k+6]*u[k+4]*u[k+2])+(u[k+3]*u[k+1]*u[k+8])+(u[k+7]*u[k+5]*u[k]);

g[3]=((perem1-perem2)*p)*(-1);

d[koll]=g[0]+g[1]+g[2]+g[3];

koll++;

}

chet[0]=d[1]/d[0];

chet[1]=d[2]/d[0];

chet[2]=d[3]/d[0];

chet[3]=d[4]/d[0];

} //Конец расчета если матрица превышает 3*3

if(n>=5)

{

int helper;

for(helper=0;helper<n;helper++)

chet[helper]=d[helper]/d[0]-helper;

}

//Вывод поясняющих сообщений

gotoxy(26,1);

printf("Расчет значений по введенным данным:\n");

printf("Если ограничиваться тремя членами, то функция апроксимации имеет вид:\n");

textcolor(12);

printf("i=a1*Y+a2*Y(3)+a3*Y(5)\n");

textcolor(WHITE);

printf("При n-ом количестве точек функция апроксимации примет вид:\n");

textcolor(12);

printf("i=a1*Y+a2*Y(3)+a3*Y(5)+...+an*Y(n)\n");

printf("Решая полученную систему методом Крамера находим:\n");

textcolor(14);

if (n<=3)

{

for(i=0;i<n;i++)

{printf("A%i=%1.5f\n",i+1,d[i]);

}

}

if (n>3)

{

for(i=0;i<n;i++)

{printf("A%i=%1.5f\n",i,chet[i]);

}

}

textcolor(WHITE);

printf("Нажмите Enter для продолжения...");

//   scanf("%d",lp);

getch();

goto Again;}

case 3:

{window(1,1,80,25);

textbackground(BLACK);

textcolor(WHITE);

clrscr();

temp3=0;temp4=0;temp5=0;temp6=0;temp7=80;temp8=430;

//Вычисление расстояния между квадратами на осях координат

y=0;

q=0;

for(i=0;i<n;i++)

{ y=y+a[q];

q=q+2;

}

x=0;

q=1;

for(i=0;i<n;i++)

{ x=x+a[q];

q=q+2;

}

/* Автоопределение графики */

int gdriver = DETECT, gmode, errorcode;

/* Инициализация графики и переменных */

initgraph(&gdriver, &gmode, "");

/* Чтение результатов инициализации */

errorcode = graphresult();

/* Проверка на ошибку */

if (errorcode != grOk)

{

printf("Graphics error: %s\n", grapherrormsg(errorcode));

printf("Press any key to halt:");

getch();

exit(1);

}

setcolor(YELLOW);

/* Рисуем диагональную линию */

line(80,60,80,430);

line(80,430,510,430);

//Построение сетки для координатных осей

k=0;

k1=100;

for(k=1;k<18;k++) //21

{ line(k1,130,k1,430);

k1=k1+20;

}

k2=430;

k=0;

for(k=1;k<17;k++)

{ line(80,k2,420,k2);

k2=k2-20;

}

//Подписывание осей

moveto(65,58);

outtext("Y");

moveto(90,58);

outtext("Вб");

moveto(500,420);

outtext("A");

moveto(500,440);

outtext("i");

//Вывод сообщения на экран

moveto(170,20);

setcolor(12);

outtext("Веберамперная характеристика:");

moveto(20,30);

//Построение графика по введенным данным

//расчет коээфициентов под координатную сетку

setcolor(11);

x1=0; y1=0;

x1=x/17;

y1=y/15;

temp5=80;

temp6=430;

q=0;

int q1=1;

for(i=0;i<=n-1;i++)

{ temp1=0;

temp2=0;

while(temp1<a[q1])

{ temp2=temp2+20;

if ((temp5+temp2)>420) temp2=temp2-20;

temp1=temp1+x1;

}

temp3=0;

temp4=0;

while(temp3<a[q])

{ temp4=temp4+20;

if ((temp6-temp4)<130) temp4=temp4-20;

temp3=temp3+y1;

}

temp5=temp5+temp2;

temp6=temp6-temp4;

if(i>0)

{if (a[q]==a[q-2])

{ temp6=temp6+temp4;}

}

if(i>0)

{if (a[q1]==a[q1-2])

{ temp5=temp5-temp2;}

}

line(temp7,temp8,temp5,temp6);

temp7=temp5;

temp8=temp6;

if (i==0) {kserox=temp7-10;}

q=q+2;

q1=q1+2;

}

setcolor(LIGHTMAGENTA);

int j=83;

int j1=427;

moveto(80,430);

while(j<kserox)

{lineto(j,j1);

moveto(j+x4,j1-x4);

j=j+x6;

j1=j1-x6;

}

while(j<=kserox+3)

{ lineto(j,j1-x4);

moveto(j+x4,j1-x4);

j=j+x6;

j1=j1-x6;

}

int kser=375;

kserox=j;

lineto(j,j1);j=j+x4; j1=j1-x4; moveto(j,j1); j1=j1-x3;  lineto