Данная курсовая работа предназначена для расчета параметров аппроксимирующей функции методом выбранных точек с помощью программы на языке программирования Си.
1.Постановка задачи
Требуется разработать программу на языке Си, позволяющую вводить исходные данные, производить по ним расчет, а также осуществлять вывод полученных результатов на экран и на принтер. Программа должна содержать меню.
Рассчитать значения параметров функции аппроксимации заданным методом для каждого набора исходных данных.
Построить исходную и аппроксимирующую функцию на одном графике для каждого опыта используя графические средства языка программирования, либо передать полученные значения в МаthСаd для графического отображения.
2. Теоретическая часть
2.1 Метод выбранных точек
Пусть величина у является функцией аргумента х. Это означает, что любому значению х из области определения поставлено в соответствие значение у. Вместе с тем на практике часто неизвестна явная связь между у и х, т. е. невозможно записать эту связь в виде некоторой зависимости у = f(х). В некоторых случаях даже при известной зависимости у = f(х) она настолько громоздка (например, содержит трудно вычисляемые выражения, сложные интегралы и т. п.), что ее использование в практических расчетах затруднительно.Таким образом, с точки зрения экономии времени и средств мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра у при любом значении (из некоторой области) определяющего параметра х, поскольку точная связь у = f(х) неизвестна.
Этой цели и служит задача о приближении (аппроксимации) функций: данную функцию f(х) требуется приближенно заменить (аппроксимировать) некоторой функцией φ(х). так, чтобы отклонение (в некотором смысле) φ(х). от f(х) в заданной области было наименьшим. Функция у(х) при этом называется аппроксимирующей.
При аналитическом или численном методах расчета нелинейных электрических цепей как в установившемся , так и в переходном режимах используется аналитическая аппроксимация характеристик нелинейных элементов этих цепей.Аппроксимация заключается в определении тем или иным способом аналитической зависимости (формулы) между электрическими переменными, описывавшими данный элемент, приближенно, но с заданной степенью точности, изображающей реальную ( экспериментальную) характеристику элемента, заданную графически или таблично.
По методу выбранных точек коэффициенты функции апроксимации вычисляются из условия точного совпадения аппроксимирующей (приближенной) и аппроксимируемой (точной) характеристик в заранее заданных (выбранных) точках.
Для каждой точки, в которой аппроксимируемая характеристика совпадает с аппроксимирующей составляется уравнение определяемое видом аппроксимирующей функции. Порядок системы уравнений равен количеству неизвестных параметров аппроксимирующей функции. После решения данной системы находят параметры.
2.1 Метод Крамера
Один из самых распространенных методов решения системы линейных уравнений – метод Крамера.
Рассмотрим систему n линейных уравнений с n неизвестными
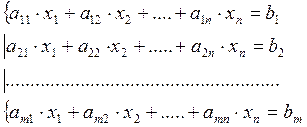
Матрица А – основная матрица системы
А=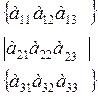
Из соотношения ![]() получаем
получаем
![]() =
= ![]() *
* 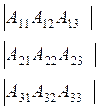 *
*![]()
Отсюда, проведя преобразования, получим
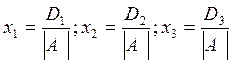 (А)
(А)
Где ![]() - это определитель
матрицы, полученной путем перестановки столбца b c i-ым столбцом
матрицы А.
- это определитель
матрицы, полученной путем перестановки столбца b c i-ым столбцом
матрицы А.
Формулы А называются формулами Крамера.
ПРИМЕЧАНИЕ: если определитель системы отличен от нуля, то она имеет одно единственное решение, определяемое формулами Крамера (А).
3. Системное и техническое обеспечение ЭВМ
Для работы с данной программой необходимо следующее системное и программное обеспечение ЭВМ:
1. Минимальный объем оперативной памяти 2 Мб.
2. Минимальный объем жесткого диска 512 Мб.
3. Процессор не ниже Intel 80286.
4. Операционная система Windows 95 и выше.
5. Любой графический монитор.
6. Клавиатура.
7. Дисковод.
4.Описание математической модели
Аппроксимирующая функция задана в виде
![]()
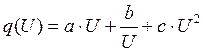 (1)
(1)
Необходимо рассчитать значения коэффициентов a,b,c методом выбранных точек.
Для того чтобы рассчитать коэффициенты нужно выбрать точки из таблицы описывающей аппроксимируемую функцию. Каждому точке будет соответствовать значение заряда и напряжения.
Так как для расчета 3 коэффициентов нужно сформировать 3 уравнения, то нужно выбрать из таблицы 3 точки и подставить значения соответствующие каждой точке в уравнение (1).
Полученную систему уравнений
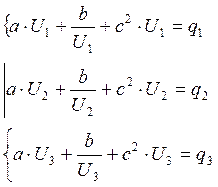
решаем методом Крамера. В результате решения получаем вектор коэффициентов a,b,c.
5.Описание исходных данных
Исходными данными являются зависимости заряда емкости q(U) от приложенного к ней напряжения U, заданные таблично.
Аппроксимируемая функция задана таблицей точек :
|
q(U) |
0,18 |
0,3 |
0,38 |
0,42 |
0,455 |
0,469 |
0,48 |
0,495 |
0,51 |
0,535 |
0,55 |
0,56 |
0,57 |
0,58 |
|
U |
0,5 |
1 |
1,6 |
2 |
2,5 |
2,8 |
3 |
3,5 |
4 |
5 |
6 |
7 |
8 |
9 |
Проведем 3 опыта по аппроксимации функции, предполагая, что в каждом опыте точки в которых аппроксимируемая характеристика совпадает с аппроксимирующая разные(т.е. из таблицы в каждом опыте мы должны брать 3 набора разных точек).
6. Анализ полученных результатов
Результатами расчетов являются значения коэффициентов а также
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.