Граничные условия электродинамики, поля на границах раздела сред. Элементарный электрический вибратор. Уравнения Гельмгольца для векторов поля

1.49) Граничные условия электродинамики, поля на границах раздела сред Пусть над плоской бесконечной поверхностью раздела однородных изотропных сред с параметрами  и  расположен под некоторым углом к поверхности раздела плоский лист синфазного электрического тока (рис. 1а). Необходимо найти возбуждаемое электромагнитное поле, удовлетворяющее уравнениям Максвелла, граничным условиям на поверхности раздела сред и условиям излучения.

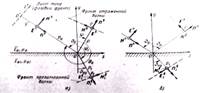
Введем декартову систему координат так, чтобы плоскость xOzсовпала с поверхностью раздела (рис. 1,а). На поверхность раздела сред падает плоская электромагнитная волна. Вектор Пойнтинга ее направлен под углом ν₀ к нормали к поверхности раздела (рис. 1,а). Угол ν₀ называется углом падения волны.

Вектор  перпендикулярен плоскости падения, поэтому эту волну называют нормально поляризованной плоской волной. Поскольку вектор  параллелен поверхности раздела сред, эту волну часто называют горизонтально поляризованной волной.

Полное поле в верхнем полупространстве (y≥0) является наложением падающего и отраженного полей, . Полное поле , в нижнем полупространстве (y≤0) равно вторичному (прошедшему или преломленному) полю, поэтому

(1)

Вектор  параллелен оси х. Поэтому , . Поскольку , то. На поверхности раздела сред необходимо выполнение граничных условий

(2) Тогда

 (3)

 (4) Подставляя эти выражения в (2), получаем граничные условия для составляющих векторных потенциалов

(5)

(6)

Функции  удовлетворяют однородному уравнению Гельмгольца, а  – неоднородному. Эти условия составляют граничную задачу.

2.50) Элементарный электрический вибратор. Элементарным электрическим вибратором называют прямолинейный излучатель, длина которого много меньше длины волны возбуждаемого поля, а модуль и фаза линейной плотности электрическою тока распределены по длине вибратора равномерно (рис. 1,a). Реализовать на практике распределение тока, близкое к равномерному, можно с помощью диполя Герца, представляющего собой два металлических шара, соединенных тонким проводом, к разрезу провода подсоединен, например с помощью двухпроводной линии, источник э. д. с. (рис. 1,б). Длина диполя много меньше длины волны излучаемого поля. Если напряжение в разрезе, создаваемое с помощью источника э. д. с, менять во времени по гармоническому закону, то заряды q^Э(t) на шарах тоже меняются во времени по гармоническому закону. Распределение модуля и фазы электрического тока по длине диполя из-за малой его длины является близким к равномерному. Длина разреза Δ намного меньше длины диполя L, и поэтому можно считать, что провод непрерывен. Таким образом, диполь Герца является физической моделью элементарного электрического вибратора.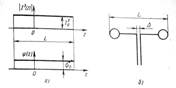

3.51) Уравнения Гельмгольца для векторов поля. Уравнения Гельмгольца для векторов поля имеют вид:

 (14)

Здесь  и — векторные функции сторонних электрических и магнитных токов:

Вместо векторных потенциалов используют вспомогательные функции  и  — комплексные амплитуды векторов Герца для электрических и магнитных токов, связанные с комплексными амплитудами векторных потенциалов:  (15)

Получаем векторные уравнения Гельмгольца для  и :  

4.52) Поляризация плоских волн. Под поляризацией понимают закон изменения направления и величины вектора напряженности электрического поля в данной точке пространства за период колебания. Взяв за основу падающую волну, определим возможные случаи поляризации плоских волн. На основании соотношений запишем следующие выражения для составляющих поля падающей волны в комплексном виде:

Постоянные A₁ и B₁ могут быть комплексными величинами, т. е.

В среде с потерями коэффициент распространения является комплексным, вследствие чего составляющие поля записываются в виде

Переходя от комплексных амплитуд к мгновенным значениям, получаем

 Запишем уравнение кривой второго порядка в координатах y=E_y(t) и x=E_x(t)

 (5) Таким образом, в общем случае конец вектора  перемещается по кривой второго порядка. В аналитической геометрии показывается, что характер этой кривой определяется знаком детерминанта:  (6)

Если детерминант больше нуля, то кривая представляет собой эллипс