Найти вероятность того, что за время t = 3 минут поступят: а) хотя бы один вызов; б) ровно10 вызовов; в) не менее 10 вызовов.
Решение
а) λ =5, m ≥ 1. Событие A – поступило не менее 1 вызова (≥ 1) и событие B - поступило менее 1 вызовов (<1, т.е. m = 0) являются противоположными событиями, поэтому сумма их вероятностей равна 1. Таким образом вероятность события A,
P(A) = 1 – P(B) =1- Р(<1) =1
– P(0) = 1- p3(0) =1 – (5![]() 3) 0e-5
3) 0e-5![]() 3/0! =1 - 0,0000003059 =0,999999694;
3/0! =1 - 0,0000003059 =0,999999694;
б) λ = 5, pt(m) = p3(10) = (5![]() 3)10e-5
3)10e-5![]() 3/10! = 0.0486
3/10! = 0.0486
в) Событие A – поступило не менее 10 вызовов (≥ 10) и событие B - поступило менее 10 вызовов (<10) являются противоположными
событиями, поэтому сумма их вероятностей равна 1. Таким образом, вероятность
события A, P(A) = 1 – P(B) =
1- P(<10) = 1 - 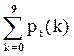 =
=
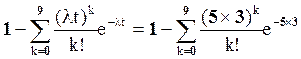 = 1 – 0,06985= 0.93015
= 1 – 0,06985= 0.93015
Примечание. В приведённых вычислениях необходимо суммировать 10 членов ряда, эту
рутинную операцию можно избежать, если воспользоваться таблицей случайной пуассоновской
величины, содержащейся в программе ![]() Excel
ПК: «ПУАССОН (9;15;1) = 0,06985366070».
Excel
ПК: «ПУАССОН (9;15;1) = 0,06985366070».
Пример 2.
Среднее число самолётов, прибывающих в аэропорт за 1 час, равно 3. Найти вероятность того, что за 4 часа прибудут а) 8самолётов; б) не менее 12 самолетов. Поток прибытия предполагается простейшим, пуассоновским.
Решение
а) λ = 3 , pt (m) = p4(8) = (3![]() 4)8e-3
4)8e-3![]() 4/8! = 0.0655
4/8! = 0.0655
б) P(≥12) = 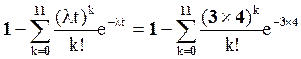 = 1-0,4615973 = 0.5384027
= 1-0,4615973 = 0.5384027
Распределение интервала времени T между произвольными двумя соседними событиями простейшего потока.

Рис.4.
Так как вероятность того, что на промежутке времени t не появится ни одного из последующего события (2.1.2), равна:
![]() , то вероятность
противоположного события, т.е. функция распределения случайной величины T, есть:
, то вероятность
противоположного события, т.е. функция распределения случайной величины T, есть:
![]() .
(2.1.3)
.
(2.1.3)
Плотность распределения случайной величины есть производная от её функции распределения, т.е.
![]() (2.1.4)
(2.1.4)
Распределение, задаваемое плотностью вероятности (2.1.4) или функцией распределения (2.1.3) является показательным (экспоненциальным)
Таким образом, случайная величина T – интервал времени между двумя произвольными соседними событиями имеет показательное распределение, для которого математическое ожидание равно среднему квадратическому значению T (см.§2.1.1):
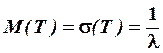
Отметим важнейшее свойство показательного распределения (присущее только этому распределению), которое состоит в следующем:
если промежуток
времени, распределённый по показательному закону, уже длится некоторое время ![]() ,
то это никак не влияет на закон распределения оставшейся части промежутка (T –
,
то это никак не влияет на закон распределения оставшейся части промежутка (T – ![]() ): он будет таким же, как и закон распределения всего промежутка T.
): он будет таким же, как и закон распределения всего промежутка T.
Другими словами, для интервала времени T между двумя последовательными соседними событиями потока, имеющего показательное распределение, любые сведения о том, сколько времени протекал этот интервал, не влияет на закон распределения оставшейся части. Это свойство показательного закона представляет собой, по сути дела, другую формулировку для «отсутствия последействия» – основного свойства простейшего потока.
Приведём ещё одну важную характеристику простейшего потока, которую мы будем использовать при выводе и использовании уравнений Марковских процессов. Для простейшего потока с интенсивностью λ вероятность попадания на элементарный (малый) отрезок времени Δt хотя бы одного события потока (противоположное событие – ноль событий) равна согласно (2.1.2):

![]() (2.1.5)
(2.1.5)
Примечание. Отметим, что выражение (2.1.5) получено с учётом в разложении функции e-λΔt в ряд Маклорена по степеням Δt только двух членов ряда, и это приближение будет тем точнее, чем меньше Δt.
Подведём итог.
Использование моделей простейших потоков событий в качестве входных и выходных процессов в СМО определяется свойствами таких потоков:
1) стационарность – постоянное число событий в единицу времени;
2) отсутствие последействия – независимость числа событий после любого момента времени от числа событий до него;
3) ординарность – практическая невозможность одновременного наступления нескольких событий,
позволяющих применение аналитических методов теории случайных процессов при построении и анализе математических моделей СМО.
§2.1.3. Основные категории теории массового обслуживания
Теория массового обслуживания (или теория очередей) строит модели процессов, для которых характерна следующая структура: в систему массового обслуживания (СМО) в случайные моменты времени поступают заявки или требования, образующие входной поток СМО. Это могут быть линии связи, приемные или отправные пункты (терминалы), подъездные пути, взлётно-посадочные полосы, технологические линии, ремонтные бригады и т. п. Если есть свободные каналы обслуживания, то требования выполняются. Если все каналы обслуживания заняты, то требование становятся в очередь по определённому правилу или без обслуживания покидают систему. Выполненные требования (обслуженные заявки) образуют выходной поток СМО.
В настоящее время теоретически наиболее разработанными являются модели СМО, в которых поток требований является простейшим, пуассоновским, с интенсивностью λ, определяющим среднее число требований (заявок), поступающих в единицу времени на вход СМО.
СМО состоит из определённого числа обслуживающих единиц – каналов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.