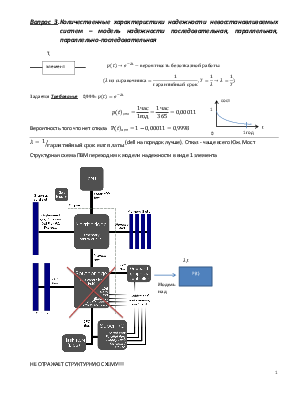


Вопрос 3.Количественные характеристики надежности невосстанавливаемых систем – модель надежности последовательная, параллельная, параллельно-последовательная
T,
![]()


![]() (dell на порядок лучше). Отказ - чаще всего
Юж. Мост
(dell на порядок лучше). Отказ - чаще всего
Юж. Мост
Структурная схема ПВМ переходим к модели надежности в виде 1 элемента
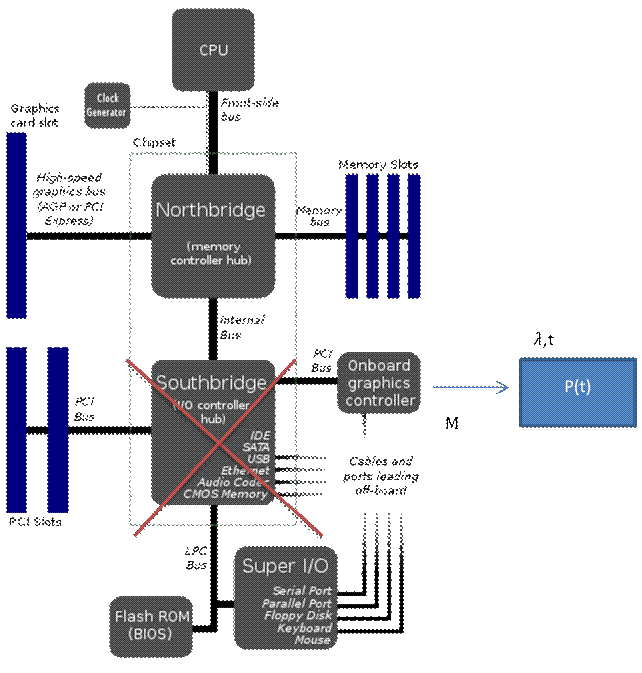
НЕ ОТРАЖАЕТ СТРУКТУРНУЮ СХЕМУ!!!
• Предполагаем, что система состоит из взаимосвязанных элементов, надежность которого известна, структурная схема системы задана (отражает работу системы)
• Элементы в структурной схеме не зависят друг от друга – надежность каждого элемента не зависит от других
Последовательная модель надежности – модель, в которой n элементов соединены последовательно в смысле надежности (отказ одного любого эл вызывает отказ всей системы)
Найти:
вероятность безотказной работы для последовательной модели надежности P(t), ![]() дано
дано
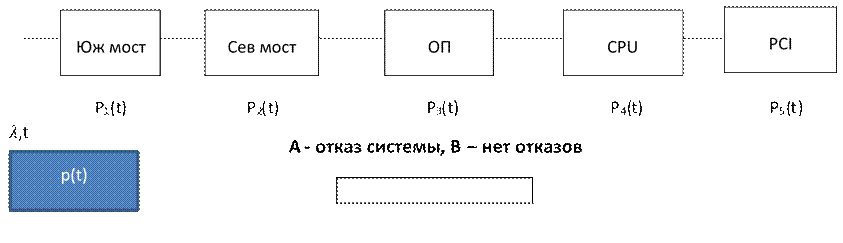
Перейдем к событию, что в системе нет отказов (В)
![]()
![]()
![]()
( ) ⋂ ∏ ( ) ∏ (∑ ) ( )
Т.о. интенсивности отказов при последовательной модели складываются. Средняя наработка на отказ при последовательной модели:
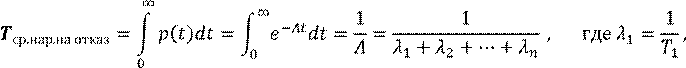
![]()
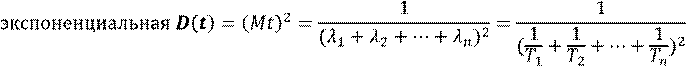
Замечание 1. Можно найти приближенную формулу для вычисления вероятности отказа.

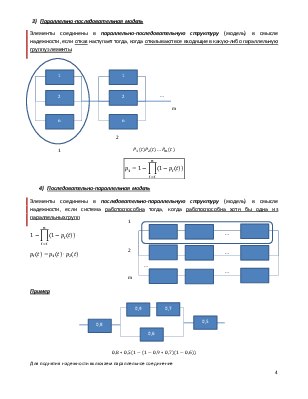
n-элементов соединены параллельно в смысле надежности, если отказ в системе наступает тогда, когда отказывают все входящие в систему элементы
• все элементы независимы
• заданы вероятности безотказной работы (p)
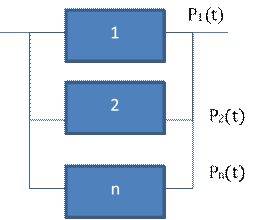 Найти: вероятность безотказной работы
для параллельного соединения.
Найти: вероятность безотказной работы
для параллельного соединения.
![]()
( ) (∏ ( )) ∏ ( ) ∏

( )( )
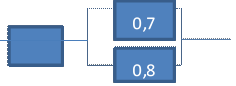
Пример p1=0,7, p2=0,8, p3=0,9
• Последовательное p=0,7*0,8*0,9=0,504
•
![]() Параллельное q=0,3*0,2*0,1=0,0006 p=0,994
Параллельное q=0,3*0,2*0,1=0,0006 p=0,994
• Найдем среднее время наработки на отказ, когда имеем n элементов и все они одинаковые
![]() ) ]
| | ∫[ ] ∫ ∫ ( ) ∫[ (
) ]
| | ∫[ ] ∫ ∫ ( ) ∫[ (
![]()
![]() ∫(
) (
∫(
) ( ![]() )
)
![]()
( )
 ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( )
![]()
Найти дисперсию наработки на отказ!!!
![]()
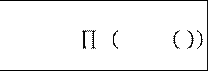
![]()
![]()
![]()
![]()
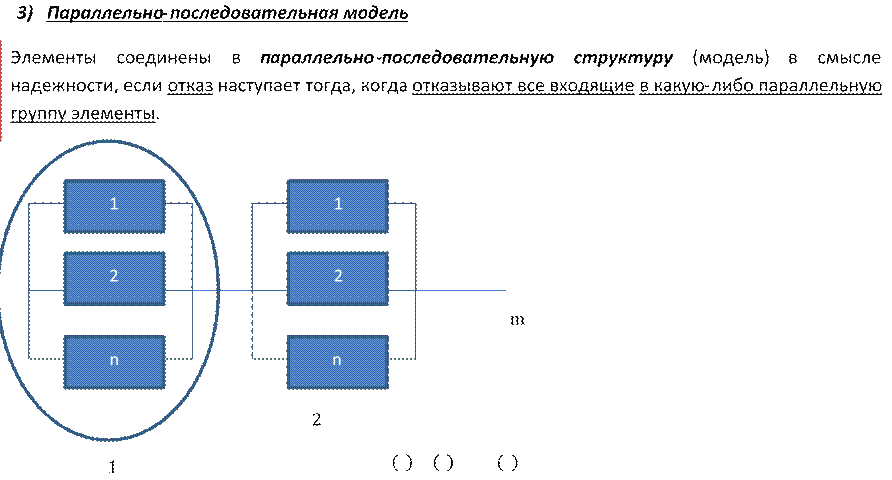
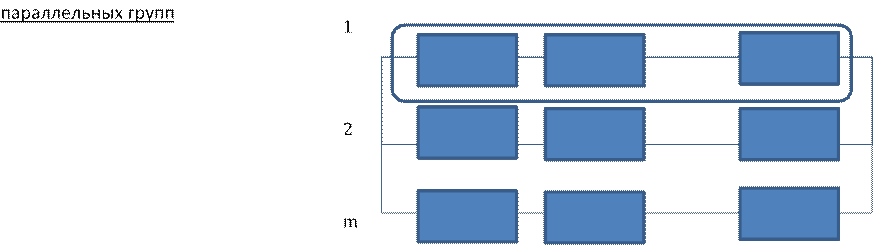
![]() Элементы
соединены в последовательно-параллельную структуру (модель) в
смысле надежности, если система работоспособна тогда, когда работоспособна
хотя бы одна из
Элементы
соединены в последовательно-параллельную структуру (модель) в
смысле надежности, если система работоспособна тогда, когда работоспособна
хотя бы одна из
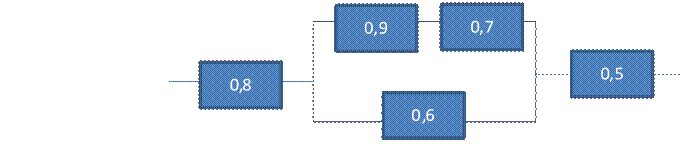
![]()
Для поднятия надежности включаем параллельное соединение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.