2.2.18 Математическая постановка задачи проектирования АЭИС как задачи многокритериальной оптимизации. Методика решения задачи многокритериальной оптимизации Многокритериальная оптимизация.
Показатели качеств: время, стоимость, надежность комплекса технических средств, достоверность информации.
Линейное программирование – выполнение 4-х пунктов: целевая функция линейна, ограничения линейны, переменные неотрицательные.
Целочисленное (дискретное) программирование – целевая функция линейна, ограничения линейны, переменные неотрицательные, некоторые или все переменные обязаны иметь целочисленные значения.
Нелинейное программирование –целевая функция и ограничения нелинейны. На переменные ограничения не ставятся.
Квадратичное программирование – часть нелинейного программирования. Максимум могут иметь второй порядок.
Динамическое программирование – самое сложное, с решением по ситуации.
Стохастическое программирование – когда события носят вероятностный характер.
Теория игр – нулевая сумма. Если применять элементы статистики, то и теория статистическая.
Многокритериальные задачи – минимум два показателя качества.
Многокритериальные задачи – минимум два показателя качества.
![]()
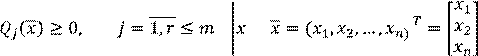
![]()
![]()
Найти
![]() ,
, ![]()
![]()
Qj-частные критерии
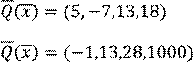
имеют разную цену и диапазон изменения.
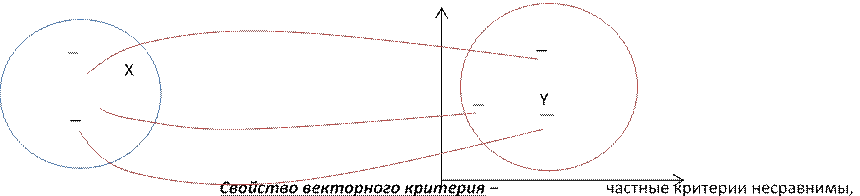
Частные критерии противоречивы. Векторные критерии не выражаются количественно. Нормирование показательных величин следует использовать в этом случае (чтобы все критерии были безразмерные, в одном диапазоне, придать один смысл оптимизации). Когда объединение проходится с помощью суммы, свертка называется аддитивная.
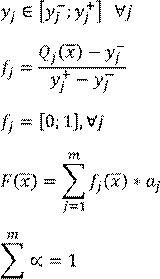
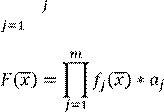
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.