Схема суммирующего параллельного счетчика на D-триггерах с коэффициентом счета равным 24

D4  Q5Q4Q3Q2Q1Q4Q3Q4Q2Q4Q1

 ((Q5  Q4)  (Q3 Q2  Q1))  (Q4  Q3)  (Q4  Q2)  (Q4  Q1);

D3  Q3Q1Q3Q2Q3Q2Q1 (Q3  Q1)  (Q3 Q2)  (Q3 Q2  Q1);

D2  Q2Q1Q2Q1 (Q2Q1) (Q2Q1)  (Q2  Q1)  (Q2  Q1); D1 Q1.

где слагаемое из функции возбуждения D4 (так как в базисе ИЛИ-НЕ нету элементов

ТТЛ более чем на 4 входа, а данное слагаемое содежит 5 элементов): Q5Q4Q3Q2Q1 преобразовывается следующим образом:

Q5Q4Q3Q2Q1(Q5Q4)(Q3Q2Q1) (Q5Q4)(Q3Q2Q1)(Q5Q4)(Q3Q2Q1)

(Q5Q4)(Q3Q2Q1)

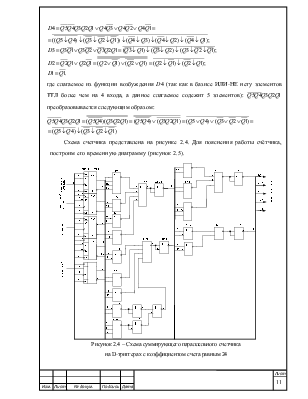
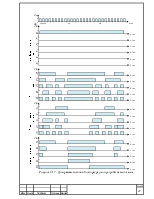
Схема счетчика представлена на рисунке 2.4. Для пояснения работы счётчика, построим его временную диаграмму (рисунок 2.5).

Рисунок 2.4  Схема суммирующего параллельного счетчика 

на D-триггерах с коэффициентом счета равным 24

11

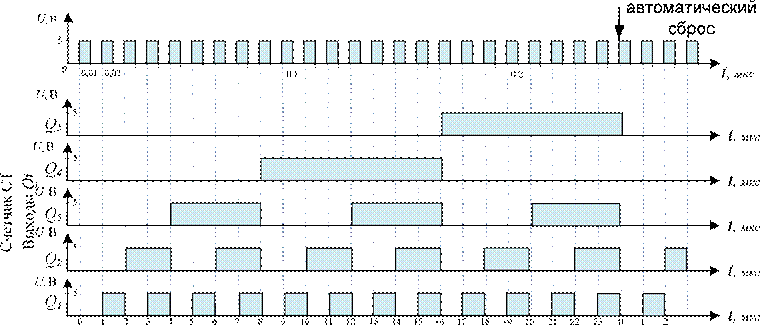
Рисунок 2.5 – Временная диаграмма работы суммирующего параллельного

счетчика с коэффициентом счета равным 24

12

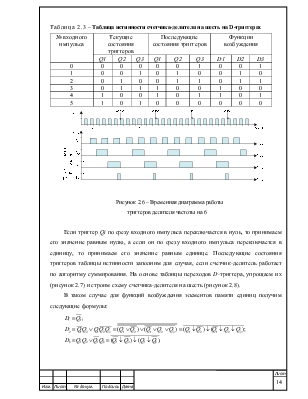
Таблица 2.3 – Таблица истинности счетчика-делителя на шесть на D-триггерах

Рисунок 2.6 – Временная диаграмма работы  триггеров делителя частоты на 6

Если триггер Qi по срезу входного импульса переключается в нуль, то принимаем его значение равным нулю, а если он по срезу входного импульса переключается в единицу, то принимаем его значение равным единице. Последующие состояния триггеров таблицы истинности заполним для случая, если счетчик-делитель работает по алгоритму суммирования. На основе таблицы переходов D-триггера, упрощаем их (рисунок 2.7) и строим схему счетчика-делителя на шесть (рисунок 2.8).

В таком случае для функций возбуждения элементов памяти единиц получим следующие формулы: 

D1 Q1 ; 

               2                                                                                                                              1 2

D₃ Q₁Q₂ Q₁Q₃  (Q₁ Q₂)  (Q₁ Q₃).

14

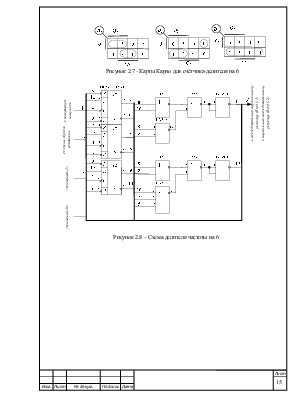
Рисунок 2.7 - Карты Карно для счётчика-делителя на 6

Рисунок 2.8 – Схема делителя частоты на 6

15

2.5 Синтез последовательного-параллельного регистра

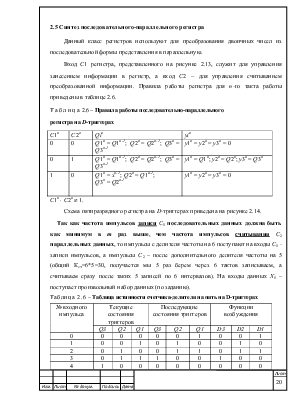
Данный класс регистров используют для преобразования двоичных чисел из последовательной формы представления в параллельную. 

Вход C1 регистра, представленного на рисунке 2.13, служит для управления занесением информации в регистр, а вход C2  для управления считыванием преобразованной информации. Правила работы регистра для n-го такта работы приведены в таблице 2.6. 

Т а б л и ц а  2.6 – Правила работы последовательно-параллельного  регистра на D-триггерах

C1ⁿ  C2ⁿ  1. 

Схема пятиразрядного регистра на D-триггерах приведена на рисунке 2.14. 

Так как частота импульсов записи C₁ последовательных данных должна быть

как минимум в m раз выше, чем частота импульсов считывания C₂ параллельных данных, то импульсы с делителя частоты на 6 поступают на входы С₁ - записи импульсов, а импульсы С₂ – после дополнительного делителя частоты на 5 (общий К_сч=6*5=30, получается мы 5 раз берем через 6 тактов записываем, а считываем сразу после таких 5 записей по 6 интервалов). На входы данных Х₁ – поступает произвольный набор данных (по заданию).

Таблица 2.6 – Таблица истинности счетчика-делителя на пять на D-триггерах

20

2.6 Синтез устройства вычитания

Вычитание двух чисел обычно сводится к операции сложения: 

                                               ^{n                   n                    n}                                                                                                                    n

DABA(2 B)2 ,где 2 BB1 дополнение В до числа 2 , которое легко получить без помощи специальных схем, использующих вычитание.

Таким образом, вычитание можно осуществить инвертируя число B, суммируя полученный результат с А и еще с одной 1 и вычитая 2ⁿ. Вычитание достигается весьма просто – путем инверсии сигнала переноса.

Операцию сложения можно осуществить при помощи двоичных сумматоров