Для определения приращения (производной от значения функции в конце шага) в начале значение функции в конце шага определяют ориентировочно.
1. ![]()
2. ![]()
3. ![]()
Начальные условия: h, R, L, C, E, I = 0, Q = 0, dI0 = 0, dQ0 = 0.
2.
![]()
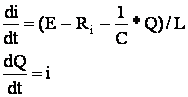
![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]()
3.
![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]()
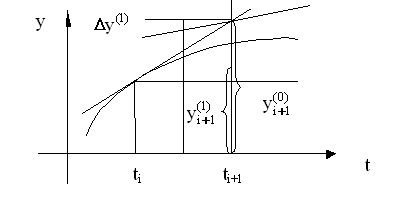
МЕТОД ЭЙЛЕРА-КОШИ С ИТЕРАЦИЕЙ
![]()
![]()
R ~ h3
Если две итерации, то имеем метод Эйлера-Коши второго порядка. Выполняя итерации, мы приближаемся к истинному значению функции.
 |
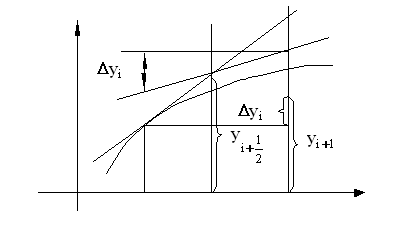
МОДИФИЦИРОВАННЫЙ МЕТОД ЭЙЛЕРА-КОШИ
![]()
![]()
 |
МЕТОД ТРАПЕЦИЙ
Приращение на шаге вычисляется как среднеарифметическое приращений, полученных прямым и обратным методом Эйлера.
![]()
![]()
![]()
МЕТОД БАШАРИНА
![]()
![]()
![]()
![]()
![]()
![]()
ПРИМЕР
![]()
![]()
В методе Башарина приращения каждой последующей функции системы уравнений вычисляется с учетом приращений ранее вычисленных функций.
ПРОБЛЕМА ЭНЕРГЕТИЧЕСКОГО БАЛАНСА
ПРИ ЧИСЛЕННОМ ИНТЕГРРОВАНИИ
Уравнения законов электротехники получены исходя из закона сохранения энергии:
![]() (1)
(1)
WL – энергия электромагнитного поля в индуктивности;
WС – энергия электромагнитного поля в конденсаторе;
WR – энергия тепловых потерь в резисторе;
WЕ – энергия источника питания.
Продифференцируем по времени и получим уравнение баланса мощностей:
![]()
![]() (2)
(2)
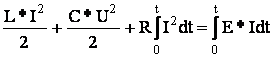
Возьмем производную:
![]() (3)
(3)
![]()
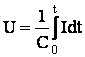
![]()
Полученное выражение подставляем во второй закон Кирхгофа и делим на I:
![]()
Проблема энергетического баланса возникает из-за появления ошибки ξ:
![]() (4)
(4)
Эта ошибка не отражается в уравнении баланса мощности (2) и в уравнении (3), т.к. производная от постоянной величины равна 0.
При решении уравнений (2) и (3) с некоторой постоянной ошибкой ошибка по энергии в уравнении (4) будет меняться, т.е. увеличиваться, т.к. интеграл от постоянной величины есть линейная функция. Таким образом, ошибки численных методов приводят к нарушению энергетического баланса и накоплению ошибки по энергии.
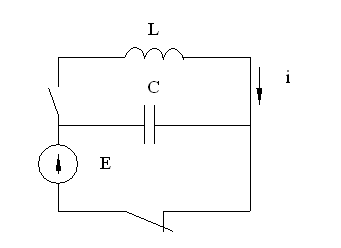 |
![]()
![]()
НУ: i = 0, U = U0 = E.
![]()
![]()
![]()
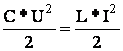
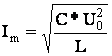
![]()
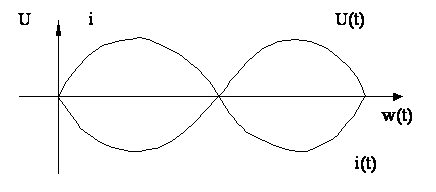 |
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим энергию в начале и конце шага интегрирования и определим ошибку по энергии на шаге.
Энергия в начале шага:
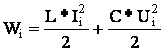
Энергия в конце шага:
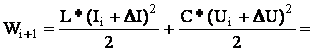
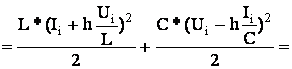
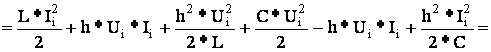
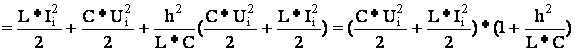
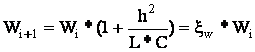
ξw – ошибка по энергии на шаге.
ξw ~ h2
Таким образом, вводя коррекция по энергии на каждом шаге интегрирования, мы можем скорректировать погрешность (т.е. уменьшить), вносимую численным методом Эйлера. Это прямой метод.
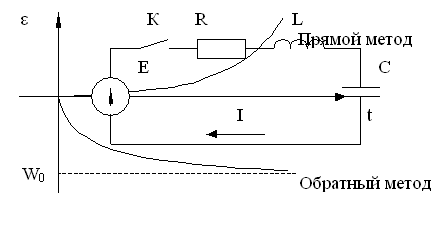
Обратный метод
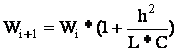
εW < 0
 |
![]()
 |
![]()
 |
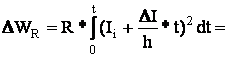
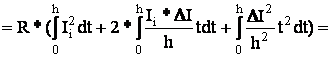
![]()
Энергия теряемая:
![]()
Энергия выделенная источником:
![]()
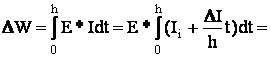
![]()
![]()
Точность метода дифференциальных уравнений.
Типы ошибок
Полная ошибка дифференциального уравнения на i шаге складывается из ошибки вычисления, которая определяется разрядной сеткой машины и реализации нематематических операций с помощью арифметических действий, и ошибки накопления, которая равна полной ошибки на предыдущем шаге.
![]()
где ![]() -
ошибка аппроксимации;
-
ошибка аппроксимации;
![]() -
ошибка вычислений;
-
ошибка вычислений;
![]() -
ошибка накопления.
-
ошибка накопления.
Ошибку можно оценить, разложив функцию в ряд Тейлора:
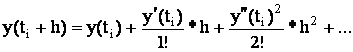
![]()
![]()
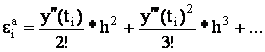
![]() ~ h2
~ h2
АНАЛИЗ СТАТИЧЕСКИХ РЕЖИМОВ. МЕТОДЫ РЕШЕНИЯ
СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
По окончании переходного процесса в динамическом объекте он переходит в определённое устойчивое состояние (статический режим). Статический режим можно рассчитать, интегрируя исходную систему обыкновенных дифференциальных уравнений на большом интервале времени.
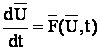 (1)
(1)
Этот метод называется методом установления.
В статическом режиме производные переменных по времени равны 0 и отсутствуют меняющиеся по времени внешние воздействия.
![]() (2)
(2)
Таким образом, одновариантный анализ статических режимов динамических объектов, описываемых системой уравнений (1), сводится к решению системы алгебраических уравнений (2) n-порядка.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
![]() АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ
ГАУСА
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ
ГАУСА
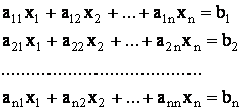
В матричной форме:
![]()
где ![]() -
матрица коэффициентов размерностью n x n;
-
матрица коэффициентов размерностью n x n;
![]() -
n-мерный вектор переменных;
-
n-мерный вектор переменных;
![]() -
n-мерный вектор свободных членов.
-
n-мерный вектор свободных членов.
МЕТОД ГАУСА
Относится к прямым (точным) методам.
Основан на последовательном исключении неизвестных до тех пор, пока не останется только одно уравнение с одной неизвестной в левой части. Затем это уравнение решается, т.е. находится неизвестная. Полученное значение неизвестной подставляется в предыдущее уравнение с двумя неизвестными и находится следующая неизвестная и т.д.
Таким образом, вычислительный процесс при использовании метода Гауса может быть разбит на два этапа:
- прямой ход;
- обратный ход.
1. i = 1…n, j
= 1…n, aij ,![]() , bi ,
, bi ,![]() .
.
2. Прямой ход.
В результате выполнения прямого хода матрица коэффициентов преобразуется к треугольному виду. Выполняется за n – 1 стадию и на каждой k стадии исключается очередная неизвестная Хк.

где i – порядковый номер строки;
j – порядковый номер столбца.
3. Обратный ход.
Состоит из n – 1 стадий.
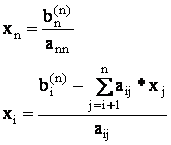
ПРИМЕР

1. Прямой ход.
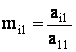
m21 = 2 / 2 = 1; m31 = 4 / 2 = 2; m41 = 6 / 2 = 3.
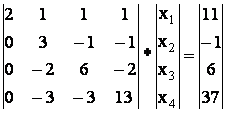
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.