Понятие алгоритма. Блок-схема алгоритма. Численные методы вычисления определённых интегралов

ПОНЯТИЕ АЛГОРИТМА.

БЛОК-СХЕМА АЛГОРИТМА

Алгоритм – точное предписание, определяющее содержание и порядок действий, которые необходимо выполнить над исходными и промежуточными данными для получения конечного результата при решении задач определённого типа.

ОСНОВНЫЕ ЭЛЕМЕНТЫ БЛОК-СХЕМ АЛГОРИТМА

 

- начало или конец, прерывание

 

- программный ввод и вывод данных

 

- ввод данных с клавиатуры

 

- вывод данных на экран

 

- вывод данных на печать

 

- условный оператор

 

- блок модификации (задание параметров цикла)

 

- блок вычислений

ЧИСЛЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ

ЗАДАЧА

Вычислить определённый интеграл:  .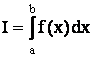

В случае, если данный интеграл нельзя представить в виде комбинации табличных интегралов, то прибегают к численным методам решения интеграла. Исходят из того, что определённый интеграл – это есть некоторая площадь, ограниченная кривой графика функции f(x) и пределами a и b.

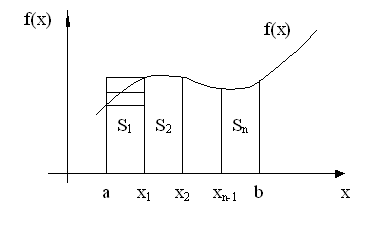На каждом из интервалов заменяют функцию f(x) некоторой функцией F(x), причём f(x) ≈ F(x).

F(x) – кусочная функция (линейная или нелинейная).

1. Метод  прямоугольников.

При этом методе функция на каждом элементарном интервале заменяется постоянной величиной равной значению функции в начале, конце или середине интервала. Поэтому различают метод внутренних, внешних или средних прямоугольников.

Для метода внутренних прямоугольников:

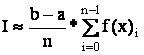
где  - шаг интегрирования.

Для метода внешних прямоугольников:

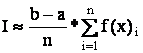
Для метода средних прямоугольников:

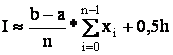
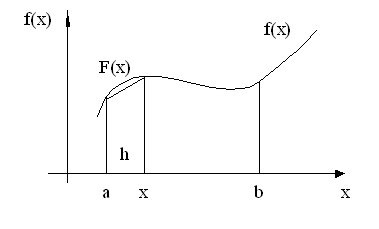
2. Метод трапеций.

При этом методе функция заменяется на каждом интервале линейной функцией, совпадающей с началом и концом.

Численное значение интеграла есть сумма площадей элементарных трапеций:

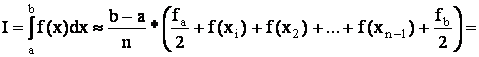
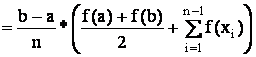
ЗАДАЧА КОШИ. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ.

ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ ЧИСЛЕННЫХ МЕТОДОВ

РЕШЕНИЯ ОБЫЧНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Для моделирования динамики объектов на цифровой ЭВМ математическое описание объекта должно быть проверено в форме Коши, т.е. представлена в виде системы дифференциальных уравнений первого порядка, разрешённых относительно производных:

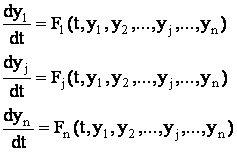        (1)

где y₁,…,y_n – зависимые переменные;

t – независимая переменная.

(1) – математическое описание объекта, записанное в форме Коши.

Любое дифференциальное уравнение высшего порядка можно привести к системе уравнений первого порядка, путём введения дополнительных переменных:

       

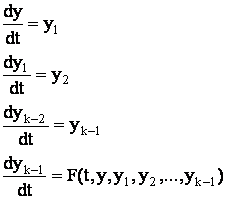
Решаем систему (1) при заданных начальных условиях.

НУ: t = t₀, y₁(t₀) = y₁₀,…, y_j(t₀) = y_j0,…, y_n(t₀) = y_n0.

Обычно t₀ = 0.

Определить: y₁(t), y₂(t),…, y_n(t).

Решается путём численного интегрирования дифференциальных уравнений системы (1) и называется задачей Коши:

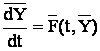
где 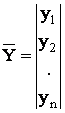 - вектор переменных состояния объекта;

 - вектор - функция

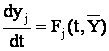
Все численные методы интегрирования системы обычных дифференциальных уравнений основаны на том, что начиная с t₀ меняют независимую переменную t с приращением ∆t.

где h – шаг интегрирования.

Находят последующие значения переменной , начиная с начальных значений  и заканчивая .

Каждое последующее значение зависимой переменной (значение в конце шага):

Приращение переменной на шаге интегрирования определяется исходя из дифференциальных уравнений, представленных в конечно-разностной форме:

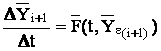
где  - значение функции в некоторой точке ε на (i + 1) шаге, при которой вычисляется значение производной .

Численные методы интегрирования отличаются точкой на шаге интегрирования, в которой берётся производная и количеством ранее определённых значений переменных, которые используются для нахождения приращения.

Если производная берётся в начале шага интегрирования, то такие методы называются явными.

Если производная берётся не в начале шага интегрирования, то такие методы называются неявными. Интегрирование неявными методами осуществляется в виде нескольких итераций на каждом из шагов интегрирования. Количество приближений (итераций) определяет порядок метода.

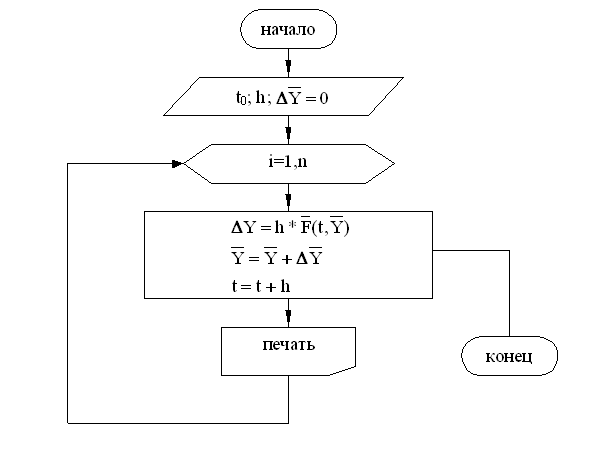
ПРЯМОЙ МЕТОД ЭЙЛЕРА

Прямой метод Эйлера является явным методом и предполагает вычисление приращения функции исходя из производной, взятой в начале шага.

F(t) ≈ f(t)

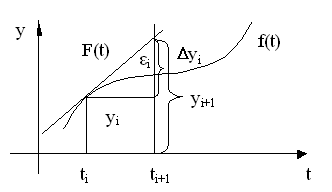.ε_i ~ h²

ПРИМЕР

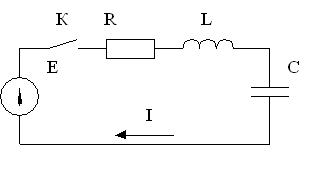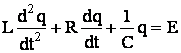
Переход к форме Коши:

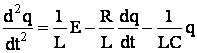
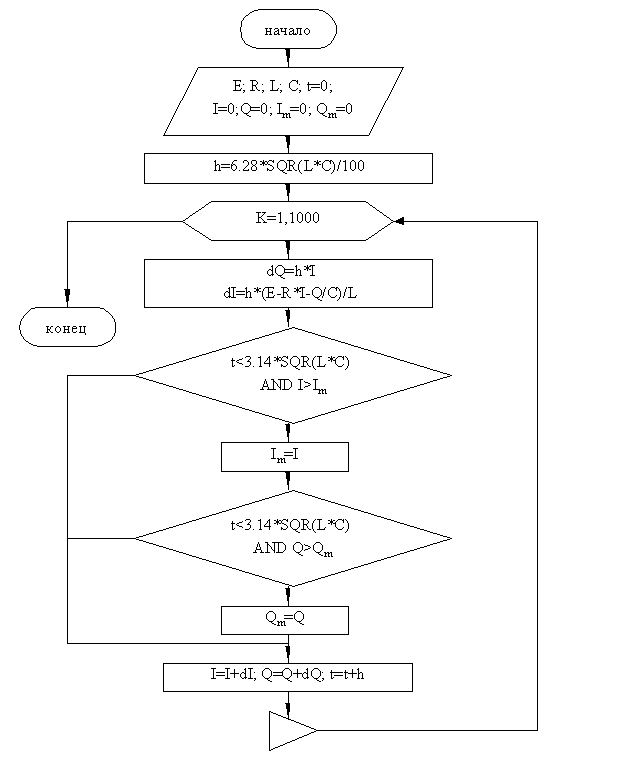Программа

10 CLS: SCREEN 2

20 DATA 500, 100, 0.4, 0.000002

30 READ E, R, L, C

40 I=0: Q=0: t=0: I_m=0: Q_m=0

50 h=6.28*SQR(L*C)/100

60 FOR K=1 TO 1000

70 dQ=h*I

80 dI=h*(E-R*I-Q/C)/L

90 IF t<3.14*SQR(L*C) AND I>I_m THEN I_m=I

100 IF t<3.14*SQR(L*C) AND Q>Q_m THEN Q_m=Q

110 t=t+h: I=I+dI: Q=Q+dQ

120 PSET (20+K, 100-I*20)

130 PSET (20+K, 100-Q*10000)

140 PSET (20+K, 100)

141 PSET (320+I*20, 100-Q*10000)

150 NEXT K

160 FOR j=0 TO 640 STEP 10

170 LINE (0, 0+j)-(640, 0+j)

180 NEXT j

190 FOR M=0 TO 640 STEP 20

200 LINE (0+M, 0)-(0+M, 640)

210 NEXT M

220 ‘I_max=’: I_m: ‘Q_max=’: Q_m

230 END

ОБРАТНЫЙ МЕТОД ЭЙЛЕРА

При обратном методе Эйлера значение функции в конце шага вычисляется как значение функции в начале шага плюс приращение, которое определяется, исходя из производной функции, взятой в конце шага, поэтому метод является неявным.

R ~ h²

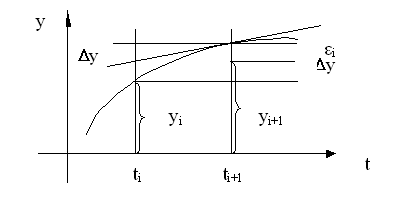Метод является жёстко устойчивым.