Экономико-математические модели. Параметры функций спроса и предложения. Расчет равновесной цены

Министерство образования Российской Федерации

Тульский государственный университет

Кафедра прикладной математики и информатики

Экономико-математические модели

Расчетные работы 1-4.

Выполнил  _____________________

Проверил                           _____________________ 

Тула 2001

Вариант № 17.

Задание № 1.

Построить модель Вальраса, определить количество сделок при которых торговые операции становятся убыточными. Заданы параметры функции спроса D и функции предложения S, начальная цена .

Провести анализ полученного результата и установить, от чего зависит сходимость итерационного процесса регулирования рынка. установить, какие из параметров модели (a, A, b, B) влияют на сходимость, какие не влияют. каким должно быть соотношение влияющих на сходимость параметров модели, чтобы процесс сходился? Влияет ли на факт сходимости начальная цена?

Параметры функций

Спроса D: a = 37   A = 1,8

Предложения S: b = 7   B = 1,5

Начальная цена = 5

Расчет равновесной цены представлен в таблице 1.

Расчет равновесной цены                                                                                      Таблица 1.

1	5	14,5	14,5	12,5
2	12,5	25,75	25,75	6,25
3	6,25	16,375	16,375	11,4
4	11,4	24	24	7,2
5	7,2	17,8	17,8	10,6
6	10,6	22,9	22,9	7,83
7	7,83	18,75	18,75	10,1
8	10,1	22,1	22,1	8,3
9	8,3	19,45	19,45	9,7
10	9,7	21,5	21,5	8,62
11	8,62	19,93	19,93	9,4
12	9,4	21	21	8,9
13	8,9	20,3	20,3	9,2
14	9,2	20,8	20,8	9,0
15	9,0	20,5	20,5	9,1
16	9,1	20,65	20,65	9,083
17	9,083	20,63	20,63	9,095
18	9,095	20,643	20,643	9,0873
19	9,0873	20,631	20,631	9,093
20	9,093	20,64	20,64	9,09

Таким образом, равновесная цена равна 9,09, аналогичное значение получается и по формуле:

.

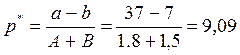Равновесное количество сделок (предложений)  равно 20.

Торговые операции становятся убыточными при количестве сделок 20.

Задание № 2.

По имеющимся исходным данным определить оптимальные значения основных величин, определяющих модель управления товарными запасами, по критерию минимума издержек обращения. Необходимо:

1) составить критерий минимизации издержек обращения при управлении товарными запасами.

2) построить график зависимости издержек обращения от размера партии поставки.

3) найти оптимальные значения величин 

- затраты на хранение товаров за период ;

- величина среднего запаса;

- размер одной партии поставки товара;

- затраты на ввоз (транспортировку);

- число поставок за анализируемый период;

- интервал поставок;

4) написать уравнение и построить график уровня товарных запасов на любой момент времени .

5) проанализировать полученные результаты.

Исходные данные:

Интенсивность продажи товаров  = 1,4  тыс. руб./день

Величина анализируемого периода 15 мес.

Общий объем поставок  за период , =640 тыс. руб.

Затраты на ввоз одной партии товара 13 тыс. руб.

Затраты на хранение единицы товара в течение года 0,87 тыс. руб.

Выполнение:

1)  Критерий минимизации издержек обращения имеет вид: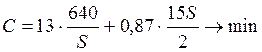

2)  График зависимости издержек от размера партии поставки представлен на рисунке 1.

,   ,  .

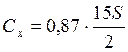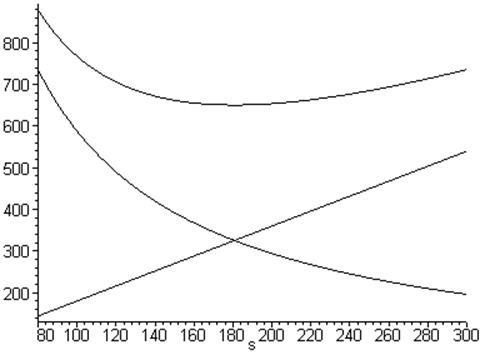
Рис.1. Зависимость издержек от размера партии поставки

3) Оптимальные параметры системы:

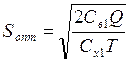=35,7 – размер одной поставки товаров;

232,94 – затраты на хранение товаров за период ;

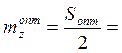17,85 – средний запас текущего хранения;

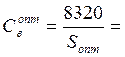233,05 – оптимальные затраты на ввоз;

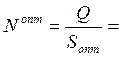17,93 – оптимальное число поставок за период ;

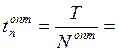0,836 – оптимальный интервал между поставками;

4) Уравнение уровня товарных запасов на любой момент времени имеет вид:

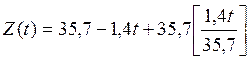, его график представлен на рисунке 2.

 

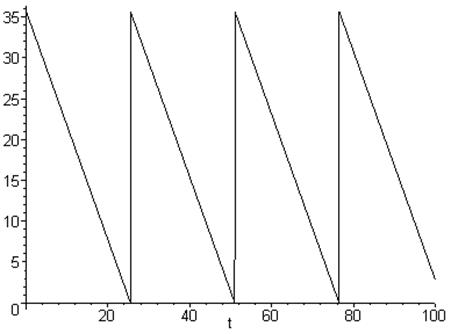
Рис.2. Динамика изменения товарных запасов.

Задание № 3.

Фирма выпустила на рынок три конкурирующих (взаимозаменяемых) изделия. С целью определения спроса на эти изделия произведен опрос покупателей. Оказалось, что из  человек  покупает первое изделие, - второе, - третье. .

Повторный опрос этих же покупателей через неделю показал, что из  человек, покупавших первое изделие , продолжают его покупать,  стали покупать второе изделие, остальные – третье. Из  человек, покупавших второе изделие, продолжают его покупать  человек,  стали покупать первое изделие, остальные – третье. Из  человек, покупавших третье изделие,  человек продолжают его покупать, и - стали покупать соответственно первое и второе.

Определить, какое изделие будет пользоваться наибольшим спросом а) через неделю; б) через две недели; в) через год;

Исходные данные:

180   400    120   95     = 45   80  230  25  60

Решение:

Пусть - вероятность потребности изделия  в начальный момент времени.

.

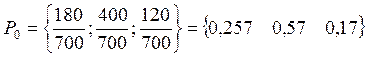Тогда  матрица переходных вероятностей имеет вид:

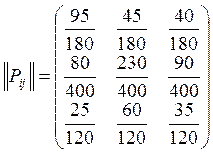 или .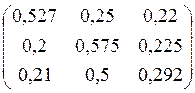

Вероятности покупок изделий через неделю:

= =  ;

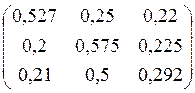Таким образом, через неделю наибольшим спросом будет пользоваться второе изделие.

Через две недели

=

наибольшим спросом  также будет пользоваться второе изделие.

Для определения спроса через год, считаем, что поведение покупателей со временем не меняется. Так как все элементы матрицы перехода положительны, то предельные вероятности потребления изделий существуют и находятся как решение системы линейных уравнений:

 

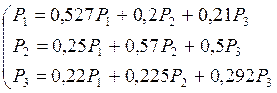
Эта система линейно зависима, заменяя одно из уравнений на нормировочное, получаем решение:

0,3   0,46   

Итак, второе изделие и через год остается самым популярным.

Задание № 4.

Предприятие состоит из двух основных цехов и одного вспомогательного, каждый из которых выпускает один вид продукции. Известны расходные коэффициенты (прямые затраты) единиц продукции