Работа с редакторами ввода математических формул. Выполнение расчетов с использованием вычислительного табличного редактора MicrosoftWord, страница 3

Структура вычислительной таблицы зависит, прежде всего, от характера математического выражения, для вычисления которого она составляется. Например, для определения сумм для системы нормальных уравнений метода наименьших квадратов вида:

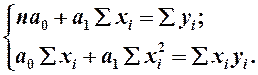
Исходные данные для этой системы уравнений являются пары чисел , количество которых равно . Исходные данные обычно задают в виде таблиц, состоящих из двух строк или столбцов, в которых и указывают значения величин  и  попарно. Для определенности будем считать, что исходные данные в первых трех столбцах таблица 1, выделенных серым цветом.

Таблица 1

Из рассмотрения системы уравнений следует, что надо вычислить четыре суммы: , , . . Естественно, что для этих сумм сначала надо вычислить значения функций, стоящих под знаками сумм для каждой пары исходных данных, а затем сложить их по столбцам. Оформление этих действий в виде таблицы и дает математическую вычислительную таблицу, которая одновременно будет тестом для разработки компьютерной вычислительной таблицы, а одновременно и компьютерной программы. Аналогично разрабатывают вычислительные таблицы для любого математического преобразования.

После создания математической вычислительной программы, производят вычисление всех элементов ее вручную (с помощью калькулятора) для конкретного числового множества пар чисел . Убедившись в справедливости всех вычислений, разрабатывают соответствующую в компьютерную вычислительную программу, в которой все вычисления будут выполняться автоматически в соответствии с командами, записанными в клетках вычислительной таблицы.

Чтобы создать компьютерную вычислительную программу, надо освоить систему адресации клеток вычислительной компьютерной таблицы и систему команд, выполняемых в каждой клетке ее.

2.2.Адресация клеток компьютерной вычислительной таблицы

Вычисления производятся в таблице, каждой клетке которой ставится в соответствие двухсимвольный адрес, состоящий из латинской буквы и натурального числа, начиная с единицы. Буква соответствует столбцу, а число  -  строке, на пересечении которой со столбцом находится конкретная клетка (Рис. 4).

a             b                c             d

1

2

3

Рис. 4. Адресация клеток вычислительной таблицы

Клетки, расположенные рядом, можно объединять, но тогда для каждой строки будет своя система буквенных обозначений, которая всегда будет начинаться с буквы «а» (рис. 5). В объединенных клетках можно записывать любые текстовые и формульные выражения.

Рис. 5. Возможные схемы объединения клеток

По этой схеме таблицу легко отформатировать применительно к любому наполнению ее, с необходимыми обоснованиями или комментариями.

2.3. Основные формулы, используемые в редакторе Word

Различают формулы пользователя и функции редактора Microsoft Word.