





Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
Тульский государственный университет
Кафедра прикладной математики и информатики
ЧИСЛЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Лабораторная работа №3
“Решение краевой задачи для однородных эллиптических уравнений методом конечных элементов”
Выполнил студент группы
Принял
Приобретение навыков решения краевой задачи для дифференциальных уравнений с частными производными методом конечных элементов.
Общий вид краевой задачи
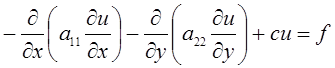 ,
(1)
,
(1)
где x Î[a, b], ![]() ,
, ![]() , с, f – известные функции.
, с, f – известные функции.
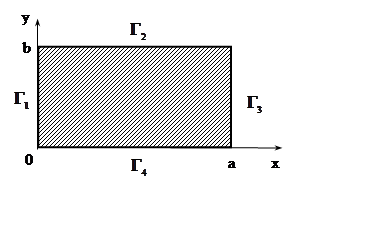 Рассмотрим прямоугольную
область
Рассмотрим прямоугольную
область с заданными граничными условиям
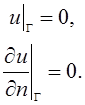 (2)
(2)
Функцию u будем искать в виде
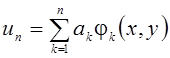 .
.
Задача состоит в минимизации функционала
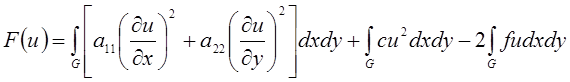
за счет выбора коэффициентов ![]() :
:
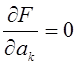 .
.
Введем на данной области некоторую
сетку с шагом ![]() по оси х и шагом
по оси х и шагом ![]() по оси у. Теперь для каждого узла
сетки построим пирамиду единичной высоты, основанием которой являются
шестиугольники вида А.
по оси у. Теперь для каждого узла
сетки построим пирамиду единичной высоты, основанием которой являются
шестиугольники вида А.
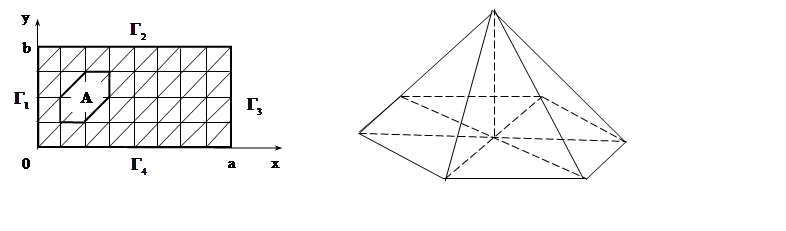 |
Каждая боковая сторона пирамиды ![]() описывается функцией
описывается функцией ![]() , i, j = 1,
2, …, 6, которые строятся в зависимости от ориентации соответствующей грани
относительно осей х и у:
, i, j = 1,
2, …, 6, которые строятся в зависимости от ориентации соответствующей грани
относительно осей х и у:
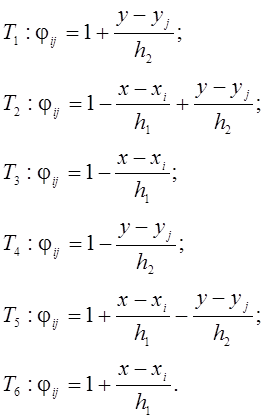 (3)
(3)
Соотношения (3) называются финитными функциями.
Если на границе функция u равна нулю, коэффициенты в узлах сетки сразу полагают равными нулю; если же на границе обращается в нуль производная, то коэффициенты требуется определять.
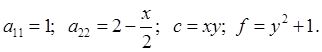
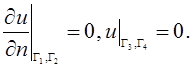
> restart:
> with(plots,display,display3d,setoptions,setoptions3d):
> a1:=1:
a2:=2-x/2:
c:=x*y:
f:=y**2-1:
a:=2:
b:=1:
A:=u->-diff(a1*diff(u,x),x)-diff(a2*diff(u,y),y)+c*u;
![]()
> GetSolvCE_I:=proc(n1,n2) local CE,F,i,j,h1,h2,t,xx,yy,u,v,GetCoeff,st,L; global x,y,phi,f,T;
h1:=a/n1: h2:=b/n2:
for t from 0 to n1 do xx[t]:=t*h1 od:
for t from 0 to n2 do yy[t]:=t*h2 od:
for t from 0 to n2 do u[0,t]:=0;
u[n1,t]:=0 od:
for t from 1 to n1-1 do u[t,0]:=u[t,1];
u[t,n2]:=u[t,n2-1] od:
CE:=(i,j)->simplify(
int(
int(a1*(u[i,j]-u[i+1,j])/h1^2+c*(u[i,j]*(1-(x-xx[i])/h1)
+u[i+1,j]*((x-xx[i])/h1-(y-yy[j])/h2)
+u[i+1,j+1]*(y-yy[j])/h2)*(1-(x-xx[i])/h1),
y = yy[j]..yy[j]+h2*(x-xx[i])/h1),x=xx[i]..xx[i]+h1)+
int(
int(a2*(u[i,j]-u[i,j+1])/h2^2+c*(u[i,j]*(1-(y-yy[j])/h2)+ u[i,j+1]*(-(x-xx[i])/h1 + (y-yy[j])/h2)+ u[i+1,j+1]*(x-xx[i])/h1)*(1-(y-yy[j])/h2),
y = yy[j]+h2*(x-xx[i])/h1..yy[j]+h2), x=xx[i]..xx[i]+h1)+
int(
int(a1*(u[i,j]-u[i-1,j])/h1^2+a2*(u[i,j]-u[i,j+1])/h2^2 + c*(u[i,j]*(1+(x-xx[i])/h1-(y-yy[j])/h2)+u[i,j+1]*(y-yy[j])/h2
-u[i-1,j]*(x-xx[i])/h1)*(1+(x-xx[i])/h1-(y-yy[j])/h2),
y = yy[j]..yy[j] + h2*(x-xx[i]+h1)/h1), x = xx[i]-h1..xx[i])+
int(
int(a1*(u[i,j]-u[i-1,j])/h1^2 + c*(u[i,j]*(1+(x-xx[i])/h1) + u[i-1,j]*((y-yy[j])/h2-(x-xx[i])/h1) - u[i-1,j-1]*(y-yy[j])/h2)*(1+(x-xx[i])/h1),
y = yy[j]+h2*(x-xx[i])/h1..yy[j]), x = xx[i]-h1..xx[i]) +
int(
int(a2*(u[i,j]-u[i,j-1])/h2^2 + c*(u[i,j]*(1+(y-yy[j])/h2) + u[i-1,j-1]*(-(x-xx[i])/h1)+u[i,j-1]*((x-xx[i])/h1 - (y-yy[j])/h2))*(1+(y-yy[j])/h2), y=yy[j]-h2..yy[j]+h2*(x-xx[i])/h1), x=xx[i]-h1..xx[i]) +
int(
int(a1*(u[i,j]-u[i+1,j])/h1^2+a2*(u[i,j]-u[i,j-1])/h2^2+ c*(u[i,j]*(1-(x-xx[i])/h1+(y-yy[j])/h2)-u[i,j-1]*(y-yy[j])/h2+
u[i+1,j]*(x-xx[i])/h1)*(1-(x-xx[i])/h1+(y-yy[j])/h2),
y = yy[j]+h2*(x-xx[i]-h1)/h1..yy[j]), x = xx[i]..xx[i]+h1)):
F:=(i,j)->simplify(
int(
int(f*(1-(x-xx[i])/h1),
y = yy[j]..yy[j]+h2*(x-xx[i])/h1), x = xx[i]..xx[i]+h1) + int(
int(f*(1-(y-yy[j])/h2),
y=yy[j]+h2*(x-xx[i])/h1..yy[j]+h2), x=xx[i]..xx[i]+h1) +
int(
int(f*(1+(x-xx[i])/h1 -(y-yy[j])/h2), y=yy[j]..yy[j]+h2*(x-xx[i]+h1)/h1), x=xx[i]-h1..xx[i])+
int(
int(f*(1+(x-xx[i])/h1),
y = yy[j]+h2*(x-xx[i])/h1..yy[j]), x=xx[i]-h1..xx[i]) +
int(
int(f*(1+(y-yy[j])/h2),
y = yy[j]-h2..yy[j]+h2*(x-xx[i])/h1), x=xx[i]-h1..xx[i]) +
int(
int(f*(1-(x-xx[i])/h1+(y-yy[j])/h2),
y = yy[j]+h2*(x-xx[i]-h1)/h1..yy[j]), x = xx[i]..xx[i]+h1)):
st := time():
L:=simplify({seq(seq(CE(k,m) = F(k,m), m=1..n2-1), k=1..n1-1)}); T:=time()-st:
GetCoeff:=[op(fsolve(L,{seq(seq(u[i,j], j=1..n2-1), i=1..n1-1)}))]:
for t from 1 to (n1-1)*(n2-1) do v[op(1,lhs(GetCoeff[t])),op(2,lhs(GetCoeff[t]))]:=rhs(GetCoeff[t]) od:
for t from 1 to n1-1 do v[t,0]:=v[t,1];
v[t,n2]:=v[t,n2-1] od:
for t from 0 to n2 do v[0,t]:=0;
v[n1,t]:=0 od:
phi:=(x,y,i,j)->`if`((x>xx[i]) and (x<xx[i]+h1) and (y>=yy[j]) and (y<=yy[j]+h2*(x-xx[i])/h1), 1-(x-xx[i])/h1,
`if`((yy[j]+h2*(x-xx[i])/h1<y) and (y<yy[j]+h2) and (xx[i]<=x) and (x<xx[i]+h1),1-(y-yy[j])/h2,
`if`((yy[j]<=y) and (y<yy[j]+h2*(x-xx[i]+h1)/h1) and (x>xx[i]-h1) and (x<xx[i]),1+(x-xx[i])/h1-(y-yy[j])/h2,
`if`((y>=yy[j]+h2*(x-xx[i])/h1) and (y<yy[j]) and (x>xx[i]-h1) and (x<xx[i]),1+(x-xx[i])/h1,
`if`((y>yy[j]-h2) and (y<yy[j]+h2*(x-xx[i])/h1) and (x>xx[i]-h1) and (x<=xx[i]),1+(y-yy[j])/h2,
`if`((y>yy[j]+h2*(x-xx[i]-h1)/h1) and (y<yy[j]) and (x>xx[i]) and (x<xx[i]+h1), 1-(x-xx[i])/h1+(y-yy[j])/h2,0)))))): return(unapply(sum(sum(v[i,j]*phi(x,y,i,j), j=0..n2), i=1..n1-1),x,y)) end:
> N1:=15:N2:=10:P_CE:=GetSolvCE_I(N1,N2):T;
![]()
> plot3d(phi(x,y,2,0),x=0..3*a/N1*1.1, y=0..2*b/N2*1.1,numpoints=35^2);
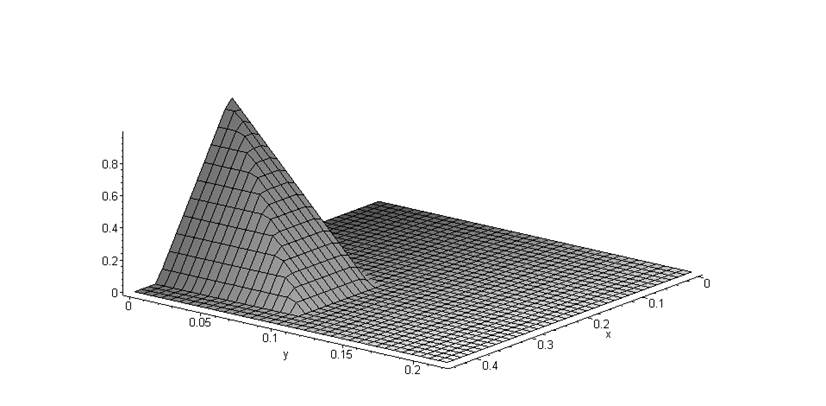
> plot3d(phi(x,y,2,1),x=0..3*a/N1*1.1, y=0..2*b/N2*1.1,numpoints=35^2);
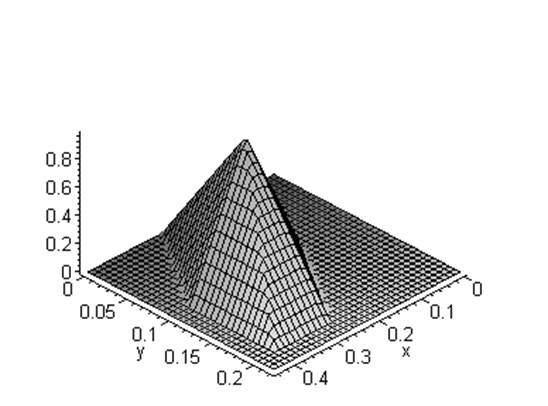
> plot3d(P_CE(x,y),x=0..a,y=0..b);
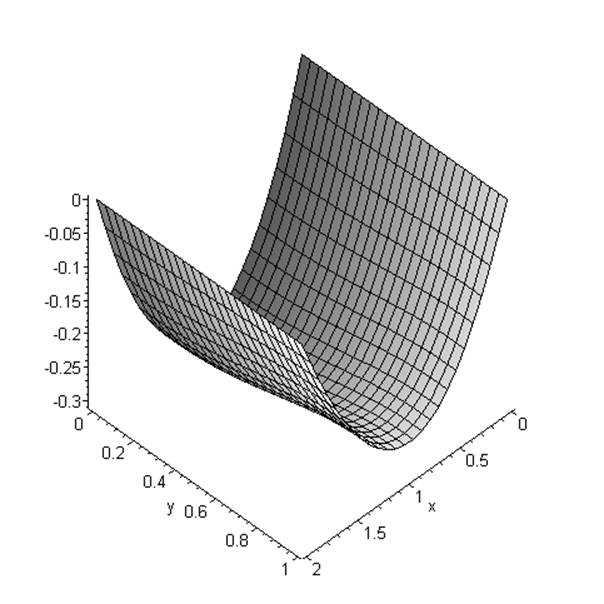
> u:=1-(2*x/a-1)^2;
f:=simplify(A(u));
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.