Нахождение передаточной функции системы, определение ее устойчивость, нахождение частотных характеристик

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

Экономико-Математические Модели.

Контрольно-Курсовая Работа.

13 вариант.

Выполнил студент группы                       

Принял                                                                      

Тула, 2005г.

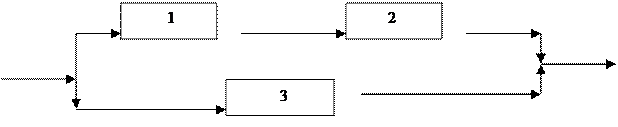
1.  Дана САУ, состоящая из блоков с характеристиками

      

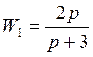
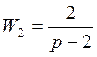
Найти передаточную функцию системы, определить ее устойчивость, найти частотные характеристики

Выполнение:

Воспользуемся математическим пакетом Maple 9:

> restart;

> W1:=2*p/(p+3);

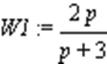
> W2:=2/(p-2);

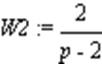
> W3:=2*p-1;

>

> W:=simplify((W1*W2)+W3);

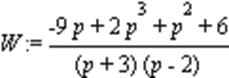
> c:=[solve((p+3)*(p-2)=0)];

Так как есть корни справа от мнимой оси – система неустойчива.

> assume(w,real);

> p:=I*w;

> W;

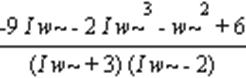
> P:=Re(W);

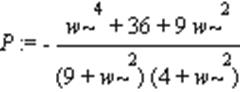
> Q:=Im(W);

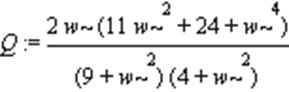
Амплитудно-частотная характеристика:

> A:=simplify(sqrt(Q^2+p^2));

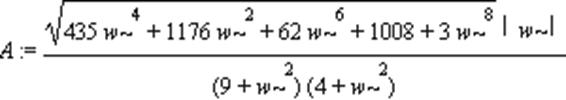
Фазово-частотная характеристика:

> F:=simplify(arctan(Q/P));

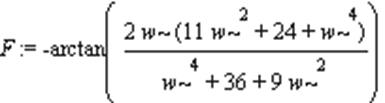
> plot(A, w=-100..100);

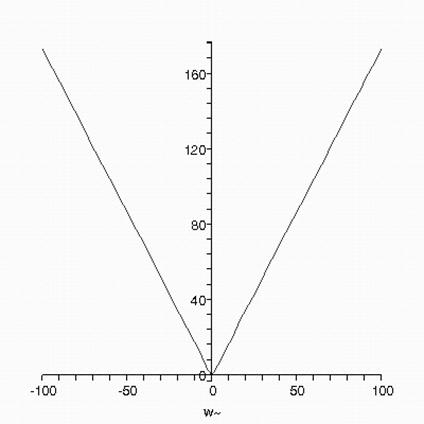
График амплитудно-частотной характеристики.

> plot(F,w);

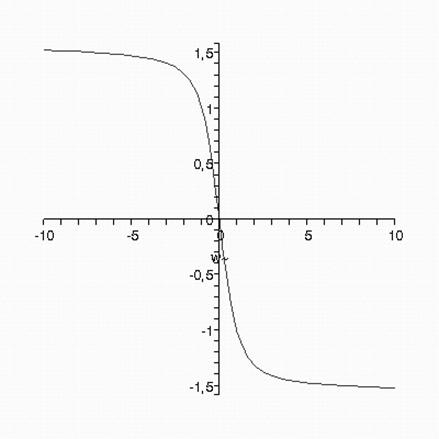
График фазово-частотной характеристики.

2.  Теперь эту систему дополним отрицательной обратной связью с характеристикой

Проделать те же исследования, сравнить результаты.

> p:=l;

> Woc:=1+p;

> W;

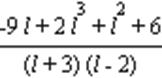
> WW:=simplify(W/(1+W*Woc));

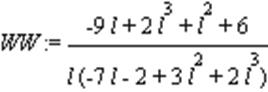
> c:=[evalf(solve(l*(-7*l-2+3*l^2+2*l^3)=0))];

Так как есть корни на мнимой оси – система на грани устойчивости.

> l:=I*w;

> WW;

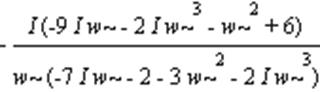
> P1:=simplify(Re(WW));

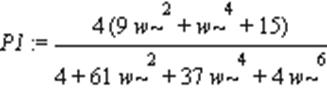
> Q1:=simplify(Im(WW));

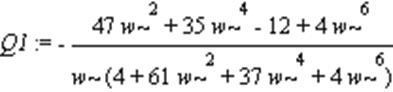
Фазово-частотная характеристика:

> F1:=simplify(Q1/P1);

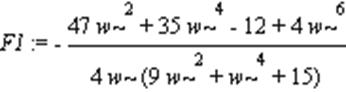
Амплитудно-частотная характеристика:

> A1:=simplify(sqrt(Q1^2+P1^2));

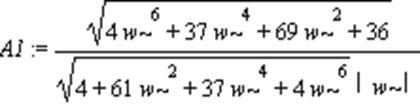
> plot(A1,w);

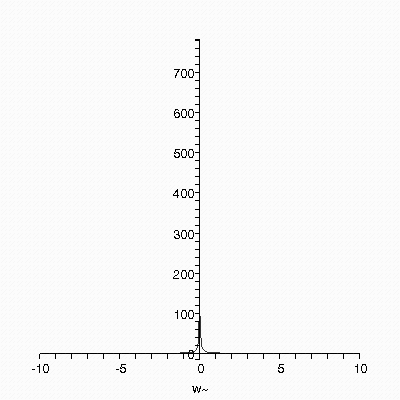
График амплитудно-частотной характеристики.

plot(F1,w);

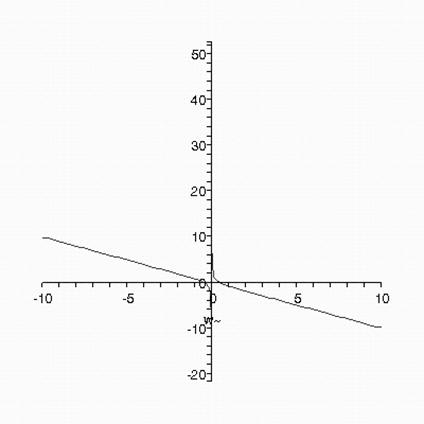
График фазово-частотной характеристики.

При дополнении системы отрицательной обратной связью система стала на грани устойчивости. Изменились частотные характеристики.

3.Передаточная функция системы

 

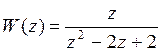
Устойчива ли она?

Решение:

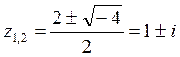
Следовательно, система неустойчива, так как полюса по модулю больше единицы.