24. Вексель учтен за два года до даты его погашения по простой учетной ставке 20%. Какова доходность учетной операции в виде простой процентной ставки?
1) 35%; 2) 25%; 3) 28%; 4) 33%; 5) 30%.
25. Вексель учтен за 10 месяцев до даты его погашения по простой учетной ставке 12%. Какова доходность учетной операции в виде простой процентной ставки?
1) 13%; 2) 15%; 3) 11%; 4) 12%; 5) 14%.
26. Вексель учтен за 500 дней до даты его погашения по учетной ставке 9%. Какова доходность учетной операции в виде простой процентной ставки (количество дней в году принять равным 360)?
1) 13%; 2) 9%; 3) 10%; 4) 11%; 5) 12%.
27.Вкладчик положил в банк 1 тыс. руб. на 3 года под 12% годовых. Какую сумму получит вкладчик по истечении срока вклада при начислении простых процентов?
1) 1630 руб.; 2) 1360 руб.; 3) 1500 руб.; 4) 1300 руб.; 5) 1380 руб.
28. Вкладчик положил в банк 5 тыс. руб. на 3 года под 15% годовых. Ставка налога на проценты составляет 10%. Какую сумму получит вкладчик при начислении простых процентов?
1) 6750 руб.; 2) 6520 руб.; 3) 6620 руб.; 4) 6600 руб.; 5) 6650 руб.
29.Вкладчик положил в банк 1000 $ на два года под 16 % годовых. Какую сумму получит вкладчик при начислении простых процентов?
1) 1300 $; 2) 1395 $; 3) 1350 $; 4) 1320 $; 5) 1316 $.
30. Вкладчик положил в банк 600 $ на 90 дней под 13 % годовых. Ставка налога на проценты составляет 10%. Какую сумму получит вкладчик при начислении простых процентов (количество дней в году принять равным 365)?
1) 630 $ ; 2) 620 $; 3) 617 $; 4) 615 $; 5) 630 $.
31.Вкладчик положил в банк 5 тыс. руб. на 650 дней под 12% годовых. Какую сумму получит вкладчик при начислении простых процентов (количество дней в году принять равным 365)?
1) 6068,5 руб.; 2) 5900,3 руб.; 3) 6150 руб.;
4) 6090,5 руб.; 5) 6005,5 руб.
32.Вкладчик положил в банк 200 тыс. руб. на 19 месяцев под 14% годовых. Ставка налога на проценты составляет 7%. Какую сумму получит вкладчик при начислении простых процентов?
1) 249 тыс. руб.; 2) 241 тыс. руб.; 3) 250 тыс. руб.;
4) 230 тыс. руб.; 5) 239 тыс. руб.
33. Доходность ![]() за период времени Т при годовой
простой процентной ставке
за период времени Т при годовой
простой процентной ставке ![]() равна:
равна:
1) 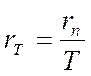 ; 2)
; 2)![]() ; 3)
; 3)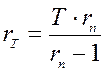 ;
;
4)![]() ; 5)
; 5) ![]() .
.
34. При изменяющейся во времени процентной ставке для простых процентов наращенная к концу срока сумма определится следующим образом:
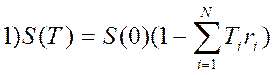 ;
; 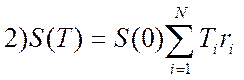 ;
; 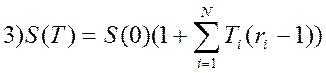 ;
; 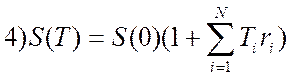 ;
; 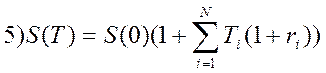 .
.
35. Фирма решила вложить свободные средства в банк. Сколько времени необходимо для увеличения этих средств в 3 раза, если банк использует начисление простых процентов и годовая ставка составляет 10%?
1) 20 лет; 2) 19,7 лет; 3) 21 год ; 4) 20,5 лет.; 5) 18,5 лет.
36. Фирма решила вложить свободные средства в банк. Сколько времени необходимо для увеличения этих средств в 1,5 раза, если банк использует начисление простых процентов и годовая ставка составляет 10 %?
1) 5,5 лет; 2) 5,7 лет; 3) 4,5 года; 4) 5 лет ; 5) 5,2 года.
37. Фирма решила вложить свободные средства в банк. Сколько времени необходимо для увеличения этих средств на 40%, если банк использует простую схему начисления процентов и годовая ставка составляет 12 %?
1) 3,3 года; 2) 3 года; 3) 3,5 года; 4) 3,2 года; 5) 2,9 года.
38. Фирма решила вложить свободные средства в размере 5000 $ в банк. Какая должна быть годовая простая процентная ставка банка, чтобы по истечении 2-х лет фирма получила 7300 $?
1) 20 %; 2) 25 %; 3) 19 %; 4) 22 %; 5) 23%.
39. Фирма решила вложить свободные средства в размере 4000 $ в банк. Какая должна быть годовая простая процентная ставка банка, чтобы по истечении 19 месяцев фирма получила 5250 $?
1) 20 %; 2) 25 %; 3) 19 %; 4) 22 %; 5) 18%.
40. Банк А предлагает разместить вклад на 91 день под простую годовую ставку 14%. Банк Б предлагает разместить вклад на 150 дней под 7% годовых сложных. Каково отношение наращенной суммы в банке А к наращенной сумме банка Б, если в каждый из них можно разместить одинаковую сумму денег (число дней в году принять равным 360)?
1) 1,009; 2) 1,007; 3) 0,997; 4) 1,056; 5) 1,002.
41. Банк А предлагает разместить вклад с 1.12.04 по 1.02.05 (включительно) под простую годовую ставку 12%. Банк Б предлагает разместить вклад с 1.12.04 по 28.02.05 (включительно) под 10% годовых сложных. Каково отношение наращенной суммы в банке А к наращенной сумме банка Б, если в каждый из них можно разместить одинаковую сумму денег (число дней в году принять равным 360)?
1) 1,005; 2) 0,995; 3) 0,757; 4) 0,901; 5) 0,912.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.