Принятие решений с помощью нечетких множеств. Закрепление знаний по теории нечетких множеств, изучение ситуационной нечеткой модели принятия решений

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

теория выбора и принятия решений

Лабораторная работа № 4

ПРИНЯТИЕ РЕШЕНИЙ С ПОМОЩЬЮ НЕЧЕТКИХ МНОЖЕСТВ

Выполнил: ст. гр. 530 211                                                             

Проверил:                                                                                        

Тула 2005

ЦЕЛЬ

Закрепление знаний по теории нечетких множеств, изучение ситуационной нечеткой модели принятия решений.

1. Описание объекта принятия решений

Объект принятия решений - расчётный центр универсального магазина самообслуживания, необходимо принимать решения по числу обслуживающих в данный момент покупателей кассиров. Кассовых аппаратов в магазине имеется 6 штук.        

Набор признаков: 1) время, принимает значения от 9 до 20 часов, нечёткие значения: утро, день, вечер; 2) день недели, принимает значения от 1 до 7, нечёткие значения: рабочий, выходной.

Степени соответствия: 1 - "соответствует", 0 - "не соответствует".

2. Описание лингвистических переменных

<«Время», {«утро», «день», «вечер»}, [9, 20]>

Нечеткие переменные:

<«утро», [10, 30], >, нечеткое множество  ={<1,9>,<0.6,12>,<0.2,14>,<0,17>,<0,20>}

<«день», [10, 30], >,

={<0,9>,<0.6,12>,<1,14>,<0.6,17>,<0,20>}

<«вечер», [10, 30], >,

={<0,9>,<0,12>,<0.3,14>,<0.7,17>,<1,20>};

<«День недели », {«рабочий», «выходной»}, {1, 2, 3, 4, 5,6,7}>

<«рабочий», {1, 2, 3, 4, 5,6,7}, >,

={<1,1>,<1,2>,<1,3>,<1,4>,<1,5>,<0,6>,<0,7>};

<«выходной», {1, 2, 3, 4, 5,6,7}, >,

={<0,1>,<0,2>,<0,3>,<0,4>,<0,5>,<1,6>,<1,7>};

3. Графики функций принадлежности для нечетких значений признаков

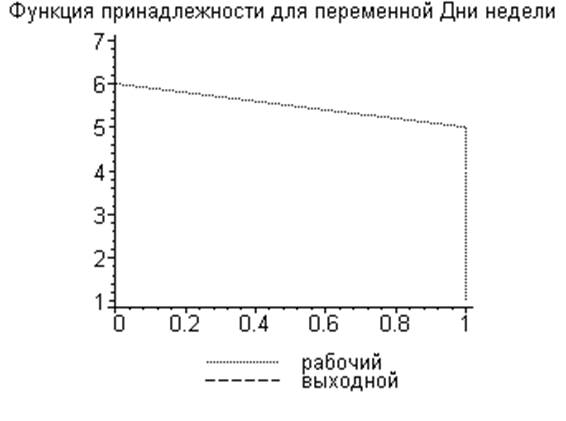
4. Универсальные шкалы и графики функций отображения

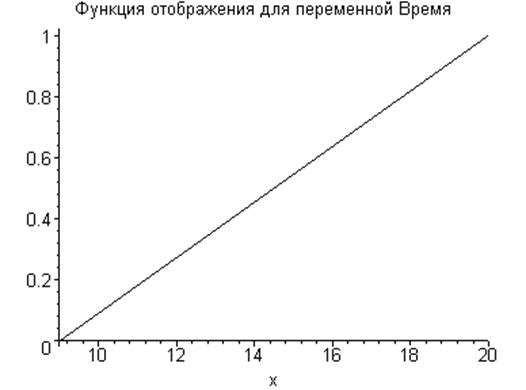
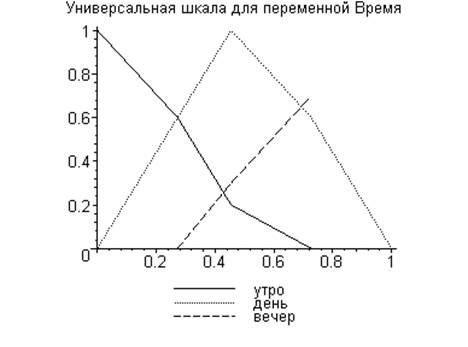
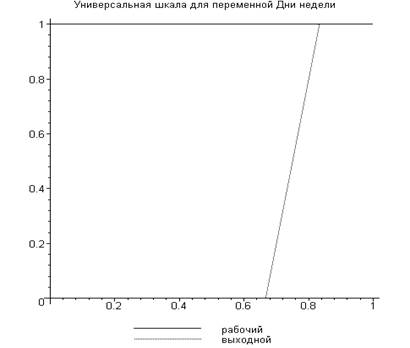
5. Описание эталонных ситуаций

Набор эталонных ситуаций характеризует все возможные состояния объекта управления. В нашем случае имеем  6 эталонных ситуаций.

1 — «соответствует», 0 — не соответствует

S1={<<0/утро>,<0/день>,<1/вечер>/время>,

<0/рабочий>,<1/выходной>/день недели>>}

решение: число аппаратов равно 6;

S2={<<0/утро>,<0/день>,<1/вечер>/время>,

<1/рабочий>,<0/выходной>/день недели>>}

решение: число аппаратов равно 5;

S3={<<0/утро>,<1/день>,<0/вечер>/время>,

<0/рабочий>,<1/выходной>/день недели>>}

решение: число аппаратов равно 5;

S4={<<0/утро>,<1/день>,<0/вечер>/время>,

<1/рабочий>,<0/выходной>/день недели>>}

решение: число аппаратов равно 4;

S5={<<1/утро>,<0/день>,<0/вечер>/время>,

<0/рабочий>,<1/выходной>/день недели>>}

решение: число аппаратов равно 3;

S6={<<1/утро>,<0/день>,<0/вечер>/время>,

<1/рабочий>,<0/выходной>/день недели>>}

решение: число аппаратов равно 4;

Эталонная ситуация	время			День недели		Число кассовых аппаратов
	Н	С	В	Б	Н
S1	0	0	1	0	1	6
S2	0	0	1	1	0	5
S3	0	1	0	0	1	5
S4	0	1	0	1	0	4
S5	1	0	0	0	1	3
S6	1	0	0	1	0	4

Пусть имеем следующую реальную ситуацию ,  подлежащую решению. Необходимо принять решение о числе аппаратов, если время 16 часов и день недели воскресенье.

Для принятия решения сравним возникшую ситуацию с эталонными на степень нечеткого включения:

,

,

,

.

Ситуацию  представим в виде:

S6={<<0/утро>,<1/день>,<0/вечер>/время>,

<0/рабочий>,<1/выходной>/день недели>>}

решение: число аппаратов равно 4;

Пусть  заданный порог . Теперь необходимо найти степень включения между ситуацией  и всеми эталонными ситуациями. Если , то ситуацию  считаем наиболее приближенной к  и принимаем решение, соответствующее ситуации .

Так

[1&(1 – 0 + 0)]&[1&(1 – 1 + 1)]&[1&(1 – 0 + 0)]&[1&(1 – 0 + 1)] & [1&(1-1+1)]=1&1&1&1&1=1

Так как1 , то считаем исходную ситуацию, близкой к ситуации S3. Принимаем решение о необходимости 5 кассовых аппаратов.