Случайные процессы. Элементарная случайная функция Y (t). Среднеквадратическое отклонение случайного процесса, страница 4

извольная функция; +D) |R_x (t₁,t₂)| ≤ [σ_x (t₁) + σ_x (t₂)].

33. Укажитеправильноеопределениевзаимнойспектральной плотности:

;

B)  ;

C)  ;

D);

2

34. Функция комплексной переменной, определяемая какотношениепреобразованныхпоЛапласувыходного сигнала к входному сигналу при нулевых начальных условиях, называется

A)  Амплитудно-частотнойхарктеристикойсистемы;

B)  Взаимной спектральной плотностью; C) Автокорреляционной функцией; +D) Передаточной функцией.

35.  Какая из перечисленных ниже случайных функций X (t) является стационарной, если известны ее математическоеожидание, дисперсияиавтокорреляционная функция?

+A)           m_X (t)       =        5; D_X (t)        =        1;R_X (t₁,t₂)         =

;
B)          mX (t)       =        0; DX (t) ( a при |t2 − t1| ≤ T ; 0 при |t2 − t1| > T	=	a; RX (t1,t2)	=
C)          mX (t)       =        5; DX (t)	=	1; RX (t1,t2)	=

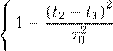при |t₂ − t₁| ≤ τ₀

0 при |t2 − t1| > τ0
D)          mX (t)       =             λt; DX (t)	=	λt; RX (t1,t2)	=

λmin(t₁,t₂);

36.  Нормированная взаимно корреляционная функция определяется как

A) r_xy (t₁,t₂) = M [(x(t₁) − m_x (t₁))(y (t₂) − m_y (t₂))];

                                                                x ( ₁)      ( ₂)

(x(t₁) − m_x (t₁))(y (t₂) − m_y (t₂))

C)  xy 1 2              

σ_x (t )σ (t )

D)  ;

37. Случайнаявеличина соотвествующаязначению случайной функции при фиксированном значении аргумента t = t₀, называется:

A)  реализацией;

B)  траекторией;

C)  сечением;

+D) выборочной функцией;

38. Укажитенеправильнеосвойствовзаимнойкорреляционной функции:

+A) R_xy (−τ) = −R_xy (τ);

B)  (0));

C)  |R_xy (τ)^|2 ≤ R_x (0)R_y (0);

D)  ^RR_(C) R_xy (τ)ϕ(τ)dτ ≥ 0, где ϕ(τ) произвольная функция.

39. Какая величина не является вероятностной характеристикой выбросов случайных процессов?

A) среднеевремянахождениепроцессавышеуровня; B) среднее расстояние между выбросами;

+C) среднеезначениепроцессавнаблюдаемыйпериод;

D) средняя площадь одного выброса.

40. Каковаразмерность: 1) спектральнойплотности; 2) нормированной спектральной плотности?

A)  1) размерностьквадратаслучайногопроцесса, деленная на размерность частоты; 2) безразмерна;

B)  1) размерность квадрата случайного процесса; 2) безразмерна;

C)  1) размерностьквадратаслучайногопроцесса, деленная на квадрат размерности частоты; 2) обратная размерности частоты в квадрате;

+D) 1) размерность квадрата случайного процесса, деленная на размерность частоты; 2) обратная размерности частоты.

41. Укажите неправильное свойство взаимной спектральной плотности:

A) |S_XY (ω)|² ≤ S_X (ω)S_Y (ω);

+B) S_XY (ω) – комплексная величина;

C)  S_XY (ω) > 0;

D)  0;

42.                     Если известна автокорреляционная функция

R_x (t₁,t₂) случайного процесса, то его дисперсию σ_x² (t) можно определить как

A)  R_x (0,t);

B)  R_x (t,0);

C)  R_x (0,0);

+D) R_x (t,t).

43. Случайный процесс, определенный при t ∈ [a,b], называетсяоднороднымпроцессомснезависимыми приращениями, если:

A) для любых t₀,t₁,...t_n, таких, что a ≤ t₀,...t_n ≤ b случайные величины X (t₀),X (t₁) − X (t₀),...X (t_n) − независимы;

для любых t₀,t₁,...t_n, таких, что a ≤ t₀,...t_n ≤ b случайные величины X (t₀),X (t₁) − X (t₀),...X (t_n) − X (t_n−1) независимы, изаконраспределенияслучайной величины X (t)−X (t₀) независитот t₀, аопределяется лишь длиной интервала;

C)  для любых t₀,t₁,...t_n, таких, что a ≤ t₀,...t_n ≤ b случайные величины X (t₀),X (t₁) − X (t₀),...X (t_n) − X (t_n−1) независимы, изаконраспределенияслучайной величины X (t) − X (t₀) является нормальным;

D)  для любых t₀,t₁,...t_n, таких, что a ≤ t₀,...t_n ≤ b случайные величины X (t₀),X (t₁) − X (t₀),...X (t_n) − X (t_n−1) слабо коррелированы;

44. Нормированная автокорреляционная функция определяется так

A) r_x (t₁,t₂) = M [(x(t₁) − m_x (t₁))(x(t₂) − m_x (t₂))];

                                    M         t                 t            t                 t

;

C); σ_x (t₁)σ (t₂)

D);

σ_x (t₁)σ (t₂)