Исследование реальных потоков событий в системах массового обслуживания. Приобретение навыков расчета характеристик случайных потоков заявок в реальной системе массового обслуживания

Министерство высшего и профессионального образования РФ

Тульский государственный университет

Кафедра прикладной математики и информатики

СЛУЧАЙНЫЕ  ПРОЦЕССЫ

Лабораторная работа №4

Выполнил ст. гр.                             

Проверил к.т.н., доц.                                                                               А

Тула 2001

ИССЛЕДОВАНИЕ   РЕАЛЬНЫХ   ПОТОКОВ   СОБЫТИЙ   В   СИСТЕМАХ   МАССОВОГО   ОБСЛУЖИВАНИЯ

I. ЦЕЛЬ  РАБОТЫ.

Приобретение навыков расчета характеристик случайных потоков заявок в реальной системе массового обслуживания.

II. ЗАДАНИЕ.

Исследовать потоки заявок в реальной системе массового обслуживания: парикмахерской.

Необходимо:

1.  Уяснить физическую сущность основных процессов, протекающих в заданной СМО (парикмахерской);

2.  Определить степень приближения входного потока к простейшему, а закона распределения времени обслуживания одной заявки одним каналом к показательному;

3.  Построить граф состояний и составить математическую модель СМО;

4.  Проанализировать полученные результаты.

III. РЕШЕНИЕ.

1.  Весь период времени наблюдения за входным потоком составляет 600 минут (10 часов). Разобьем этот период на 20 интервалов по 30 минут каждый. В каждом интервале определим число клиентов, приходящих в парикмахерскую. В результате получим следующие данные:

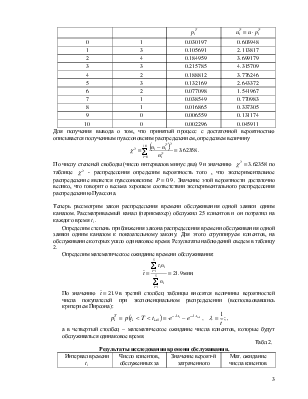
2.  Определим степень приближения входного потока к простейшему. Для этого сгруппируем интервалы, в которых было одинаковое число пришедших клиентов. Результаты наблюдений сведем в таблицу 1.

Определим математическое ожидание числа клиентов в течении принятого интервала :

.

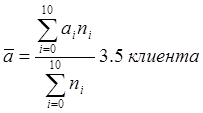По значению в третий столбец таблицы вносятся величины вероятностей числа покупателей при пуассоновском распределении:

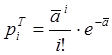, а в четвертый столбец – математическое ожидание числа интервалов, в течении которого пришло одинаковое число клиентов.

Табл.1.

Результаты исследования потока клиентов в парикмахерской.

Для получения вывода о том, что принятый процесс с достаточной вероятностью описывается полученным пуассоновским распределением, определяем величину

.

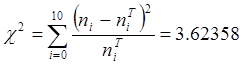По числу степеней свободы (число интервалов минус два) 9 и значению   по таблице  - распределения определим вероятность того , что экспериментальное распределение является пуассоновским: . Значение этой вероятности достаточно велико, что говорит о весьма хорошем соответствии экспериментального распределения распределению Пуассона.

Теперь рассмотрим закон распределения времени обслуживания одной заявки одним каналом. Рассматриваемый канал (парикмахер) обслужил 25 клиентов и он потратил на каждого время .

Определим степень приближения закона распределения времени обслуживания одной заявки одним каналом к показательному закону. Для этого сгруппируем клиентов, на обслуживание которых ушло одинаковое время. Результаты наблюдений сведем в таблицу 2.

Определим математическое ожидание времени обслуживания:

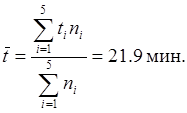
По значению в третий столбец таблицы вносятся величины вероятностей числа покупателей при экспоненциальном распределении (воспользовавшись критерием Пирсона):

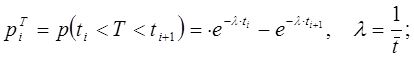, а в четвертый столбец – математическое ожидание числа клиентов, которые будут обслуживаться одинаковое время.

Табл.2.

Результаты исследования времени обслуживания.

Для получения вывода о том, что принятый процесс с достаточной вероятностью описывается полученным экспоненциальным распределением, определяем величину

.

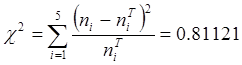По числу степеней свободы (число интервалов минус два) 3 и значению   по таблице  - распределения определим вероятность того, что экспериментальное распределение является пуассоновским: . Значение этой вероятности говорит о достаточно точном соответствии экспериментального распределения показательному распределению.

3.  Построим граф состояний и составим математическую модель СМО.

Основные элементы системы массового обслуживания:

Входной                      Очередь                      Каналы                   Выходной поток                                                                      обслужив-я                     поток

В нашем случае имеем СМО смешанного типа с ограничениями на время ожидания клиента в очереди () и на длину очереди (). Также в данной СМО наблюдаем марковский случайный процесс, т.к. все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими. Число каналов обслуживания – 3. Граф состояний для СМО с ограничением на длину очереди и время ожидания в очереди имеет вид:

                                                                                    …                     

где       - интенсивность потока клиентов (клиента за полчаса);   - производительность каждого канала (); - событие означающее, что клиентов нет;  - работают соответственно 1,2 или 3 парикмахера; - - очередь.