Цифровые методы анализа случайных процессов. Приобретение навыков расчета характеристик случайных процессов по имеющимся данным

Министерство образования и науки РФ

Тульский государственный университет

Кафедра прикладной математики и информатики

СЛУЧАЙНЫЕ ПРОЦЕССЫ

Лабораторная работа № 6

ЦИФРОВЫЕ МЕТОДЫ АНАЛИЗА СЛУЧАЙНЫХ ПРОЦЕССОВ

Выполнил: ст. гр.                                                             

Проверил: доц., к. т. н.                                                         

Тула 2004

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков расчета характеристик случайных процессов по имеющимся данным.

II. ЗАДАНИЕ НА РАБОТУ

По имеющейся реализации (данным) временного ряда вычислить основные характеристики случайного процесса:

-  закон распределения значений процесса;

-  математическое ожидание, среднее квадратическое отклонение и дисперсию значений процесса;

-  автокорреляционную функцию процесса;

-  спектральную плотность процесса.

Ш. ВАРИАНТ ЗАДАНИЯ

Количество сделок (договоров) фирмы по месяцам (ед.): 18, 22, 23, 24, 25, 24, 27, 25, 23, 22, 23, 27, 26, 24, 22, 20, 21, 22, 23, 22, 21, 20, 19, 16, 17, 20, 22, 22, 23, 27, 30, 28, 27, 25, 27, 25, 22, 20, 20, 21, 23, 27, 29, 33, 30, 29, 26, 24, 23, 21, 18, 20, 22, 23, 24, 26.

IV. РЕШЕНИЕ

1). Вычислим мат. ожидание,  среднее квадратическое отклонение и дисперсию значений процесса по формулам:

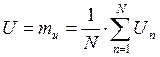
Для упрощения последующих расчетов и выкладок можно преобразовать процесс таким образом, чтобы среднее его значение было равно нулю: x(t) = U(t) - U. Тогда последовательность {x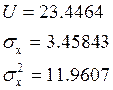_n} значений функции x(t) определяется в виде:

x_n = x(t₀ + Dh) = U_n - U, где  n = 1.. N;                              (6.3)

Несмещенные оценки значений стандартного отклонения s_x и дисперсии s_x² выражаются следующим образом:

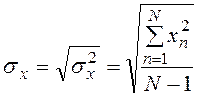
Т. о. получим:

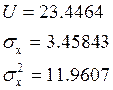
2). Вычислим плотность распределения.

Рассмотрим N значений {x_n}, n = 1,2,3,...,N, преобразованной реализации x(t) стационарного случайного процесса с нулевым средним значением .

{x_n}={-5.44643,-1.44643,-.446429,0.553571,1.55357,0.553571,3.55357,1.55357,

-0.446429,-1.44643,-0.446429,3.55357,2.55357,0.553571,-1.44643,-3.44643,

-2.44643,-1.44643,-0.446429,-1.44643,-2.44643,-3.44643,-4.44643,-7.44643,

-6.44643,-3.44643,-1.44643,-1.44643,-0.446429,3.55357, 6.55357,4.55357, 3.55357,1.55357,3.55357,1.55357,-1.44643,-3.44643,-3.44643,-2.44643,

-0.446429,3.55357,5.55357,9.55357,6.55357,5.55357,2.55357,0.553571,

-0.446429,-2.44643,-5.44643,-3.44643,-1.44643,-0.446429,0.553571,2.55357}

Пусть К - число разрядов, которые охватывают весь диапазон [ x_min, x_max ] изменения функции (процесса). Ширина каждого разряда , а верхняя граница j-го разряда a_j = x_min + j×W, j = 0,1,2,...K.

Определим теперь последовательность из К+2 чисел { b_l }, l = 0, 1, 2,..., К+1, из условий:

b₀ - число значений x, удовлетворяющих неравенству x £ a₀ = x_min;

b₁ - число значений x, удовлетворяющих неравенству a₀ < x £ a₁;

b_j - число значений x, удовлетворяющих неравенству a_j-1 < x £ a_j;

b_k+1 - число значений x, удовлетворяющих неравенству a_k < x £ a_k+1; (a_k+1 = ¥).

В результате N значений последовательности {x_n} будут отсортированы таким образом, что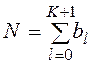

Тогда плотность распределения функции x(t) можно оценить в виде:

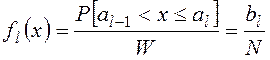
Возьмём K=8 и следуя вышеописанному алгоритму получим:

{b_l}={1,3,7,13,13,7,7,4,0,1}

{f_l}={0.0178571,0.0535714,0.125,0.232143,0.232143,0.125,0.125,0.0714286,0, 0.0178571}

3). Оценка автокорреляционной функции.

Непосредственная оценка

,

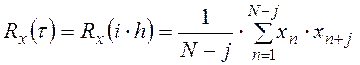где j - номер шага;    m - максимальное число шагов;

R_x(t) - оценка истинного значения АКФ при номере шага j, соответствующем сдвигу  t  = j×h.

При больших N и малых сравнительно с N значениях m можно АКФ вычислить в виде:

,

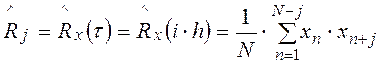где делитель N остается постоянным для всех j, а не принимает переменные значения N- j .

Положим m=4 и проведём вычисления:

j=0; R= 11.9607

j=1; R= 9.55597

j=2; R= 6.02708

j=3; R= 2.2982

j=4; R=-0.708714

4). Определение спектральной плотности.

Первичная оценка спектральной плотности для произвольных значений f диапазона 0 £ f £ f_c может быть определена следующим образом:

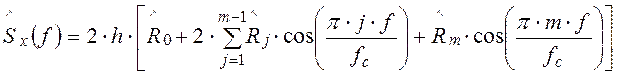,    (6.21)

где f_c = 1/(2×h) частота среза.

Рекомендуется рассчитывать значения функции S_x(f) только для m+1 дискретных частот 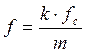, k = 0, …,m(6.22)

В результате будет получено m/2 независимых оценок спектральной плоскости, поскольку оценки, отстоящие друг от друга менее чем на 2×f_c/m, будут коррелированны. На этих дискретных частотах

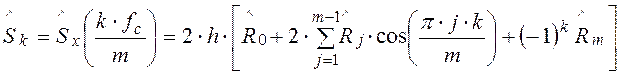     (6.23)

Сглаженная оценка спектральной плотности находится в виде:

S₀ = 0.5×S₀ + 0.5×S₁;