Физика \ Случайные процессы

Цифровые методы анализа случайных процессов. Приобретение навыков расчета характеристик случайных процессов по имеющимся данным, страница 2

Sk = 0.25×Sk-1 + 0.5×Sk + 0.25×Sk+1; k = 1,…,m-1;                                  (6.24)

Sm = 0.5×Sm-1 + 0.5×Sm.

Это сглаживание весовой функции Ханна (иногда называют окном Хэннинга). Аналогичное сглаживание достигается с использованием корреляционной весовой функции Ханна:

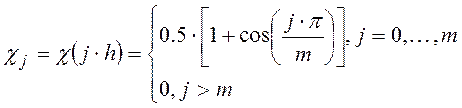                                 (6.25)

при вычислении сглаженных оценок спектральной плотности по формуле:

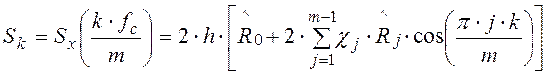                   (6.26) где 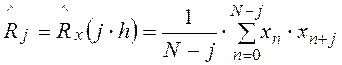, j = 0, …, m.

Если исследуются частотные характеристики и соответствующие функции когерентности системы, может оказаться полезным сглаживание АКФ в формуле (6.26) весовой функцией Парзена:

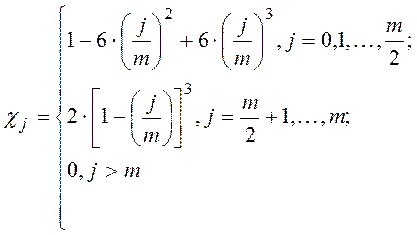                               (6.28)

Использование функции Парзена позволяет получить выборочные оценки функции когерентности, лежащие в интервале [0,1], что не всегда бывает при использовании функции Ханна, которая дает оценки функции когерентности, лежащие в более широком интервале, зависящем от вида энергетического спектра.

Рекомендации по выбору параметров:

1.  Интервал дискретности h = Dt выбирается таким образом, что

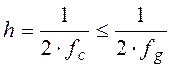,                                                                       (6.29)

где fg £ fc - наиболее высокая частота, присутствие которой возможно в анализируемом процессе. Если задача состоит только в оценке АКФ, то можно положить fс = 2×fg  (в этом случае h = 1/ (4×fg) ). Если же конечной целью является оценка спектральной плотности, то можно принять h = 1/ (2×fg) .

2. Максимальное число шагов m для АКФ выбирается таким образом, что

m = 1/(BS×h)

где BS - желаемая  эквивалентная разрешающая  способность при расчете энергетического спектра;

 3. Объем выборки N выбирается таким, что   N = m/e2,                           (6.31)

где e - нормированная стандартная ошибка, задаваемая при расчете спектра.

T = N×h - соответствующая минимальная длина реализации           (6.32).

4. Число степеней свободы при расчете оценок спектра есть

l = 2×BS×T = 2×N/m

Нормированная стандартная ошибка определяется выражением

e = 1/ (BS×T) = m/N                   

Проводя вычисления по вышеописанным формулам получим следующий результат:

S0= 69.948

S1= 57.5064

S2=29.1537,

S3=16.7812,

S4=-3.37456

Листингпрограммы

#include "stdafx.h"

#include "iostream.h"

#include "math.h"

#define N 56

#define K 8

#define m 4

int _tmain(int argc, _TCHAR* argv[])

{

int a[N]={18, 22, 23, 24, 25, 24, 27, 25, 23, 22, 23, 27, 26, 24, 22, 20, 21, 22, 23, 22, 21, 20, 19, 16, 17, 20, 22, 22, 23, 27, 30, 28, 27, 25, 27, 25, 22, 20, 20, 21, 23, 27, 29, 33, 30, 29, 26, 24, 23, 21, 18, 20, 22, 23, 24, 26};

double m_u=0;

for(int i =0; i < N; i++)

m_u+=a[i];

m_u/=double(N);

cout<<"m_u = "<<m_u<<endl;

double x_n[N];

for(i=0;i<N;i++)

x_n[i]=a[i]-m_u;

double sigma_x=0;

for(i = 0; i < N; i++ )

sigma_x+=x_n[i]*x_n[i];

sigma_x=sqrt(sigma_x/(N-1));

cout<<"sigma_x^2="<<sigma_x*sigma_x<<" sigma_x="<<sigma_x<<endl;

double x_min=x_n[0],x_max=x_n[0];

for(i = 0; i < N; i++)

{

cout<<x_n[i]<<",";

if(x_n[i]<x_min) x_min = x_n[i];

if(x_n[i]>x_max) x_max = x_n[i];

}

double W = (x_max-x_min)/K;

cout<<endl<<"x_min="<<x_min<<" x_max="<<x_max<<" W="<<W<<endl;

int b[K+2];

for(i=0;i<K+2;i++)

b[i]=0;

for(i=0;i<N;i++)

if(x_n[i]<=x_min) b[0]++;

for(int j=1;j<K;j++)

{

for(i=0;i<N;i++)

if(x_n[i]<=x_min+j*W&&x_n[i]>x_min+(j-1)*W) b[j]++;

}

for(i=0;i<N;i++)

if(x_n[i]>=x_min+K*W) b[K+1]++;

for(j=0;j<K+2;j++)

cout<<b[j]<<",";

double f_l[K+2];

cout<<endl;

for(i=0;i<K+2;i++)

{

f_l[i]=b[i]/double(N);

cout<<f_l[i]<<",";

}

//оценка автокорреляционной функции.

cout<<endl;

double R[m+1],R_=0;

for(j = 0;j<=m;j++)

{

for(int n = 0; n<=N-j; n++)

R_+=x_n[n]*x_n[n+j];

R[j]=R_/(N-j);

cout<<R[j]<<",";

R_=0;

}

//спектральная плотность

int k;

double S[m+1],h=1.,pr=0,m_one=1;//, f_c=1/h/2., f=k*f_c/m

for(k=0;k<m+1;k++)

{

for(j=1;j<m;j++)

pr+=R[j]*cos(3.141592653*j*k/m);

S[k]=2*h*(R[0]+2*pr+R[m]*m_one);

pr = 0;

m_one*=-1;

}//for

S[0]=0.5*S[0]+0.5*S[1];

for(k=1;k<=m-1;k++)

S[k]=0.5*S[k-1]+0.25*S[k+1]+0.5*S[k];

S[m]=0.5*S[m-1]*0.5*S[m];

cout<<endl;

for(k=0;k<m+1;k++)

cout<<S[k]<<",";

return 0;

}

Скачать файл