







Мат. анализ и ТФКП
1. Модуль интеграла от функции комплексной переменной не превосходит
1) длины кривой интегрирования
2) максимума модуля подынтегральной функции на кривой интегрирования
3) отношения максимума модуля подынтегральной функции на кривой интегрирования к длине кривой
4) произведениямаксимумамодуляподынтегральной функции на кривой интегрирования на длину кривой
2. Интеграл по сумме кривых равен
1) максимуму из интегралов по каждой из кривых
2) минимуму из интегралов по каждой из кривых
3) произведению интегралов по каждой из кривых
4) сумме интегралов по каждой из кривых
3. Интеграл по замкнутому контуру равен нулю, если
1) в некоторой окрестности контура интегрирования подынтегральная функция аналитична
2) контур является границей области, в некоторой окрестностикоторойподынтегральнаяфункцияаналитична
3) контур является границей области, и в некоторой окрестности контура интегрирования подынтегральная функция аналитична
4) контур является границей односвязной области
4. Интеграл по замкнутому контуру равен нулю, если 1) контур является границей односвязной области
2) подынтегральная функция является аналитической в некоторой окрестности контура интегрирования 3) подынтегральная функция является аналитической в односвязной области, содержащей контур интегрирования
4) подынтегральная функция является аналитическойводносвязнойобласти, содержащейсявнутриконтура интегрирования
5. Интегралкакфункцияверхнегопределаотфункции, аналитической в односвязной области, называется
1) вариацией
2) мажорантой
3) первообразной
4) производной
6. Степенной ряд совпадает с рядом 1) Тейлора своей суммы
2) Тейлора целой функции
3) Фурье своей суммы
4) Фурье целой функции
7. Функция комплексной переменной называется аналитической в точке, если она
1) аналитична в некоторой окрестности этой точки 2) дифференцируема в этой точке
3) непрерывна в некоторой окрестности этой точки
4) непрерывна в этой точке
8. Функция, аналитическая в точке, представляется в виде
1) бесконечного произведения Вейерштрасса
2) дробно-линейной функции
3) отношения двух целых функций
4) суммы ряда Тейлора
9. Наименьшийиндекс, прикоторомкоэффициентряда
Тейлора отличен от нуля, называется
1) вычетом
2) порядком нуля
3) порядком полюса
4) пределом функции
10. Нули аналитической функции являются
1) изолированными
2) неограниченными в совокупности
3) ограниченными в совокупности 4) простыми
11. Остаточный член в форме Пеано в формуле Тейлора f (x) = P5 (x,a)+R5 (x,a), где P5 (x,a) — многочлен
Тейлора пятой степени, имеет вид
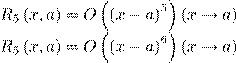 1)
1)
2)
3)![]()
4)![]()
12. Остаточный член в форме Лагранжа в формуле
Тейлора f (x) = P5 (x,a)+R5 (x,a), где P5 (x,a) — многочлен Тейлора пятой степени, имеет вид
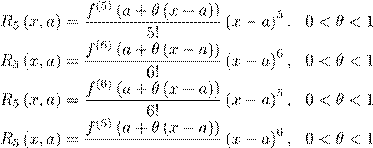 1)
1)
2)
3)
4) 5!
13. Многочлен Тейлора — Маклорена пятой степени для функции f (x) = ex имеет вид
1) 1
2)  1 +
1 +
3) 1 +
4) 1 +
2 3 4 5
14. Многочлен Тейлора — Маклорена пятой степени для функции f (x) = sinx имеет вид
 1)
1)
2)
3)
4)
15.
![]() Маклорена пятой степени для функции f (x)
= cosx имеет вид
Маклорена пятой степени для функции f (x)
= cosx имеет вид
1) 1 2) 1
 3) 1 + 4) 1 +
3) 1 + 4) 1 +
16. Многочлен Тейлора — Маклорена пятой степени для функции f (x) = ln(1 + x) имеет вид
 1)
1)
2)
3)
4)
3 4 5 6
17.
Многочлен Тейлора√ —
Маклорена третьей степени для функции f
(x) = 1 +![]() x имеет вид
x имеет вид
1) 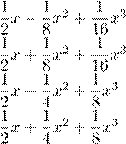 1 +
1 +
2) 1 +
3) 1 +
4) 1 +
18. Формула Тейлора — Маклорена (четвертой степени) с остаточным членом в форме Пеано для функции f (x) = sinx имеет вид
1) 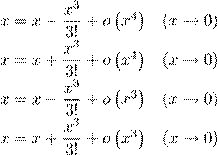 sin
sin
2) sin
3) sin
4) sin
19. Формула Тейлора — Маклорена (третьей степени) с остаточным членом в форме Пеано для функции f (x) = cosx имеет вид
1) 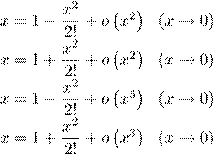 cos
cos
2) cos
3) cos
4) cos
20. Формула Тейлора — Маклорена (третьей степени) с остаточным членом в форме Пеано для функции f (x) = e−x имеет вид
1)
2)
3)
4)
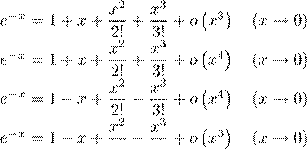 2! 3!
2! 3!
21. Мелкость разбиения T =
{a = x0 < x1 < ··· < xn = b} отрезка [a,b] — это
1) max (xi−1 − xi)
16i6n
2) min (xi − xi−1)
16i6n
3) max (xi − xi−1)
16i6n
4) min (xi−1 − xi)
16i6n
22. Верхние суммы Дарбу для функции f(x) и разбиения T = {a = x0 < x1 < ··· < xn = b} отрезка [a,b] — это
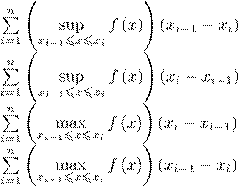 1)
1)
2)
3)
4)
23. Нижние суммы Дарбу для функции f (x) и разбиения T = {a = x0 < x1 < ··· < xn = b} отрезка [a,b] — это
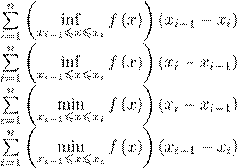 1)
1)
2)
3)
4)
24. Приизмельченииразбиенияотрезкаверхниесуммы
Дарбу
1) могут как увеличиваться, так и уменьшаться
2) не изменяются
3) не увеличиваются
4) не уменьшаются
25. Приизмельченииразбиенияотрезканижниесуммы
Дарбу
1) могут как увеличиваться, так и уменьшаться
2) не изменяются
3) не увеличиваются
4) не уменьшаются
26. Интеграл Римана от функции — это
1) верхний предел интегральных сумм, отвечающих размеченным разбиениям, не зависящий от разметки
2) нижний предел интегральных сумм, отвечающих размеченным разбиениям, не зависящий от разметки
3) предел интегральных сумм, отвечающих размеченным разбиениям с фиксированными разметками
4) предел интегральных сумм, отвечающих размеченным разбиениям, не зависящий от разметки
27. Интервал Римана от функции — это
1) верхний предел нижних сумм Дарбу
2) точная нижняя грань верхних сумм Дарбу
3) точная верхняя грань верхних сумм Дарбу
4) точная нижняя грань нижних сумм Дарбу
28. Интеграл Римана от функции — это
1) верхний предел нижних сумм Дарбу
2) нижний предел верхних сумм Дарбу
3) точная верхняя грань верхних сумм Дарбу
4) точная верхняя грань нижних сумм Дарбу 29. Если ограниченная функция интегрируема по Риману на отрезке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.