























































ЛЕКЦИИ
ПО
МАТЕМАТИЧЕСКИМ
МОДЕЛЯМ
В
ЕСТЕСТВОЗНАНИИ
СОДЕРЖАНИЕ
1. Криволинейные системы координат. . . . . . . . . . . . . . . . . . . . . 4
2. Математическое моделирование движения сплошной среды. . . . . . . . 6
2.1. Заданиедвижениясплошныхсред. ПеременныеЛагранжаиЭй-
лера. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.2. О скалярных и векторных полях. . . . . . . . . . . . . . . . . . . 9
2.3. Индивидуальная, локальная и конвективная производная. . . . . 9
2.4. О тензоре деформаций и тензоре скоростей деформаций. . . . . . 10
2.5. Уравнение неразрывности. . . . . . . . . . . . . . . . . . . . . . . 10
2.6. Массовые и поверхностные силы. . . . . . . . . . . . . . . . . . . 11
2.7. Тензор напряжений. . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.8. Уравнение движения сплошной среды. . . . . . . . . . . . . . . . 12
3. Модели гидродинамики идеальной жидкости. . . . . . . . . . . . . . . . 13
3.1. Понятие идеальной жидкости. . . . . . . . . . . . . . . . . . . . . 13
3.2. Уравнение движения идеальной жидкости. . . . . . . . . . . . . . 13
3.3. Уравнение Громеки-Ламбе. . . . . . . . . . . . . . . . . . . . . . . 14
4. Интегралы уравнений движения. . . . . . . . . . . . . . . . . . . . . . . 15
4.1. Интеграл Бернулли. . . . . . . . . . . . . . . . . . . . . . . . . . . 15
4.2. Интеграл Лагранжа-Коши. . . . . . . . . . . . . . . . . . . . . . . 16
4.3. Интеграл Бернулли-Эйлера. . . . . . . . . . . . . . . . . . . . . . 17
5. Математическая модель потенциального движения идеальной несжи-
маемой жидкости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
5.1. Уравнение потенциального движения идеальной несжимаемой
жидкости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
5.2. Функция тока. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
5.3. Комплексный потенциал. . . . . . . . . . . . . . . . . . . . . . . . 19
5.4. Комплексная скорость. . . . . . . . . . . . . . . . . . . . . . . . . 19
5.5. Обтекание цилиндра поступательным потоком. . . . . . . . . . . 20
5.6. Стационарное обтекание сферы потоком идеальной несжимае-
мой жидкости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
6. Модели гидродинамики вязкой жидкости. . . . . . . . . . . . . . . . . . 26
6.1. Уравнение движения вязкой жидкости. . . . . . . . . . . . . . . . 26 6.2. Начальные и граничные условия.
Об изучении движения вязкой жидкости. . . . . . . . . . . . . . . 27
6.3. Уравнение движения в безразмерных величинах. Числа подобия. 28
6.4. Ламинарные и турбулентные течения. . . . . . . . . . . . . . . . 30
6.5. Течение Куэтта. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
6.6. Течение Пуазеля в цилиндрической трубе. . . . . . . . . . . . . . 31
7. Элементы теории пограничного слоя. . . . . . . . . . . . . . . . . . . . . 33
7.1. Понятие пограничного слоя. . . . . . . . . . . . . . . . . . . . . . 33
7.2. Уравнения движения вязкой жидкости в пограничном слое. . . . 33
7.3. Постановка задачи о течении в пограничном слое. . . . . . . . . 35
8. Модели теории упругости . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
8.1. Обобщенный закон Гука . . . . . . . . . . . . . . . . . . . . . . . 36
8.2. Уравнения теории упругости . . . . . . . . . . . . . . . . . . . . . 38
8.3. Уравнение Ламе . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
8.4. Граничные и начальные условия. . . . . . . . . . . . . . . . . . . 39
9. Математическая модель статики упругого тела. . . . . . . . . . . . . . . 40
9.1. Задача статики упругого тела в смещениях. . . . . . . . . . . . . 41
9.2. Задача статики упругого тела в напряжении. . . . . . . . . . . . 41
10. Плоские задачи упругого равновесия. . . . . . . . . . . . . . . . . . . . . 43
10.1. Решение задачи упругого равновесия тонкой пластины. . . . . . 44
11. Математические модели волновых процессов. . . . . . . . . . . . . . . . 44
11.1. Математическая модель распространения звука. . . . . . . . . . 44
11.2. Решение задач рассеивания звука на сфере. . . . . . . . . . . . . 46
11.3. Математическая модель распространения звуковых волн в вяз-
кой жидкости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
11.4. Математическая модель распространения упругих волн. . . . . . 51
11.5. Математическаямодельраспространенияэлектромагнитныхволн. 53
1. Криволинейные системы координат.
При проведении математического моделирования и последующего математического решения задач важное значение имеет правильный выбор системы координат. От удачного выбора системы координат зависит возможность разделения переменных в дифференциальных уравнениях, простота приемов удовлетворения граничных условий и т.п.
Положение математической точки в пространстве трех измерений можно определять как заданием трех ее декартовых координат (x,y,z) или радиус-вектора r¯ с проекциями x,y,z, так и любой другой тройкой чисел q1,q2,q3 — криволинейных координат, связанныхвзаимно-однозначнымфункциональнымсоответствиемскоординатами (x,y,z):
x = x(q1,q2,q3),
y = y(q1,q2,q3), (1) z = z(q1,q2,q3)
или эквивалентным векторным соотношением:
r¯ = ¯r(q1,q2,q3).
Изменяя только одну из криволинейных координат и сохраняя постоянными остальные две, получим в трехмерном пространстве некоторую кривую, называемую координатной линией. Координатную линию будем обозначать:
(qi) i = 1,2,3.
Через точку M проведем три координатные линии (q1),(q2),(q3). Если в точке M проведем касательные к координатным линиям в сторону возрастания отдельных координат, тополучимкоординатныеоси. Орты (единичныевекторы) координатных осей будут равны:
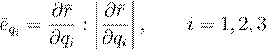 .
.
Если в каждой точке M пространства, координатные оси попарно ортогональны, то имеем ортогональную криволинейную систему координат. На практике ортогональные координаты применяются наиболее часто. Введем в рассмотрение так называемые коэффициенты Ламе — Hqi.
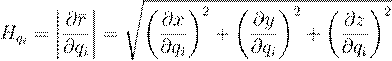 .
.
Дифференциал дуги координатной линии:
![]() .
.
В ортогональной системе координат дифференциал dS произвольно ориентированнойдуги, складываетсяиздифференциаловдугкоординатныхлинийпоправилу:
![]() .
.
Введем в рассмотрение координатные поверхности и касательные к ним координатные плоскости. Координатные поверхности будем обозначать [qi]. Уравнение координатной поверхности [qi] получим из (1), если будем считать постоянной координату qi и переменными остальные две координаты.
В случае ортогональной системы координат через каждую точку пространства M можно провести три координатные поверхности и три взаимно перпендикулярные координатные плоскости. Каждая координатная ось будет перпендикулярной к соответствующей ей координатной поверхности. Попарным перемножением дифференциаловдугкоординатныхлинийполучимэлементарныекоординатныеплощадки:
dσ1 = dSq2 · dSq3 = Hq2Hq3dq2dq3; dσ2 = dSq1 · dSq3 = Hq1Hq3dq1dq3; dσ3 = dSq1 · dSq2 = Hq1Hq2dq1dq2.
Выражение для элемента объема имеет вид:
dτ = dSq1dSq2dSq3 = Hq1Hq2Hq3 · dq1dq2dq3.
Запишем основные операции теории поля в криволинейных координатах
grad![]() ;
;
div ¯![]() ;
;
rot¯![]()
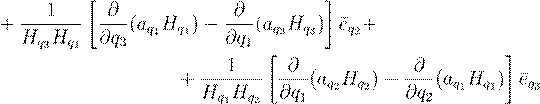 ;
;
∆u = divgradu.
Заметим, что
∆¯u = graddiv ¯u − rotrot ¯u.
При решении задач следует выбирать такую систему координат, в которой одна из координатных поверхностей совпадает с формой рассматриваемого тела или с формой рассматриваемой области.
В качестве примера рассмотрим цилиндрическую и сферическую системы координат.
Цилиндрическая система координат — ρ,ϕ,z:
0 ≤ ρ < ∞,
0 ≤ ϕ ≤ 2π,
−∞ < z < ∞.
Связь цилиндрической системы координат с декартовыми.
x = ρcosϕ,
y = ρsinϕ, z = z.
Определим коэффициенты Ламэ:
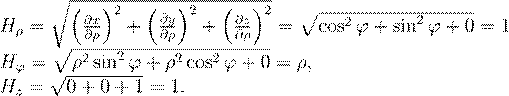 ,
,
[ρ] — цилиндрическая поверхность; [ϕ] — полуплоскость; [z] — плоскость.
Сферическая система координат — r,θ,ϕ:
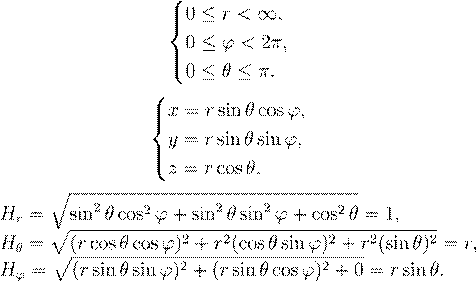
[r] — сфера;
[θ] — конус;
[ϕ] — полуплоскость.
2. Математическоемоделированиедвижениясплошной среды.
Механика сплошной среды изучает движение газообразных, жидких и твердых деформированныхтел. Есливтеоретическоймеханикеизучаетсядвижениематериальнойточки, дискретнойсистемыматематическихточекиабсолютнотвердоготела, то вмеханикесплошнойсредырассматриваетсядвижениетакихматериальныхтел, которыезаполняютпространствонепрерывно, сплошнымобразом, ирасстояниемежду точкамикоторыхвовремядвиженияменяется. Теоретическоерешениетехилииных проблеммеханикисплошнойсреды имееточеньбольшое практическое значение, так как позволяет целесообразно проектировать механические конструкции (самолеты, балочные конструкции и др.) и заранее планировать эксплуатационные характеристики объектов.
В настоящее время условно механику сплошной среды можно разделить на две крупные области:
– механика жидкостей и газов (гидродинамика); – механика твердых деформируемых сред.
Гидродинамика включает следующие основные разделы:
механика идеальной жидкости; механика вязкой жидкости; механика турбулентных течений; аэродинамика; механика фильтрационных течений.
Механика деформируемых твердых тел имеет следующие основные разделы:
теория упругости; теория пластичности; механика сыпучих тел;
В механике сплошной среды рассматриваются математические методы изучения материальных объектов, устанавливаются общие свойства и законы движения тел. Как правило, даже в простейших случаях математически сформулированные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.