Решение плоской задачи теории упругости. Решение задачи о напряженном состоянии в плоской пластине с применением ЭВМ

Министерство образования Российской Федерации

Тульский государственный университет

Кафедра прикладной математики и информатики

Математические модели в естествознании

Лабораторная работа №5

Выполнил: ст. гр.                                              

Принял:                                                                  

Тула 2002

Решение плоской задачи теории упругости

I.  Цель работы.

Решение плоской задачи теории упругости о напряженном состоянии в плоской пластине методом конечных разностей с применением ЭВМ.

II.  Решение задачи о напряженном состоянии в плоской пластине с применением ЭВМ.

В случае двумерных задач теории упругости, при отсутствии объемных сил и при заданных усилиях на границе, напряжения определяются функцией напряжения , которая удовлетворяет бигармоническому уравнению

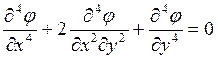                                                   (1)

и граничным условиям

,                                           (2)

где     – направляющие косинусы нормали к границе;

 – компоненты поверхностных сил, отнесенных к единице площади в данной точке границы;

 – нормальные напряжения;

 – касательное напряжение.

Величины ,  выражаются через функцию напряжения по формулам

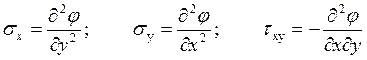.                                       (3)

Поэтому граничные условия (2) принимают вид

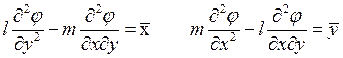.                                (4)

Зная усилия, распределенные вдоль границы, можем с помощью интегрирования уравнений (4) найти функцию  на границе.

Таким образом, задача о напряженном состоянии в плоской пластинке сводится к определению функции , которая удовлетворяет уравнению (1) в каждой точке внутри области, а на границе принимает вместе со своими первыми производными заданные значения.

Используя метод конечных разностей, запишем бигармоническое уравнение (1) для случая квадратной сетки с шагом  в конечно-разностной форме.

Производные можно заменить по формулам

;    ;

;

;                ;

;                .

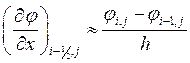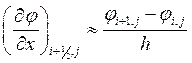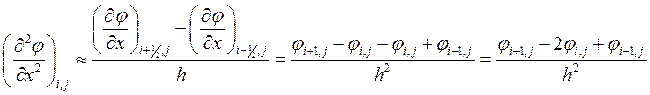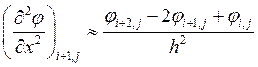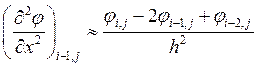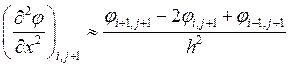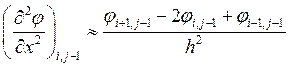Откуда

.

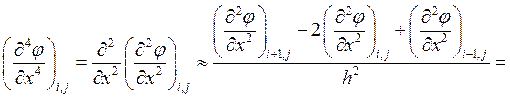
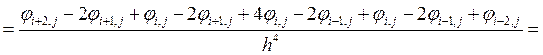
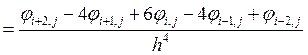Аналогичным образом

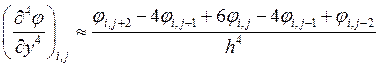
и

.

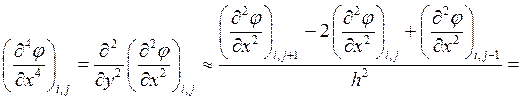
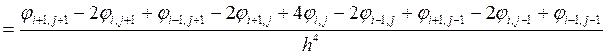Используя полученные формулы численного дифференцирования, преобразуем выражение (1) к виду

. (5)

Это уравнение должно удовлетворятся в каждой узловой точке сетки внутри пластинки.

Чтобы найти граничные значения функции , проинтегрируем уравнение (4).

Учитывая, что

;

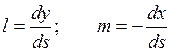где  – элемент дуги границы, запишем уравнение (4) в следующей форме:

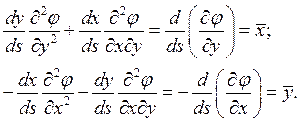                                           (6)

После интегрирования этих равенств получим

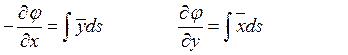                                  (7)

Теперь воспользуемся уравнением

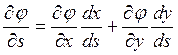, которое после интегрирования по частям дает

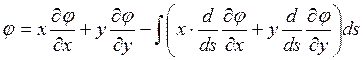.                                     (8)

Подставляя в равенство (8) значения производных, определяемых формулами (6) и (7), можем найти граничные значения . Следует заметить, что при определении первых производных по формулам (7) появятся две постоянные интегрирования  и , а интегрирование в равенстве (8) введет третью постоянную , в силу чего окончательное выражение для  будет содержать линейную функцию . Поскольку компоненты напряжений представляются вторыми производными от функции , эта линейная функция не повлияет на распределение напряжений, и постоянные  можно выбрать произвольно.

Отыскав приближенные значения  в узловых точках границы (или вблизи границы) и выписав для остальных узловых точек, расположенных внутри области, уравнения в форме (5), получим систему линейных уравнений, достаточную для определения всех узловых значений функции . Затем для приближенного вычисления напряжений по формулам (3) можно использовать разностные отношения

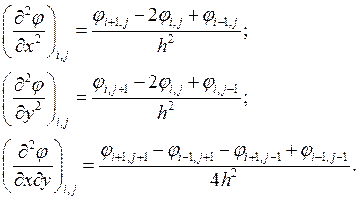                                      (9)

Рассмотрим квадратную пластинку, нагруженную, как показано на рисунке 1.

В рассматриваемой задаче имеет место симметричное нагружение пластинки. Выбрав координатные оси согласно рисунку, определим граничные значения функции .

От  до  к границе пластинки не приложено усилий. Отсюда  и =0, т.е.

.

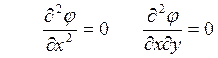Интегрирование этих уравнений дает

.

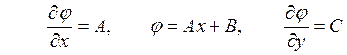Здесь   – постоянные вдоль оси  и, как отмечалось ранее, их можно выбирать произвольно. Положим

.

Тогда функция  вдоль ненагруженной части стороны пластинки обращается в нуль, что обеспечивает симметрию функции  относительно оси у.

От  и до  на нижней стороне пластинки действует равномерно распределенная нагрузка интенсивностью , и уравнения (7) дают

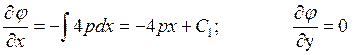
Повторное интегрирование дает

.

Постоянные интегрирования определим из условия, что для точки (), общей для обеих частей границы, значения  и , вычисленные слева и справа, должны совпадать. Отсюда

, и получаем .

На участке нижней границы от  до  имеем

.                                      (10)

В углу пластинки получаем

,                .

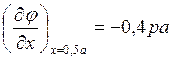Вдоль вертикальной стороны пластинки  усилий не приложено, и, исходя из уравнений (7), заключаем, что вдоль этой стороны значения  и  должны быть такими, как и в нижнем левом углу, т.е.

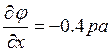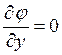,                 .                                                       (11)

Отсюда следует, что вдоль вертикальной стороны пластинки функция  остается постоянной. Эта постоянная должна быть равна , как было найдено выше для нижнего угла.

Вдоль ненагруженной части верхней стороны пластинки первые производные от  остаются постоянными и будут иметь те же значения (11), которые вычислены для верхнего угла. Таким образом, на ненагруженной верхней части пластины имеем

.

Поскольку в верхнем левом углу , приходим к выводу, что , и тогда