



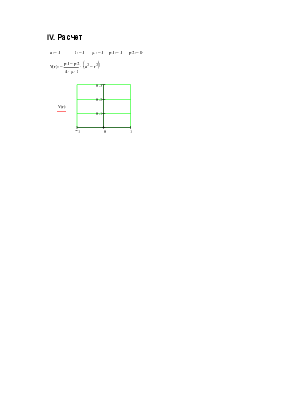
Министерство общего и профессионального образования РФ
Тульский государственный университет
Кафедра прикладной математики и информатики
Лабораторная работа №3
Ламинарное течение несжимаемой вязкой жидкости в цилиндрической трубе
|
Выполнил: |
ст. гр. 520281 |
|
|
Проверил: |
доц. |
Тула 2001
Ламинарное течение несжимаемой вязкой жидкости в цилиндрической трубе
Построение математической модели процесса ламинарного течения несжимаемой вязкой жидкости в цилиндрической трубе; получение аналитического решения поставленной задачи; проведения численных исследований.
1. Построить математическую модель процесса ламинарного течения несжимаемой вязкой жидкости в цилиндрической трубе.
2. Получить аналитическое решение задачи.
3. Построить профиль скоростей течения в сечении трубы.
Исследуем ламинарное течение в цилиндрической трубе радиуса а. Пусть вязкая несжимаемая жидкость течет вдоль трубы. Движение вязкой несжимаемой жидкости описывается системой уравнений, состоящей из уравнений Навье-Стокса и уравнения неразрывности:
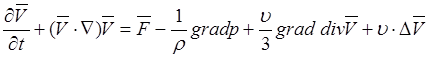 ;
(1)
;
(1)
![]() ,
(2)
,
(2)
где ![]() - скорость жидкости;
- скорость жидкости; ![]() - давление;
- давление; ![]() -
плотность;
-
плотность; 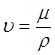 - кинематический коэффициент
вязкости;
- кинематический коэффициент
вязкости; ![]() - коэффициент вязкости;
- коэффициент вязкости; ![]() - массовая сила, отнесенная к единице
массы.
- массовая сила, отнесенная к единице
массы.
Будем полагать, что массовые силы отсутствуют, течение стационарно и в каждой точке скорость направлена параллельно оси трубы.
Для решения задачи воспользуемся цилиндрической
системой координат ![]() ,
, ![]() ,
,
![]() , причем, ось трубы примем за ось
, причем, ось трубы примем за ось ![]() .
.
Граничные условия задачи (условия прилипания) имеют вид:
![]() .
(3)
.
(3)
Таким образом, уравнения (1)-(3) представляют собой математическую модель задачи о течении вязкой несжимаемой жидкости в цилиндрической трубе.
С учетом сделанных предположений запишем уравнения (1) и (2) в цилиндрической системе координат:
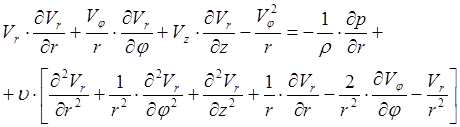
![]()
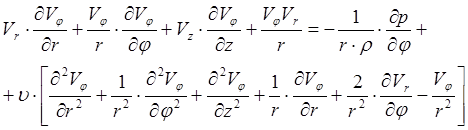 (4)
(4)
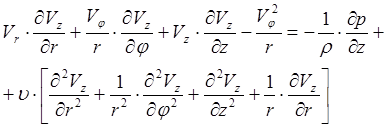
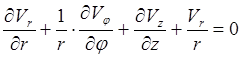 .
.
Так как имеем ![]() ;
; ![]() ,
то система (4) принимает вид:
,
то система (4) принимает вид:
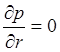 ;
;
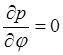 ;
; 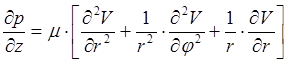 ;
;
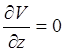 . (5)
. (5)
Первые два
уравнения системы (5) показывают, что ![]() может
зависеть только от
может
зависеть только от ![]() . Последнее уравнение
показывает, что
. Последнее уравнение
показывает, что ![]() есть функция только
есть функция только ![]() и
и ![]() .
Так как правая часть третьего уравнения не зависит от
.
Так как правая часть третьего уравнения не зависит от ![]() ,
то и левая часть не может зависеть от
,
то и левая часть не может зависеть от ![]() .
Следовательно,
.
Следовательно, 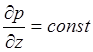 .
.
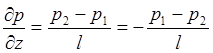 ,
(6)
,
(6)
где ![]() и
и ![]() - давления в двух точках на оси
- давления в двух точках на оси ![]() , отстоящих одна от другой на
расстоянии l соответственно.
, отстоящих одна от другой на
расстоянии l соответственно.
Функция ![]() удовлетворяет
уравнению
удовлетворяет
уравнению
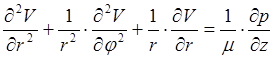 (7)
(7)
и граничному условию на стенке трубы, которое принимает вид
![]() .
(8)
.
(8)
Если ![]() ,
то уравнение (7) перепишем в виде
,
то уравнение (7) перепишем в виде 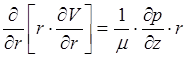 .
.
Интегрируя, получаем 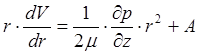 .
.
Производя деление последнего уравнения на ![]() и еще раз интегрируя по
и еще раз интегрируя по ![]() , находим:
, находим:
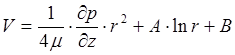 .
.
Произвольные постоянные А и В определяются
из граничного условия (8) и дополнительного условия, которое заключается в том,
что скорость ![]() остается ограниченной во всей
рассматриваемой области течения.
остается ограниченной во всей
рассматриваемой области течения.
Для выполнения дополнительного условия
следует положить А=0. Из условия (8) находим 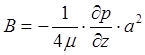 .
Тогда
.
Тогда
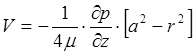 .
(9)
.
(9)
Никакого другого решения задачи не существует. Действительно, положим
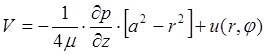 .
.
Подставим это выражение в уравнения (7) и
(8). Получим, что функция ![]() должна удовлетворять
условию
должна удовлетворять
условию
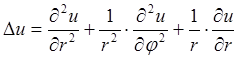 , т. е. должна быть гармонической функцией и,
кроме того, должна удовлетворять условию
, т. е. должна быть гармонической функцией и,
кроме того, должна удовлетворять условию ![]() .
Но гармоническая функция достигает своего максимума и минимума на границе
области определения. Следовательно, в данном случае
.
Но гармоническая функция достигает своего максимума и минимума на границе
области определения. Следовательно, в данном случае ![]() .
.
С учетом выражения (6) формула (9) принимает вид
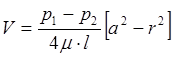 .
(10)
.
(10)
Отсюда видно, что распределение скорости подчиняется параболическому закону.
Рассмотренное течение называется течением Пуазеля.
Полученное решение задачи справедливо лишь для ламинарной формы течения. Определяющим фактором при переходе ламинарного течения в турбулентное является число Рейнольдса, которое в рассматриваемом случае определяется следующим образом:
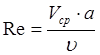 , где
, где ![]() -
средняя скорость течения. Причем существует критическое течение
-
средняя скорость течения. Причем существует критическое течение ![]() , такое, что при
, такое, что при ![]() течение будет ламинарным, а при
течение будет ламинарным, а при ![]() течение будет турбулентным.
течение будет турбулентным.
Движение жидкости будет ламинарным, если скорости течения достаточно малы, или диаметр трубы достаточно мал, или жидкость достаточно вязка.
Опытами установлено, что для течений в цилиндрических трубах критическое число Рейнольдса примерно равно 1000 – 2000.
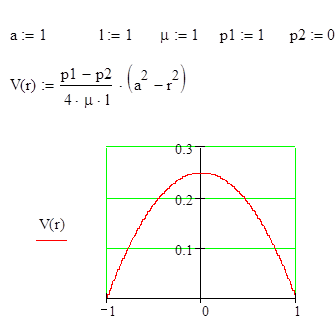
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.