



ЛАБОРАТОРНАЯ РАБОТА N 5
1.Цель и задачи.
Научиться строить гистограмму распределения случайной величины и сопоставлять ее с плотностью.
2.Теоретические сведения.
Пусть X - случайная величина, принимающая значения на отрезке [a,b]..
Разобъем отрезок на nr частей (для простоты равных) и подсчитаем вероятность попадания случайной величины в каждую из них
![]()
![]()
Ступенчатая функция, принимающая на промежутке [a+(i-1)h,a+ih)
значение ![]() /h,
называется гистограммой распределения случайной величины X.
/h,
называется гистограммой распределения случайной величины X.
Промежутки [a+(i-1)h,a+ih);i=1,2,...,nr называются разрядами
гистограммы, площадь прямоугольника, построенного на i-том
промежутке равна ![]() ,сумма всех площадей равна 1. Гистограмма является
приближением плотности случайной величины X : при
,сумма всех площадей равна 1. Гистограмма является
приближением плотности случайной величины X : при
![]() последовательность гистограмм
сходится к плотности (как минимум в среднем, при
непрерывной плотности - равномерно).
последовательность гистограмм
сходится к плотности (как минимум в среднем, при
непрерывной плотности - равномерно).
Если X - известная случайная величина, то гистограмма фактически не нужна.
Иное дело, когда X неизвестна, а в нашем распоряжении имеется только выборка наблюдаемых значений X
![]()
В этой ситуации мы может найти частоты попадания
в i-й разряд гистограммы ![]() ,
где
,
где ![]() -количество наблюдаемых
значений, попадающих в i-й разряд, и построить ступенчатую
функцию, принимающую на промежутке
-количество наблюдаемых
значений, попадающих в i-й разряд, и построить ступенчатую
функцию, принимающую на промежутке
[a+(i-1)h,a+ih)
значение ![]() Из закона больших чисел следует,
что она приближается к гистограмме . По виду гистограммы можно сделать
предположение о законе распределения X. и поставить задачу об
определении параметров распределения.
Из закона больших чисел следует,
что она приближается к гистограмме . По виду гистограммы можно сделать
предположение о законе распределения X. и поставить задачу об
определении параметров распределения.
Ниже приводится примерная программа построения гистограммы.
Для обращения к ней необходимо задать число
разрядов nr и массив частот gist[] ,
gist[i]= ![]() ,
i=1,2,...,nr.
,
i=1,2,...,nr.
В программе, приводимой ниже, строится гистограмма нормального распределения, формируемого функцией norm().
Программа 4
# include <stdio.h>
# include <stdlib.h>
# include <conio.h>
# include <math.h>
# include <graphics.h>
/* датчик случайных чисел */
double uni()
{
double dr=rand();
return dr/RAND_MAX;
}
/* имитация нормального распределения */
double norm()
{
int k; double s=-6.0;
for(k=0; k<12; k++) s=s+uni();
if(s>6.0) s=6.0;
return s;
}
/* построение гистограммы */
void gistogramma(double a,double b,int nr,double *gist)
{
int i,j,x1,y1,x2,y2;
int gdriver=DETECT,gmode,maxx,maxy,pole=40;
double dnr=nr,mxg,mx,my;
/* установка графического режима*/
initgraph(&gdriver.&gmode,””};
maxx=getmaxx(); maxy=getmaxy();
/* ось абсцисс,подписи и масштабные коэффициенты */
moveto(pole,maxy-pole); lineto(maxx-pole,maxy-pole);
line(pole,maxy-pole-3,pole,maxy-pole+3};
gcvt(a,3,str);outtext(pole-1,maxy-pole+5,str);
line(maxx-pole,maxy-pole-3,maxx-pole,maxy-pole+3};
gcvt(b,3,str);outtext(maxx-pole-1,maxy-pole+5,str);
mx=(maxx-2*pole)/(b-a);
for(i=0,mxg=0;i<nr;i++)if(gist[i]>mxg)mxg=gist[i];
my=(maxy-2*pole)/ mxg;
/* гистограмма */
x1=pole;y1=maxy-pole;moveto(x1,y1);
for(i=0;i<nr;i++) {
x1=(1.0-i/dnr)*pole+(i/dnr)*(maxx-pole);
x2=(1.0-(i+1)/dnr)*pole+((i+1)/dnr)*(maxx-pole);
y2=y1-my*gist[i];
lineto(x1,y2); lineto(x2,y2); lineto(x2,y1);
}
getch();
closegraph();
}
main()
{
int i,j,k,n=10000,nr=50;
double s,*gist;
randomize();
gist=malloc(nr*sizeof(double));
for(i=0;i<nr;i++) gist[i]=0;
/* сбор статистки */
for(i=0;i<n;i++) {
j=((6.0+norm())/12.0)*nr;
gist[j]++;
}
s=(nr/12.0)/n;
for(i=0;i<nr;i++) gist[i]=gist[i]*s;
gistogramma(-6.0,6.0,nr,gist);
}
Пояснения к программе 4.
1. Гистограмма строится модулем gistogramma, в который передаются следующие параметры
nr - число разрядов;
gist – адрес массива из nr высот ступенек;
a,b- концы промежутка, на котором задана случайная величина (нужны только для надписей).
2. Массив gist готовится в главной программе путем многократных
"наблюдений" случайной величины (в примере путем ее многократной реализации).
Номер разряда гистограммы, в который попадает конкретное значение x
случайной величины, равен, очевидно, целой части выражения
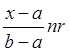
и вычисляется просто в результате присвоения этого выражения целочисленной переменной j.
3. Гистограмма рисуется так, чтобы использовать всю площадь экрана, для чего использует масштабные коэффициенты mx и my.
Задание.
1. Построить гистограмму равномерного распределения (uni()).
2. "Поиграться" с программой 4.изменяя число разрядов,число наблюдений и др..
Оформление отчета.
Отчет должен содержать:
- математическую справку об основных распределениях и графики их плотностей;
- текст своей программы с пояснениями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.