Маятник Максвелла. Внешний вид и параметры лабораторной установки. Определение момента инерции маятника Максвелла

Санкт-Петербургский государственный университет аэрокосмического приборостроения

Рейтинг за работу

Преподаватель           

Отчёт по лабораторной работе №3

по курсу общая физика

«Маятник Максвелла»

ОФ43.2205_1.03_ЛР

Работу выполнил               студент группы 1564 кс

Санкт-Петербург

2005

1. Цель работы: определение момента инерции маятника Максвелла.

2. Описание лабораторной установки.

На вертикальной стойке крепятся два кронштейна. Верхний неподвижный кронштейн снабжён воротком 1 для крепления и регулировки бифилярного подвеса, электромагнитом 2 для фиксирования маятника в верхнем положении и фотодатчиком 3, включающий секундомер. На подвижном кронштейне закреплён фотодатчик 4, включающий секундомер. Шкала секундомера 5 вынесена на лицевую панель прибора.

Кнопка «Сеть» включает питание установки, кнопка «сброс» производит обнуление показаний секундомера. При нажатии на кнопку «Пуск» отключается электромагнит, и маятник приходит в движение.

Массу и момент инерции маятника можно менять при помощи сменных колец, надеваемых на диск. Длина нити должна быть такой, чтобы нижняя кромка маятника была на 1-2 мм ниже оптической оси нижнего фотодатчика. Ось маятника должна быть горизонтальной. Длина нити (высота падения) определяется по шкале, нанесённой на вертикальной стойке.

Параметры установки:

радиус оси R_оси = 5 мм, радиус нити R_нити = 0,6 мм, радиус диска R₁ = 42,5 мм, внешний радиус кольца R₂ = 52,5 мм, масса диска m_D = 125 г, масса первого кольца m₁ = 390 г, масса второго кольца m₂ = 264 г.

Таблица технических характеристик приборов.

θ_h = 2 мм.

θ_t = 0,001 с.

3. Рабочие формулы.

1.) t_ср. = (t₁ + t₂ + … + t_N)/N, где t_ср. – среднее значение времени падения; t₁ – время падения при первом измерении; t_N – время падения при последнем измерении; N – количество измерений.

2.) I = m·(r + r_н)²·[(g·t²/2·h₀) - 1], где I – момент инерции маятника Максвелла; m – масса маятника; r – радиус оси маятника; r_н – радиус нити; g – ускорение свободного падения; t – время падения маятника; h₀ – высота падения маятника.

3.) I_ср.взв. = I₁ + I₂ + … + I_N/N, где I_ср.взв. – среднее взвешенное значение момента инерции.

4.) I_D = m_D·R_D²/2, где I_D – момент инерции диска; m_D – масса диска; R_D - радиус диска.

5.) I_К = m_К·(R_К1² + R_К2²)/2, где I_К – момент инерции кольца; m_К – масса кольца; R_К1 – внутренний радиус кольца; R_К2 – внешний радиус кольца.

6.) I_теор. = [m_D·R₁² + m_К·(R₁² + R₂²)]/2, где I – теоретическое выражение для маятника Максвелла; R₁ – радиус диска; R₂ – внешний радиус кольца.

4. Результаты измерений и вычислений.

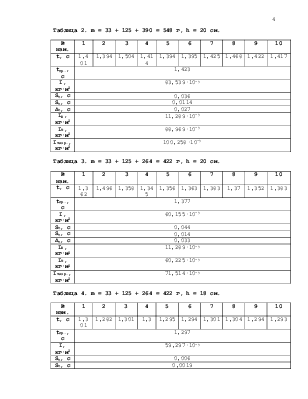
Таблица 1. m = 33 + 125 = 158 г, h = 20 + 1 = 21 см.

Таблица 2. m = 33 + 125 + 390 = 548 г, h = 20 см.

Таблица 3. m = 33 + 125 + 264 = 422 г, h = 20 см.

Таблица 4. m = 33 + 125 + 264 = 422 г, h = 18 см.

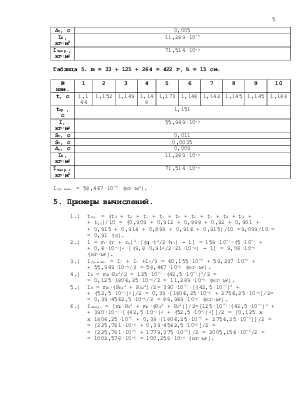
Таблица 5. m = 33 + 125 + 264 = 422 г, h = 15 см.

I_ср.взв. = 58,467·10^-5 (кг·м²).

5. Примеры вычислений.

1.)  t_ср. = (t₁ + t₂ + t₃ + t₄ + t₅ + t₆ + t₇ + t₈ + t₉ +       + t₁₀)/10 = (0,909 + 0,912 + 0,898 + 0,92 + 0,901 +    + 0,915 + 0,914 + 0,899 + 0,916 + 0,915)/10 =9,099/10 = = 0,91 (с).

2.)  I = m·(r + r_н)²·[(g·t²/2·h₀) - 1] = 158·10^-3·(5·10^-3 +   + 0,6·10^-3)²·[(9,8·0,91²/2·21·10^-2) - 1] = 9,08·10^-5 (кг·м²).

3.)  I_ср.взв. = I₃ + I₄ +I₅/3 = 60,155·10^-5 + 59,297·10^-5 +     + 55,949·10^-5/3 = 58,467·10^-5 (кг·м²).

4.)  I_D = m_D·R_D²/2 = 125·10^-3·(42,5·10^-3)²/2 =                 = 0,125·1806,25·10^-6/2 = 11,289·10^-5 (кг·м²).

5.)  I_К = m_К·(R_К1² + R_К2²)/2= 390·10^-3·[(42,5·10^-3)² +           + (52,5·10^-3)²]/2 = 0,39·[1806,25·10^-6 + 2756,25·10^-6]/2= = 0,39·4562,5·10^-6/2 = 88,969·10^-5 (кг·м²).

6.)  I_теор. = [m_D·R₁² + m_К·(R₁² + R₂²)]/2=[125·10^-3·(42,5·10^-3)² + + 390·10^-3·[(42,5·10^-3)² + (52,5·10^-3)²]]/2 = [0,125 x    x 1806,25·10^-6 + 0,39·[1806,25·10^-6 + 2756,25·10^-6]]/2 = = [225,781·10^-6 + 0,39·4562,5·10^-6]/2 =                 = [225,781·10^-6 + 1779,375·10^-6]/2 = 2005,156·10^-6/2 =   = 1002,578·10^-6 = 100,258·10^-5 (кг·м²).

6. Вычисление погрешностей.

1.) S_t = √((t₁-t_ср.)² + (t_N-t_ср.)²/N-1), где S_t – средняя квадратичная погрешность значения времени.

2.) S_t = S_t/√N, где S_t – случайная погрешность удельного сопротивления.

3.) Δ_t = θ_t + kS_t, где Δ_t – полная погрешность удельного сопротивления.

Примеры вычислений:

1.)  S_t = √((t₁-t_ср.)² + (t_N-t_ср.)²/N-1) = √((0,909 - 0,91)² +  + (0,912 - 0,91)²(0,898 - 0,91)² + (0,92 – 0,91)² +     + (0,901 – 0,91)² + (0,915 – 0,91)² + (0,914 – 0,91)² + + (0,899 – 0,91)² + (0,916–0,91)² + (0,915 – 0,91)²/10 -- 1 = √(0,000001 + 0,000004 + 0,000144 + 0,0001 +      + 0,000081 + 0,000025 + 0,000016 + 0,000121 + 0,000036+ + 0,000025/9 = √0,000553/9 = √0,0000614 = 0,0078358 =  = 0,008 (с).

2.)  S_t = S_t/√N = 0,008/√10 = 0,008/3,162 = 0,0025 (с).

3.)  Δ_t = θ_t + kS_t = 0,001 + 2,3·0,0025 = 0,007 (с).

8. Окончательные результаты, их обсуждение или несовпадение.

В данной лабораторной работе были проведены исследования маятника Максвелла; рассчитаны среднее время падения маятника, и по нему момент инерции, проведена обработка результатов измерений; было произведено исследование зависимости момента инерции маятника от высоты, с которой происходит падение маятника.

Из проделанных опытов и вычислений видно, что момент инерции маятника не зависит от высоты падения маятника, так как чем больше высота, тем больше время падения маятника. А на момент инерции маятника влияет масса маятника, радиус оси и радиус нити. Также из формулы для момента инерции маятника Максвелла:

I = m·(r + r_н)²·[(g·t²/2·h₀) - 1] следует, что при изменении высоты меняется и время падения, но соотношение остаётся прежним, поэтому высота не влияет на момент инерции маятника Максвелла.

В лабораторной работе мы рассчитываем момент инерции по двум формулам:

1.) Экспериментальное значение момента инерции:

I = m·(r + r_н)²·[(g·t²/2·h₀) - 1];

2.) Теоретическое выражение для момента инерции маятника:

I_теор. = [m_D·R₁² + m_К·(R₁² + R₂²)]/2.

Моменты инерции, посчитанные по этим формулам, различаются между собой