



ПЕРЕХОД ОТ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
К ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
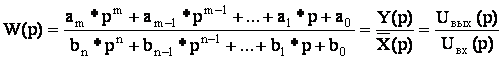
![]()
Оператор Лапласа:
![]()
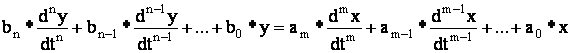
![]()
Решение обратной задачи: от системы уравнений перейти к одному уравнению, в котором присутствуют выходная величина и входная величина.
При этом ![]() заменить
на р.
заменить
на р.
Например:
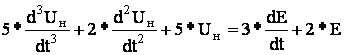
![]()
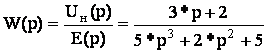
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ НА АВМ
Основные этапы:
1. Составление математической модели объекта (его математическое описание в виде системы дифференциальных уравнений).
2. Приведение уравнений к виду удобному для моделирования.
3. Масштабирование переменных, расчет коэффициентов передачи решающих усилителей и получение уравнений в машинном виде.
4. Составление структурной схемы модели.
5. Набор и настройка модели на АВМ.
6. Пробное решение контрольной задачи.
7. Выполнение программы исследования.
8. Анализ результатов и выводы.
ПРИВЕДЕНИЕ УРАВНЕНИЙ К ВИДУ УДОБНОМУ ДЛЯ МОДЕЛИРОВАНИЯ.
МЕТОД ПОНИЖЕНИЯ ПОРЯДКА ПРОИЗВОДНОЙ
Приведение уравнений к виду удобному для моделирования – это разрешение уравнений системы относительно старшей производной системы уравнений.
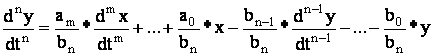
1) В правой части уравнения отсутствуют производные по х.
Например:
![]()
Вид удобный для моделирования:
![]()
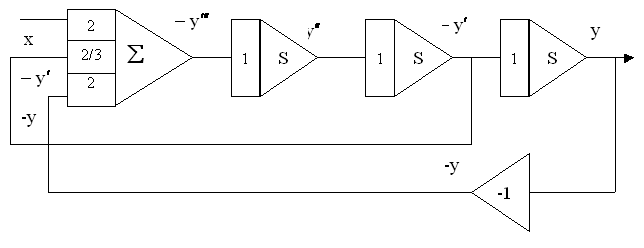
Метод понижения порядка производной, который заключается в том, что с помощью
сумматора реализуется старшая производная выходной величины, а затем путем
последовательного интегрирования получают производные более низких порядков и
саму выходную величину.
2) В правой части уравнения имеются производные по входным величинам.
![]()
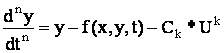
Например:
![]()
где x(t), z(t) – входные величины.
![]()
 |
![]()
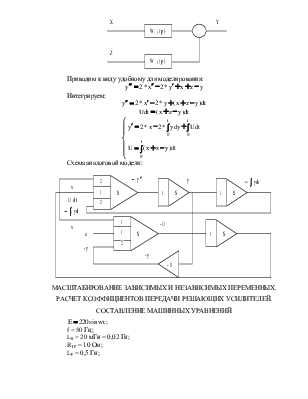
Интегрируем:
![]()
![]()
![]()
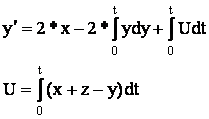
Схема аналоговой модели:
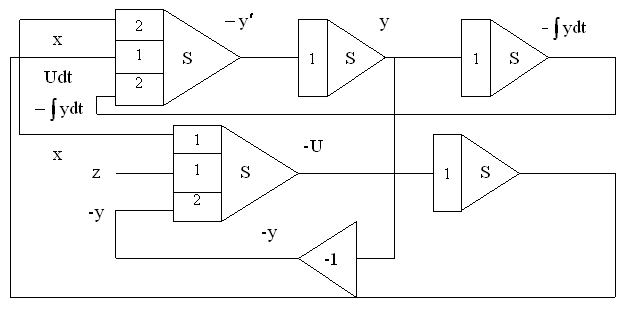 |
РАСЧЕТ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ РЕШАЮЩИХ УСИЛИТЕЛЕЙ.
СОСТАВЛЕНИЕ МАШИННЫХ УРАВНЕНИЙ
![]() ;
;
f = 50 Гц;
LS = 20 мГн = 0,02 Гн;
RТР = 10 Ом;
Lμ = 0,5 Гн;
Rμ = 400 Ом;
Rн = 200 Ом.
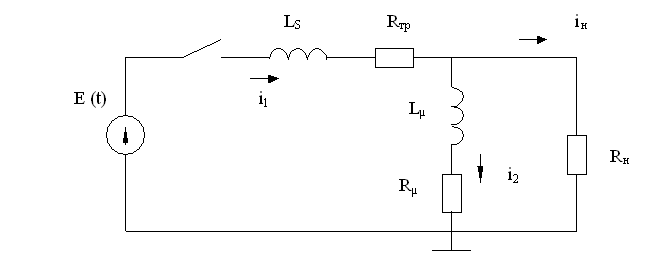
Необходимо разработать аналоговую модель объекта:
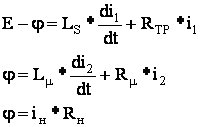
1. Составляем математическое описание цепи, используя метод узловых потенциалов:
![]()
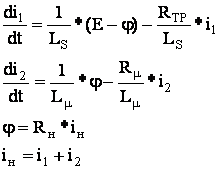
Приводим к виду удобному для моделирования, т.е. решаем относительно старшей производной:
![]()
Операция масштабирования переменных.
Задачи:
1. Приведение всех зависимых переменных к виду напряжений.
2. Величины напряжений не должны превышать максимально допустимой величины для данной АВМ (100 В).
3. Масштабирование независимой переменно (времени) решает задачу удобства наблюдения результатов моделирования при минимальных затратах времени на моделирование.
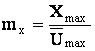

Для определения масштабов определяют максимальные значения переменных. При определении максимальных значений исходят из наиболее жестких режимов для данной цепи. Уточнение – решение контрольной задачи.
1. Umax = Е = 220 В
![]() с-1
с-1
2. imax – режим короткого замыкания в нагрузке:
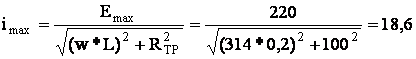 А
А
Принимаем imax = 20 А.
3. Масштабы:
![]()
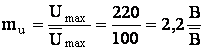
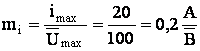
4. Переходим к машинным переменным.
В системе уравнений, описывающих объект, заменим реальные переменные на машинные, умноженные на масштаб.
![]()
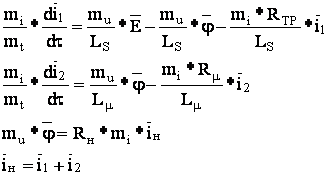
![]() Избавимся от масштабов в левой части:
Избавимся от масштабов в левой части:

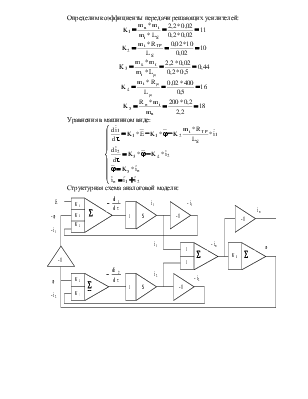
Определим коэффициенты передачи решающих усилителей:
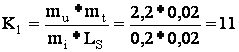
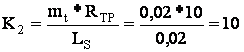
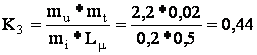
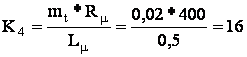
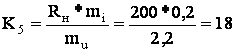
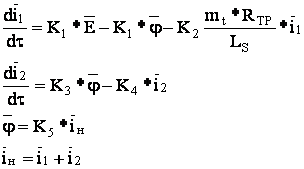
Уравнения в машинном виде:
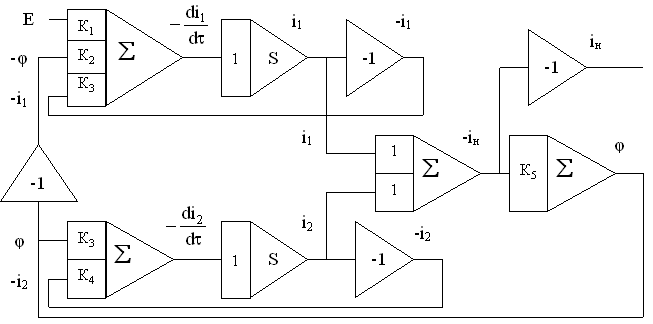 |
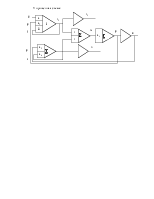
Структурная схема аналоговой модели:
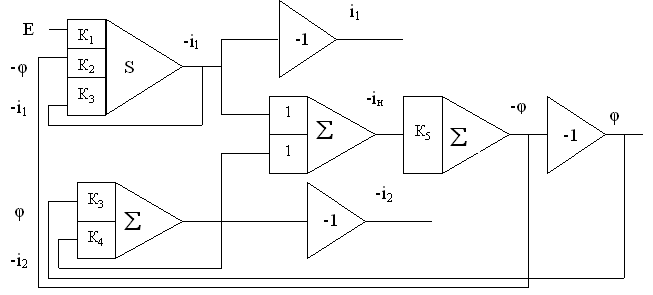 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.