Вимірювання віброакустичних складних сигналів, що містять дискретні складові й суцільну частину в спектральній області з використанням техніки, що робить виміри в 1/3-октавних смугах

Лабораторна робота № 4.

Вимірювання віброакустичних складних сигналів, що містять дискретні складові й суцільну частину в спектральній області з використанням техніки, що робить виміри в -октавних смугах

Мета: засвоєння методичних і практичних навичок, необхідних при проведенні віброакустичних вимірів з використанням техніки, що робить частотний аналіз в -октавних смугах.

Теоретичні відомості

1. Основні поняття

В електроакустиці при вивченні основних властивостей слуху введене поняття висоти звуку, під якою мають на увазі суб'єктивну оцінку сприйняття звуку за частотним діапазоном. Так ширина критичної смуги слуху на середніх і високих частотах приблизно пропорційна частоті й суб'єктивний масштаб сприйняття за частотою близький до логарифмічного закону. Тому за об'єктивну одиницю висоти звуку, що приблизно відбиває суб'єктивне сприйняття, прийнята октава: двократне відношення частот (1; 2; 4; 8; 15; 32 і т.д.). Октаву ділять на частини: напівоктави, третинооктави й т.д. Широко використовується також поняття частотного інтервалу, що становить цілу частку () октави, наприклад, -октавний частотний інтервал [1].

Співвідношення ,  і  для деяких частотних інтервалів приводяться нижче, де  – верхня гранична частота частотного інтервалу [Гц];  – нижня гранична частота часткового інтервалу [Гц];  – центральна частота часткового інтервалу [Гц].

Октава – ;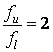

 октави: , ;

 октави: , ;

 октавы: , .

У вимірювальних приладах і приладах, що аналізують, фільтри побудовані таким чином, що ширина смуги пропущення цих фільтрів може регулюватися й відповідати необхідній ширині смуги частотного інтервалу. Супровідний третинооктавный фільтр 1517 містить 41 третинооктавную смугу (фільтрів).

1.1. Спеціальні міркування із приводу частотного аналізу. визначення. ідеальний фільтр

Рис. 4.1. Частотні характеристики ідеального та реального фільтрів

Ідеальним називають смуговий фільтр, що має прямокутну (П-подібну) амплітудно-частотну характеристику, тобто той, що має нульове згасання в смузі пропущення й що загороджує всі частоти поза нею. На рис. 4.1 зіставляються амплітудно-частотні характеристики ідеального й реального фільтрів.

1.2. Ширина смуги пропускання

У той час як ширина смуги пропускання ідеального фільтру може визначатися точно, існують два визначення ширини смуги реального фільтру. Ширина смуги – 3 дб за рівнем половинної потужності, тобто за рівнем спаду пропущеної напруги на 3 дб нижче максимального. Сказане ілюструється на рис. 4.1, де також показана частотна характеристика ідеального фільтру тієї ж ширини смуги.

Ефективна ширина смуги пропущення фільтра (що іноді називається ефективною шириною шумової смуги) – це ширина смуги ідеального фільтру, що пропускає таку ж потужність білого шуму, як і даний фільтр. Октавний і третинооктавний фільтри, застосовувані в пріорі 1617, ґрунтуються на цьому визначенні ширини смуги. Оскільки потужність шумів пропорційна квадрату їхньої напруги, площа під зведеною у квадрат частотною характеристикою реального фільтру (рис. 4.1) дорівнює площі під частотною характеристикою ідеального фільтру при рівності ефективної ширини смуги пропущення ідеального й реального фільтрів.

1.3. Октава й третинооктава

Октавою називають інтервал між двома частотами у відношенні 2:1, тобто

або

де  й  – верхня й нижня частоти, відповідно.

Аналогічним чином, дробова октава визначається співвідношенням

де n – дріб октави. Наприклад,  октави визначається як

З визначення середньої частоти

і ширини смуги пропущення

є наслідком те, що

де К – постійна, залежна від відношення верхньої частоти  до нижнього . Так наприклад, для третинооктави К = 0,231, а для октави К = 0,707. Ширина смуги пропущення фільтра, виражена у відсотках, дорівнює К × 100.

1.4. Частоти фільтрів, що специфікуються

Октавні й третинооктавні фільтри, що застосовуються в приладі 1617, мають середні частоти з ряду кращих частот, що рекомендує МЕК (публікація 225). Цей ряд зв'язує середні частоти з опорною частотою 1000 Гц співвідношенням

де  й т.д.

(За визначенням Американської асоціації зі стандартизації, ASA, , де n – позитивне або негативне ціле число, рівне номеру смуги).

Верхні й нижня граничні частоти смуги,  і , випливають із ефективної ширини смуги фільтра, В, і співвідношення

2. Вимір СКЗ і статистична точність вимірювання

Смуговий фільтр 1617 призначено для аналізу процесів, властивості яких не змінюються в часі. Такі стаціонарні процеси діляться на дві основні групи: детерміновані й випадкові. Детерміновані процеси, параметри яких задані в кожен момент часу, вважають такими, що складаються цілком з дискретних синусоїдальних складових різних частот. Випадкові процеси, що піддаються тільки статистичному визначенню, мають розподілений частотний спектр. Коротше кажучи, детерміновані процеси мають дискретний частотний спектр, а випадкові – безперервний.

Загальна точність будь-якої системи, застосовуваної для виміру середньоквадратичного значення (СКЗ), залежить не тільки від точності самої системи, але й від точності статистичного процесу усереднення стаціонарних сигналів. Для розуміння цих співвідношень варто виходити з визначення СКЗ

де  – час усереднення,  – процес, що змінюється  в часі, і – СКЗ даного процесу за .

З виразу (4.11) треба, що для одержання істинного СКЗ стаціонарного процесу час усереднення повинне бути нескінченно більшим. Оскільки в реальній вимірювальній системі такої умови досягти неможливо, то спостерігається флуктуація СКЗ на стрілочному приладі або іншому відліковому пристрої, причому чим коротше час усереднення, тим сильніше флуктуація.

Виходячи з виразу (4.11), можна також показати, що флуктуація вимірюваного СКЗ стає сильнішою зі зменшенням ширини смуги виміру при незмінному часі усереднення, тобто флуктуація залежить від ширини частотної смуги. Проста оцінка статистичної погрішності СКЗ випадкових процесів дається формулою

де  – похибка; В – ширина смуги виміру або смуга частот вимірюваного процесу (менша з них), Гц;  – час усереднення або тривалість вимірюваного процесу (менше з них), с.

Наведена формула наближена, але дає досить точне значення похибки, якщо добуток ВТ більше 5. Вона дає межі зміни вимірюваного СКЗ із границею вірогідності близько 68%, тобто ймовірність 68% того, що обмірюване СКЗ буде в межах  від істинного СКЗ.

3. Аналіз стаціонарних процесів

При аналізі стаціонарних процесів реальними аналізаторами необхідно враховувати наступні параметри:

1.Час усереднення;

2. Тип запису (запис на постійному або змінному струмі);

3. Швидкість переміщення пера самопису (швидкість запису);

4. Швидкість переміщення стрічки самопису.

4. Час усереднення

Залежно від бажаної точності вимірювання потрібно визначити за формулою (4.12) прийнятний час усереднення випадкових процесів. У табл. 4.1 дане різне стандартне відхилення (у дБ) для ряду значень часу усереднення й частоти. Звичайно нижня границя частот, що аналізуються, спричинює робочий час усереднення. Однак, з ростом частоти на кожні півдекади час усереднення можна знизити в  рази (нормальний крок зміни у вимірювальних підсилювачів фірми Брюль і К’єр). Прилад 1617 має програму керування зміною часу усереднення вимірювальних підсилювачів.