F=ASr(v0-v)1/2/2; N=Nmax; v-? Решение:N=Fv; F= ASr(v0-v)1/2/2;
N=((ASr)/2)×(v02v-2v0v2+v3); N=Nmax; dN/dv=0; dN/dv=((ASr)/2)×
(v02-4v0v+3v2)=0; v02-4v0v+3v2=0; 3v2-4v0v+v02=0;
v1,2=(4v0±(16v02-12v02)1/2)/6=(4v0±2v0)/6; v1=v0 (не eдовл.);
v2=v0/3; v=v2=v0/3 Þ v=v0/3;
Дано: mp=1.67×10-27 кг; v=0.75c; c=3×108 м/с; p-?; T-?; Решение:
p=(mpv)/((1-v2)/c2)1/2; T=((mpc2)/((1-v2)/c2)1/2)-mpc2;
p=5.68×10-19 H×c; T=7.69×10-11 Дж;
8
Дано: n1=4c-1; n2=6c-1; N=50; e-?; Решение: w2=w1-et; w2=2pn2;w1=2pn1;
2pn2=2pn1-et; e=(2p(n1-n2))/t; 2pN=2pn1t-(et2)/2; 2pN=2pn1t-p(n1-n2)t;
t=(2pN)/(2pn1-p(n1-n2));
9
Дано: M=150 кг; L=2.8 м; m=90 кг; S-? Решение: S=v×t(1); Mv-mu=0 Þ v=mu/M(2); u - скорость чел. отн. берега(3) t=S1/u=(L-S)/u;
S1- перемещение чел. относит. берега Подст.(2)и(3) в (1) Þ S=(mu)/M×(L-S)/u=m/M×(L-S)ÞS=(mL)/(m+M)=1.05м.
Дано: m=0.5 кг; v1=1.4 м/c; v’1=1 м/c; Q-?; Решение: T1=(mv21)/2+
+(Jw21)/2; T1=(mv’21)/2+(Jw’21)/2; w=v/R; J=mR2; Q=T1-T2; Q=(mv21)/2+
+(Jw21)/2-(mv’21)/2+(Jw’21)/2=(m/2)×(v21-v’21)+(J/2)×(w21-w’21)=(m/2)×
×(v21-v’21)+1/2mR2((v21/R2)(v’21/R2))=m(v21-v’21) Þ Q=m(v1+v’1)×(v1-v’1)
Дано: m1=10-2 кг; m2=16×10-3 кг; M1=4×10-3 кг/моль; M2=2×10-3; Т=300°K;
p=105 Па; R=8.31Дж/(К×моль); r-? Решение: r=m/V; m=m1+m2;
pV=(m1/M1+m2/M2)RT; V=(m1/M1+m2/M2)×RT/p; r=((m1+m2)p)/
/(m1/M1+m2/M2)RT;
10
Дано: n=10об/с; N=50; A=31.4 Дж; M-?; J-?; Решение: A=Mj; j=2pN;
w0=2pn; M=A/j=A/(2pN); M=Je; e=w0/t=2pn/t; j=w0t-(et2)/2=(w0t)/2;
t=2j/w0=(2×2pN)/2pn=2N/n; J=M/e=MN/pn2; M=0.1 H×м; J=1.59×10-2кг×м2
Дано:m1=7×10-3 кг; m2=2×10-2 кг; M1=28×10-3 кг/моль; M2=4×10-3; g-?
Решение: g=cp/cv; cp=(cp1m1+cp2m2)/(m1+m2);
cv=(cv1m1+cv2m2)/(m1+m2); cv1=(i1/2)×(R/M1);
cv2=(i2/2)×(R/M2); cp1=((i1+2)/2)×(R/M1); i1=3; i2=5;
cp2=((i2+2)/2)×(R/M2); g=(((i1+2)/2)×(R/M1)m1+
((i2+2)/2)×(R/M2)m2)/((i1/2)×(R/M1)m1+(i2/2)×(R/M2)m2)=
=((i1+2)×(m1/M1)+(i2+2)×(m2/M2))/i1(m1/M1)+i2(m2/M2).
11
Дано: m=5×10-3кг; n=0.5 Гц; A=3×10-2 м; x=1.5×10-2 м; v-?; Fmax-?; E-?
Решение: ; v=dx/dt=Awcos(wt+j0);E=Wk+Wp=(mA2w2)/2=
=mA2p2n2=221.8×10-7 Дж; F=ma;F=mAwsin(wt+j0);
x=Acoswt; v=dx/dt=-Awsinwt; a=(a2x/a2w2)=-Aw2coswt; amax=Aw2; Fmax=mamax=mAw2=mA×4p2n2=147.89×10-5=
=1.48×10-3 H; v2/A2w2=1-x2/A2 Þ v2/A2w2=(A2-x2)/A2 Þ
Þ v=((A2w2(A2-x2))A2)1/2=8.1×10-2 м/c.
Дано:m1=m/3; r1=R/2; w2/w1-? Решение: L=const; L=Jw; J1w1=J2w2;
w2/w1=J1/J2; J1=(mR2)/2+(m/3)R2=(5/6)mR2; J2=(mR2)/2+(m/3)×(R/2)2=
=(7/12)mR2; w2/w1=(5mR2×12)/(6×7mR2)=10/7=1.43 Þ w2/w1=1.43.
12
Дано: m1=3 кг; m2=3 кг; M1=40×10-3 кг/моль; M2=28×10-3 кг/моль;cp-?
Решение: DQ=cvmDT; m=m1+m2; DQ=DQ1+DQ2; DQ1=cv1m1DT;
DQ2=cv2m2DT; cvmDT=cv1m1DT+cv2m2DT; cv=(cv1m1+cv2m2)/(m1+m2);
cp=(cp1m1+cp2m2)/(m1+m2); i1=6; i2=5; cp1=((i1+2)/2)×(R/M1);.
cp2=((i2+2)/2)×(R/M2); cp=(R/2)×(((i1+2)m1)/M1+((i2+2)m2)/M2)×
×1/(m1+m2);
13
Дано: l=1м; mпули=m; mшара=100m; a=60°; V-? Решение:
((m+M)u2)/2=(m+M)gh; gh=u2/2;
u=(mV)/(m+M) или u=(mV)/101m=
=V/101; V2/(2×(101)2)=gh; надем h:
BM=l×cosa; h=l-BM; h=l-lcosa=
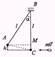 =l(1-cosa), тогда
V=101(2gl(1-cosa))1/2
=l(1-cosa), тогда
V=101(2gl(1-cosa))1/2
Дано: p=aV; g; n; DU-?; A-?; C-? Решение:
DU=Cv(T2-T1)=(Cv/R)(p2V2-p1V1); V2/V1=n;
DU=aV21(n2-1)/(g-1); A=òpdV=(p1/V1)×(V22-V21)=(1/2)×
×aV21(n2-1); aV2=RT; p(dV/dT)=R/2 Þ C=Cv+R/2=
=(R/2)×((g+1)/(g-1)).
14
Дано: r=t3i+3t2j; t=1c; v-?; a-?; Решение: v=dr/dt=(d/dt)×(t3i+3t2j)=3t2i+
+6tj; a=dv/dt=6ti+6j; v=(v2x+v2y)1/2; vx=3t2; vy=6t; v=((3t2)2+(6t)2)1/2;
a=(a2x+a2y)1/2; ax=6t; ay=6; a=((6t)2+62)1/2 Þ v=6.7 м/с; a=8.48 м/с2
Дано: m=1 кг; h=10см; x0=0.5см; F-? Решение:
По закону сохр. Энерг. В момент удара Wn1=Wn2; Wn1=
=mgh; Wn2=(k×x12)/2 Þ mhg=(k×x12)/2; x1=((2mgh)/k)1/2 – деформация пружины весов в момент удара. Mg=F2, где
F2=kx2; По закону Гука x2=x0 Þ mg=kx0; k=(mg)/x0;
Показания весов в момент удара F=mg+F1;
F1=k((2mgh)/k)1/2 – по закону Гука.
![]()
15
Дано: m=5×10-3 кг; V1;V2=2V1; A=103 кДж; <vкв>-? Решение:
A=(m/M)RT×ln(V2/V1) Þ RT/M=A/(m×ln(V2/V1)); <vкв>=((3RT)/M)1/2;
<vкв>=(3A/(mln(V2/V1)))1/2; <vкв>=(3×103/(5×10-3ln2))1/2=930м/с
16
Дано: e=3 рад/с2; t=1c; a=7.5 м/с2; R-? Решение: a=(a2t+a2n)1/2; at=eR;
an=v2/R=w2R=e2t2R; a2=e2R2+e4t4R2=e2R2(1+e2t4); R=a/(e×(1+e3t4)1/2) Þ
Þ R=79см.
Дано: T1=300 K; T2=600 K; h-?
Решение: h=(Q1-Q2)/Q1=(Q12-Q31)/Q12; p=const; dQ=0;
V2/V1=T2/T1; T2V2g-1=T3V3g-1; T1=T3; g=(i+2)/i;
Q31=(nRT1)×ln(V3/V1)=(nRT1)×ln(V3T2/V2T1)=
=(nRT1)×ln[(T2/T1)1/(g-1)×(T2/T1)]=
=(nRT1)×ln(T2/T1)g/(g-1)=(nRT1)×ln(T2/T1)i+2/2=(nRT1)×((i+2)/2)×
×ln(T2/T1); h=((T2-T1)-T1×ln(T2/T1))/(T2/T1) Þ h=30.7%
17
Дано: p=0.5p0; t=10°C; M=29×10-3 кг/моль; h-? Решение: h0=0;
p=p0e-(mg(h-h0))/RT; p/p0=e-(Mgh)/RT; Mgh/RT=-ln(p/p0); h=-(RT)/Mg×ln(p/p0);
h=5.7 км;
18
Дано: m=1кг; p=8×104 Па; r=4 кг/м3; U-?
Решение: U=5/2×m/M×Rt ; pV=m/M× RT Þ p=rRT/M=p/r ;
U= 5/2×mp/r=2.5×104/4=5×104 Дж
Дано: m1=m2=m; v1=v2=v; T2/T1-? Решение: T=(mv2)/2+(Jw2)/2; w=v/R;
J1=(2/5)×mR2; J2=(1/2)×mR2; T1=(mv2)/2+(2/5)mR2×(v2/(2R2))=(7/10)mv2;
T2=(mv2)/2+(1/2)mR2×(v2/(2R2))=(3/4)mv2; T2/T1=1.07
19
Дано: t=60c; n1=5об/с; n2=3об/c; e-?; N-?
Решение: e=dw/dt=2p(n2-n1)/t=-6.28×2/60=-0.2 рад/с2;
Поскольку вращение равномерное, то N=(n1+n2)/2×t=(5+3)/2×60=240 об.
20
Дано: mp=1.67×10-27 кг; v=0.75c; c=3×108 м/с; p-?; T-?; Решение:
p=(mpv)/((1-v2)/c2)1/2; T=((mpc2)/((1-v2)/c2)1/2)-mpc2;
p=5.68×10-19 H×c; T=7.69×10-11 Дж;
Дано: R=0.2 м; J=0.15 кг×м2; m=0.5 кг; h=2.3 м; t-?; T-? Wк-? Решение:
Mgh=(mv2)/2+(Jw2)/2; w=v/R; h=(at2)/2; mg×(at2)/2=(a2t2)/2(m+(J/R2));
a=(mg)/(m+(J/R2)); t=((2h)/2)1/2; TR=Je; T=(Je)/R; e=a/R; T=(Ja)/R2;
Wк=(mv2)/2=(ma2t2)/2 Þt=2c; T=4.31H; Wк=1.32 Дж
Дано: M=32×10-3 кг/моль; i=5; p1=106 Па; V1=5×10-3 м3; V=nV1; n=3;
Q=0; p-?; A-?; Решение: Q=0; A=-DU; pVg=const; p=p1(V1/V)g;
g=(i+2)/i=1.4; p=p1n-g; DU=(m/M)cv(T/T1); A=(m/M)×(i/2)×R(T1-T);
p1V1=(m/M)RT1; pV=(m/M)RT; A=(i/2)(p1V1-pV) Þ p=0.21 МПа;
A=4.63 кДж.
21
Дано: h1=0.8 м; h2=0.72 м; e-? Решение: e=v2/v1; mgh1=(mv21)/2;
mgh2=(mv22)/2; h2/h1=v22/v21=e2; e=(h2/h1)1/2 Þ e=0.95
22
Дано: m=2 кг; a=30°; A=216 Дж; S-?; t-?; Решение: A=mV02/2 Þ
ÞV0=(2A/m)1/2=(2×216/2)1/2»15м/с; S=V02sin2a/g=216sin60°/10=18.7 м;
В наивысшей точке Vy=V0sina-gt/2; t=2V0sina/g=30×0.5/10=1.5 c
Дано: M=32×10-3 кг/моль; i=5; p1=106 Па; V1=5×10-3 м3; V=nV1; n=3;
T=const; p-?; A-?; Решение: T=const; p1V1=pV; p=(p1V1)/V;
A= V1òV2pdV=p1V1V1òV2dV/V=p1V1ln(V/V1) Þ p=0.33 МПа; A=5.5 кДж.
23
Дано: h=30 м; v0=10 м/с; y(x)-?; v-? Решение: x=v0t; t=x/v0; y=(gt2)/2;
y=(g/2)×(x/v0)2=(g/(2v20))x2; v=(v20+g2t2)1/2; h=(gt2)/2; t=((2h)/g)1/2;
v=(v20+2gh)1/2 Þ y=(g/(2v20))x2; v=26.2 м/с.
Дано: m=1; T1=300K; V1=0.5 м3; p2=3p1; M=28×10-3 кг/моль; i=5; V2-?;
T2-?DU-? Решение: g=(i+2)/i;V2=V1(p1/p2)1/g=0.228 м3;
DU=(m/M)×(i/2)×R(T2-T1)=82.4 кДж; T2=T1(p1/p2)(1-g)/g=411К;
24
Дано:m=10-21; T=300K; Dn/n=0.01; k=1.38×10-23Дж/K; g=9.81м/с2;Dz-?
dn=-n0(mg/kT)e-mgz/(kT)dz; n=n0e-mgz/(kT); dn=-(mg)/kdz Þ dz=(-(kT)/mg)×
×(dn/n); Dz=((kT)/mg)×(Dn/n)=0.0042 мм?
25
Дано: m1=m2=m=1кг; m=0.1; a-?; T1-?;T2-? Решение: m1a=T1-Fтр;
m2a=m2g-T2; (T2-T1)R=Je; Fтр=mN=mm1g; J=mR2; e=a/R; (T2-T1)R=
=(mR2×a)/R; m2g-T2=m2a; T1-mm1g=m1a; T2-T1=ma; a=(g(m2-mm1))/(m1+m2=m);
T2=m2(g-a); T1=T2-ma.
a=3.5м/с2; T1=6.3H ; T2=4.5H
Дано:m1=8×10-3 кг; m2=2×10-2 кг; M1=4×10-3 кг/моль; M2=2×10-3; g-?Решение: g=cp/cv; cp=(cp1m1+cp2m2)/(m1+m2); cv=(cv1m1+cv2m2)/
/(m1+m2); cv1=(i1/2)×(R/M1); cv2=(i2/2)×(R/M2);
cp1=((i1+2)/2)×(R/M1); i1=3; i2=5;
cp2=((i2+2)/2)×(R/M2); g=(((i1+2)/2)×(R/M1)m1+
+((i2+2)/2)×(R/M2)m2)/((i1/2)×(R/M1)m1+(i2/2)×(R/M2)m2)=
=((i1+2)×(m1/M1)+(i2+2)×(m2/M2))/
/i1(m1/M1)+i2(m2/M2) Þ g=1.55
Дано: h=8м; x0=0.5м; x1=1; H-? Решение: mg(h+H)=k(H2/2); Разделив
Первое на второе ур-ние => (h+H)/(x1+x0)=H2/x02; h/(x1+x0)+
+H/(x1+x0)=H2/x02; (H2×(x1+x0)-Hx02)/xo2(x1+x0); H2×(x1+x0)-x02H-hx02=0;
Решим данное квадратное ур-ние:
D=x04-4hx02(x1+x0) => H=x02+-(x04-4hx02(x1+x0))1/2; H1=”+” – уд. Усл. H2=”-” не уд. Усл.
26
Дано: h=0.5м; V0=0; V1-? V2-? V3-? V-? Решение:
Систему можно считать замкнутой тк нет трения
Eп=mgh => Eк поступательного движения = (mV2)/2;
Eк вращения те mgh=Jw2/2+(mV2)/2; w=V/R; mgh=
=(V2(mR2+J))/2R2; V=((2mgh)/(m+J/2))1/2;
a)Момент инерции(МИ) Шара J=2/5mR2 =>
=> V1=((2mgh)/(m+2m/5))1/2=(10/7gh)1/2; V1=2.65м/с
b)МИ диска J=(mR2)/2; V2=((2mgh)/(m+m/2))1/2=(4/3gh)1/2;
V2=2.56м/с;
c)МИ обруча J=mR2; V3=((2mgh)/(m+m))1/2=(gh)1/2;
V3=2.21м/с;
d)для теля соскальзывающего без трения mgh=(mV2)/2;
V=(2gh)1/2; V=3.13м/с.
27
28
Дано:m1=7×10-3 кг; m2=2×10-2 кг; M1=28×10-3 кг/моль; M2=4×10-3; g-?
Решение: g=cp/cv; cp=(cp1m1+cp2m2)/(m1+m2);
cv=(cv1m1+cv2m2)/(m1+m2); cv1=(i1/2)×(R/M1); cv2=(i2/2)×(R/M2);
cp1=((i1+2)/2)×(R/M1); i1=3; i2=5;
cp2=((i2+2)/2)×(R/M2); g=(((i1+2)/2)×(R/M1)m1+
+((i2+2)/2)×(R/M2)m2)/((i1/2)×(R/M1)m1+(i2/2)×(R/M2)m2)=
=((i1+2)×(m1/M1)+(i2+2)×(m2/M2))/
/i1(m1/M1)+i2(m2/M2).
29
Дано: l=0.5 м; n= 1 Гц; j-? Решение: ma=T×sinj; a=w2R=w2l×sinj; mg=T×cosj; a/g=(w2l×sinj)/g=sinj/cosj; cosj=g/w2l Þ j=arcos g/(2pn)2l=
=arcos(10/(2×3.14×1)2×0.5)=60°
30
Дано:m=1.7×10-3 кг; M=4×10-3 кг/моль; i=5; n=V2/V1=3; DS-?;
Решение: DS=DS12+DS23; DS12=1ò2dQ12/T; dQ12=0; DS12=0;
DS23=2ò3(m/M)((cpdT)/T)=(m/M)cpln(T3/T2); p=const; T3/T2=V3/V2=
=V1/V2=1/n; cp=((i+2)/2)R; DS=DS23=(m/M)((i+2)/2)Rln(1/n);
31
Дано: i=5; m=0.008 кг; M=32×10-3 кг/моль; V1=10-2 м3; Т1=353 K°;
T2=573 K°; V2=4×10-2 м3; DS-?
Решение: Изменение энтропии при переходе вещества из состояния 1в состояние 2. DS=1ò2 (dQ/dT); dQ=dU+dA=m/M×CvdT+pdV;
PV=m/M×RTÞ p=mRT/MV; Cv=iR/2=2.5R;
DS=T1òT2(m/M×CvdT/T)+V1òV2(mRdV/MV)=
=m/M(Cvln(T2/T1)+Rln(V2/V1));
DS=mR/M×(2.5ln(T2/T1)+ln(V2/V1))=
=8×10-3×8.31/32(2.5ln(573/353)+ln4)=
=5.4Дж/кг
Дано:m=10-2 кг; v=600 м/с; M=5 кг; h-? Решение: mv=(m+M)u;
u=(mv)/(m+M); ((m+M)u2)/2=(m+M)gh; h=u2/(2g)=(mv)2/(2g(m+M)2);
32
Дано: m1=10кг; m2=2кг; a-? Решение: для груза: m2a=m2g-T; для цилиндра:Je=M; 1/2mR2×(a/R)=TR; T=m1a/2; m2a=m2g-m1a/2; a=m2g/m2+
+m1/2=20/2+5=2.86м/с2.
Дано: v1=2 моля; v2=3 моля; M1=32×10-3 кг/моль; M2=44×10-3; g-?
Решение: v=m/M; g=cp/cv; cp=(cp1m1+cp2m2)/(m1+m2); cv=(cv1m1+cv2m2)/(m1+m2);
cv1=(i1/2)×(R/M1); cv2=(i2/2)×(R/M2); cp1=((i1+2)/2)×(R/M1); i1=3; i2=5;
cp2=((i2+2)/2)×(R/M2); g=(((i1+2)/2)×(R/M1)m1+((i2+2)/2)×(R/M2)m2)/
/((i1/2)×(R/M1)m1+(i2/2)×(R/M2)m2)=((i1+2)×(m1/M1)+(i2+2)×(m2/M2))/
/i1(m1/M1)+i2(m2/M2).
33
Дано:TH=3TX;QH=42 кДж; A-? Решение: h=(TH-TX)/TH=
=(QH-QX)/QH=A/QH; 1-1/3=A/Q Þ A=2/3Q=2/3×42=28 кДж.
34
Дано: m1=3 кг; m2=3 кг; M1=40×10-3 кг/моль; M2=28×10-3 кг/моль;cp-?
Решение: DQ=cvmDT; m=m1+m2; DQ=DQ1+DQ2; DQ1=cv1m1DT;
DQ2=cv2m2DT; cvmDT=cv1m1DT+cv2m2DT; cv=(cv1m1+cv2m2)/(m1+m2);
cp=(cp1m1+cp2m2)/(m1+m2); i1=6; i2=5; cp1=((i1+2)/2)×(R/M1);.
cp2=((i2+2)/2)×(R/M2); cp=(R/2)×(((i1+2)m1)/M1+((i2+2)m2)/M2)×
×1/(m1+m2); cp=685,72 Дж/(кг×К) ???
35
Дано: m=0.01кг; T1=253K; T2=373K; DS-? Решение: DS=ò(dQ/T)
Общее изменение энтропии в данном случае складывается из изменений ее в отдельных процессах. При нагревании массы льда m от
T1 до T0=273K; dQ=mCл×dT; DS1=Cп×m×ln(T0/T1). При нагревании льда массы m при T0=273K; DS2=ml/T0; При нагревании воды от T0 до T2
DS3=Cв×m×ln(T2/T0); При испарении воды массы m при
Т2; DS4=rm/T2;
DS=m(Cл×ln(T0/T1)+l/T0+C×ln(T2/T0)+r/T2)=
=0.01(2100×ln(273/253)+(0.33×
×106)/273+4.19×103×ln(373/273)+2.26×106/373)=88Дж/К
Дано: r=0.125 м; at=5×10-3 м/с2; a=45°; t-?; s-? Решение: tga=an/at;
an=v2/r; at=dv/dt=const; v=0ò1atdt=att; tga=v2/(rat)=(at2t2)/(rat)=(att2)/r;
t=((rtga)/at)1/2; s=0òt vdt=0òt attdt=(att2)/2 Þ t=5c; s=6.25 см;
Дано: h=0.5м; V0=0; V1-? V2-? V3-? V-? Решение:
Систему можно считать замкнутой тк нет трения
Eп=mgh => Eк поступательного движения = (mV2)/2;
Eк вращения те mgh=Jw2/2+(mV2)/2; w=V/R; mgh=
=(V2(mR2+J))/2R2; V=((2mgh)/(m+J/2))1/2;
a)Момент инерции(МИ) Шара J=2/5mR2 =>
=> V1=((2mgh)/(m+2m/5))1/2=(10/7gh)1/2; V1=2.65м/с
b)МИ диска J=(mR2)/2; V2=((2mgh)/(m+m/2))1/2=(4/3gh)1/2;
V2=2.56м/с;
c)МИ обруча J=mR2; V3=((2mgh)/(m+m))1/2=(gh)1/2;
V3=2.21м/с;
d)для теля соскальзывающего без трения mgh=(mV2)/2;
V=(2gh)1/2; V=3.13м/с.
36
Дано: m=0.2 кг; m1=0.3 кг; m2=0.5кг; T1-?; T2-? Решение: m1a1=
=T1-m1g; m2a=m2g-T2; (T2-T1)R-Je; J=(mR2)/2; e=a/R; (T2-T1)R=
=(mR2)/2×(a/R); T2-T1=(ma)/2; T2-T1=m2g-m2a-m1a-m1g; ma+2m2a+2m1g=
=2m2g-2m1g; a=((m2-m1)g)/(m1+m2+(m/2)); T2=m2(g-a); T1=m1(g+a);
Дано: V=50л; Dp=5×105 Па; Q-? Решение: Q=DU+A; A=pDVV=CONST=0;
Q=DU; DU=(m/M)×(i/2)RDT; p1V=(m/M)RT1; p2V=(m/M)RT2; p2V-p1V=
=(m/M)RT2-(m/M)RT1; DpV=(m/M)RDT; Q=(m/M)×(i/2)RDT=(i/2)VDp; i=5;
37
Дано:m=1.7×10-3 кг; M=4×10-3 кг/моль; i=5; n=V2/V1=3; DS-?;
Решение: DS=DS12+DS23; DS12=1ò2dQ12/T; dQ12=0; DS12=0;
DS23=2ò3(m/M)((cpdT)/T)=(m/M)cpln(T3/T2); p=const; T3/T2=V3/V2=
=V1/V2=1/n; cp=((i+2)/2)R; DS=DS23=(m/M)((i+2)/2)Rln(1/n);
38
Дано: m=0.01кг; T1=253K; T2=373K; DS-? Решение: DS=ò(dQ/T)
Общее изменение энтропии в данном случае складывается из изменений ее в отдельных процессах. При нагревании массы льда m от
T1 до T0=273K; dQ=mCл×dT; DS1=Cп×m×ln(T0/T1). При нагревании льда массы m при T0=273K; DS2=ml/T0; При нагревании воды от T0 до T2
DS3=Cв×m×ln(T2/T0); При испарении воды массы m при Т2; DS4=rm/T2;
DS=m(Cл×ln(T0/T1)+l/T0+C×ln(T2/T0)+r/T2)=
=0.01(2100×ln(273/253)+(0.33×
×106)/273+4.19×103×ln(373/273)+2.26×106/373)=88Дж/К
39
40
Дано: i=5; m=0.008 кг; M=32×10-3 кг/моль; V1=10-2 м3; Т1=353 K°;
T2=573 K°; V2=4×10-2 м3; DS-?
Решение: Изменение энтропии при переходе вещества из состояния 1в состояние 2. DS=1ò2 (dQ/dT); dQ=dU+dA=m/M×CvdT+pdV;
PV=m/M×RTÞ p=mRT/MV; Cv=iR/2=2.5R;
DS=T1òT2(m/M×CvdT/T)+V1òV2(mRdV/MV)=
=m/M(Cvln(T2/T1)+Rln(V2/V1));
DS=mR/M×(2.5ln(T2/T1)+ln(V2/V1))=8×10-3×8.31/32(2.5ln(573/353)+ln4)=
=5.4Дж/кг
41
42
Дано: m1=64×10-3 кг; m2=56×10-3 кг; M1=32×10-3 кг/моль; M2=28×10-3; T=300K; R=8.31 Дж/(K×моль); p=2×105 Па; r-? Решение: r=m/V; m=m1+m2; pV=((m1/M1)+(m2/M2))RT; V=((m1/M1)+(m2/M2))×(RT/p);
r=((m1+m2)p)/((m1/M1)+(m2/M2));
43
44
45
46
Дано: DS=4.19кДж/К; DТ=200К; A-? Решение: DS=ò(dQ/T)=Q/Tн Þ
Тн=Q/DS; h=(Тн-Тх)/Тн=DТ×DS/Q; h=A/Q; DТ×DS/Q=A/Q Þ A=DТ×DS=
=200×4.19=838кДж.
47
48
Дано: m1=1 кг; T2=273К°; T1=373K°; m2-? Решение:
КПД идеальной холод. маш. h=T2/(T1-T2)=2.73; кол-во тепла отдав. холодильнику Q2=lm2; l=355кДж/кг; кол-во тепла приним. кипятильником Q1=rm1; r=2.26МДж/кг; h=Q2/(Q1-Q2); h=(Q1-Q2)=Q2 или
hQ1-hQ2=Q2 => Q1=(Q2(1-h))/h или rm1=(lm2(1-h))/h;
m2=(rm1h)/(l(1/h)) => m2=4.94 кг.
49
Дано:V=0.5л=5×10-2м3; m=1г; t=1000°C; pc=93.3 кПа;
M=0.254 кг/моль; a-? Решение: В резулт. диссоц. получ. n1=(2am)/M – атомарного йода; n2=((1-a)×m)/M – молекулярного йода; Их парциальное давление: p1=(2amRT)/(MV); p2==((1-a)mRT)/(MV); По закону Дальтона pc=p1+p2 => pc=((mRT)/(MV))×(1+a) =>
=> a=(MpcV)/(mRT)-1 => a=0.12.
50
51
52
Дано: r=0.125 м; at=5×10-3 м/с2; a=45°; t-?; s-? Решение: tga=an/at;
an=v2/r; at=dv/dt=const; v=0ò1atdt=att; tga=v2/(rat)=(at2t2)/(rat)=(att2)/r;
t=((rtga)/at)1/2; s=0òt vdt=0òt attdt=(att2)/2 Þ t=5c; s=6.25 см;
53
54
Дано:m=28×10-3 кг; M=28×10-3 кг/моль; i=5; n=V2/V1=2; DS-?;
Решение: DS=DS12+DS23; DS12=1ò2dQ12/T; dQ12=0; DS12=0;
DS23=2ò3(m/M)((cpdT)/T)=(m/M)cpln(T3/T2); p=const; T3/T2=V3/V2=
=V1/V2=1/n; cp=((i+2)/2)R; DS=DS23=(m/M)((i+2)/2)Rln(1/n)=-20.2Дж/K
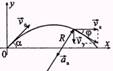
Дано: v0=10м/с; a=45°; R-?; t=1c;Решение:vy=v0sina-gt1;
vy=0 => v0sina=gt1 => t1=(v0sina)/g; t1=0.7; те. При t=1 тело спускается => vx=v0sina; an=v2/R; v=(v2x+v2y)1/2;
an=g×sinj; sinj=vx/(v2x+v2y)1/2 => an=g(vx/(v2x+v2y)1/2) и
R=v2/an=((v2x+v2y)×(v2x+v2y)1/2)/(vx×g); vx=v0cosa=5×(2)1/2м/с;
vy=g(t-t1)=3 м/с; R»6.3м.
55
56
Дано: m=64×10-3кг; M=32×10-3 кг/моль; i=5; n=T2/T1=2; DS-? Решение:
p=const; v=m/M; dQ=nCpdT; vCp=((i+2)/2)R; DS2=1ò2dQ/T=T1òT2ncp(dT/T)=
=ncpln(T2/T1); DS2=n((i+2)/2)Rln(T2/T1)=n((i+2)/2)Rlnn
57
Дано: M=32×10-3 кг/моль; i=5; p1=106 Па; V1=5×10-3 м3; V=nV1; n=3;
Q=0; p-?; A-?; Решение: Q=0; A=-DU; pVg=const; p=p1(V1/V)g;
g=(i+2)/i=1.4; p=p1n-g; DU=(m/M)cv(T/T1); A=(m/M)×(i/2)×R(T1-T);
p1V1=(m/M)RT1; pV=(m/M)RT; A=(i/2)(p1V1-pV) Þ p=0.21 МПа;
A=4.63 кДж.
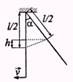
Дано: l=1м; v=5м/с; a-? Решение: Eп=mgh; Eп=> Eк вращения mgh=(Jw2)/2; h=l/2-l/2×cosa=l/2×(1-cosa); мом.
инерции найдем по теореме Штейнера: J=(1/12)ml2+m×
×(l/2)2=(1/3)ml2; w=v’/(l/2); v’-скорость прохождения равновесия центра масс; v’=v/2 => w=v/l; (mg)l/2(1-cosa)
=(mv2l2)/6l2; gl(1-cosa)=(mv2)/3; cosa=1-(v2/3gl); cosa=0.15; a=81°.
58
Дано: m=0.01кг; T1=253K; T2=373K; DS-? Решение: DS=ò(dQ/T)
Общее изменение энтропии в данном случае складывается из изменений ее в отдельных процессах. При нагревании массы льда m от
T1 до T0=273K; dQ=mCл×dT; DS1=Cп×m×ln(T0/T1). При нагревании льда массы m при T0=273K; DS2=ml/T0; При нагревании воды от T0 до T2
DS3=Cв×m×ln(T2/T0); При испарении воды массы m при Т2; DS4=rm/T2;
DS=m(Cл×ln(T0/T1)+l/T0+C×ln(T2/T0)+r/T2)=
=0.01(2100×ln(273/253)+(0.33×
×106)/273+4.19×103×ln(373/273)+2.26×106/373)=88Дж/К
Дано: l=1м; mпули=m; mшара=100m; a=60°; V-? Решение:
((m+M)u2)/2=(m+M)gh; gh=u2/2;
u=(mV)/(m+M) или u=(mV)/101m=
=V/101; V2/(2×(101)2)=gh; надем h:
BM=l×cosa; h=l-BM; h=l-lcosa=
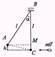 =l(1-cosa), тогда
V=101(2gl(1-cosa))1/2
=l(1-cosa), тогда
V=101(2gl(1-cosa))1/2
59
Дано:i=5; V=2×10 м3; p=1.5×105 Па ; U{W} -?
Решение: U=5/2nRT=5/2pV=5/2×1.5×105×2×10-3=750 Дж
60
Дано: m=2 кг; a=30°; A=216 Дж; S-?; t-?; Решение: A=mV02/2 Þ
ÞV0=(2A/m)1/2=(2×216/2)1/2»15м/с; S=V02sin2a/g=216sin60°/10=18.7 м;
В наивысшей точке Vy=V0sina-gt/2; t=2V0sina/g=30×0.5/10=1.5 c
Дано: M=32×10-3 кг/моль; i=5; p1=106 Па; V1=5×10-3 м3; V=nV1; n=3;
T=const; p-?; A-?; Решение: T=const; p1V1=pV; p=(p1V1)/V;
A= V1òV2pdV=p1V1V1òV2dV/V=p1V1ln(V/V1) Þ p=0.33 МПа; A=5.5 кДж
61
Дано: I=5; m=0.02кг; Q=0; DU=8кДж; T2=900K°; p1=2×105 Па; DT-?
Решение: Кислород 2-х атомный газ. i=5Þg=(i+2)/2=1.4; A=RT1×(m/M)×
×(1-T2/T1)/(g-1)=-RT1×DT/(M(g-1)); Q=DU+A; Q=0ÞDU=-A=m×DT×R/(M(g--1)); DT=M(g-1)DU/(mR)=32×10-3×0.4×8/(0.02×8.31)=0.62K.
T1=T2-DT=899.38; Ур-ние Пуассона Tp(1-g)/g=const; T1p1(1-g)/g= T2p2(1-g)/g;
T1p1-0.4/1.4= T2p2-0.4/1.4; p20.29=p10.29T2/T1; P2=P1×(T2/T1)3.5=2×105×(900/899.38)3.5=2.005×105 Па=200.5 кПа
Дано: Fсопр~v; vуст=80м/с; v=(3/4)×vуст=60м/с; t-? Решение: Тело
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.