Исследование шумовых напряжений резисторов и влияние на их уровень величин сопротивления

Санкт-Петербургский Государственный Политехнический Университет

Кафедра Радиофизики

Отчет о лабораторной работе №19

Флуктуационные колебания в радиофизике.

Выполнили: студенты группы 2093

Смолин Р.В.

Кушнир А.В.

Преподаватель: Зайцев Э.Ф.

Санкт-Петербург 2006г.

Схема измерительной установки

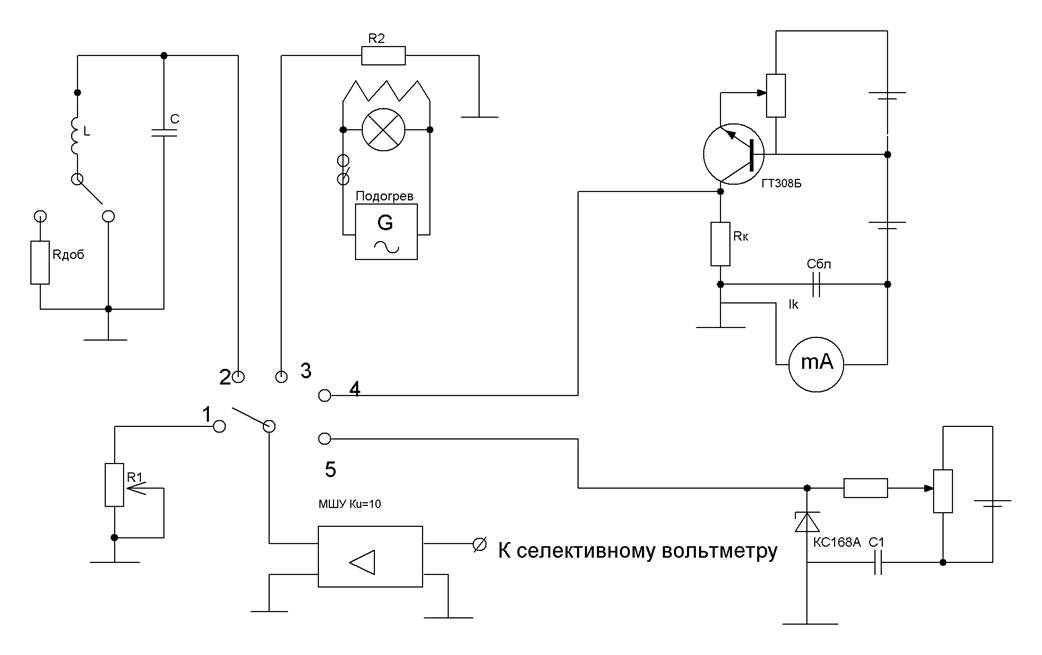
1. Тепловой щум сопротивления

1.1.  Средний уровень напряжения собственного шума усилителя (вместе с микровольтметром) в диапазоне частот 200-600 кГц:  Uсоб=0,42 мкВ

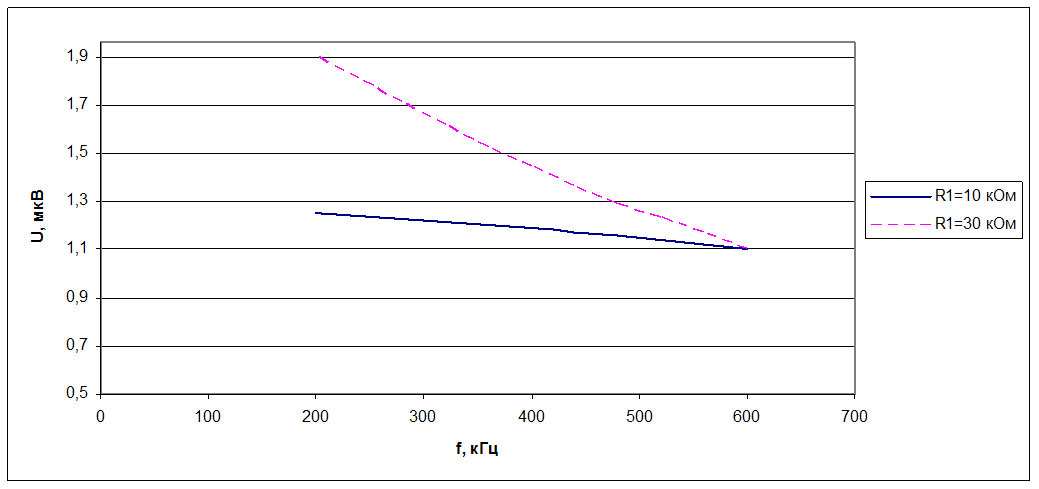
1.2.  Зависимость шумового напряжения от частоты

f, кГц	U, мкВ
	R1=10 кОм	R1=30 кОм
600	0,50	0,53
560	0,52	0,58
520	0,53	0,63
480	0,54	0,63
440	0,58	0,73
400	0,63	0,78
360	0,68	0,83
320	0,73	0,88
280	0,73	0,98
240	0,73	1,03
200	0,73	1,08

Графики экспериментальных зависимостей:

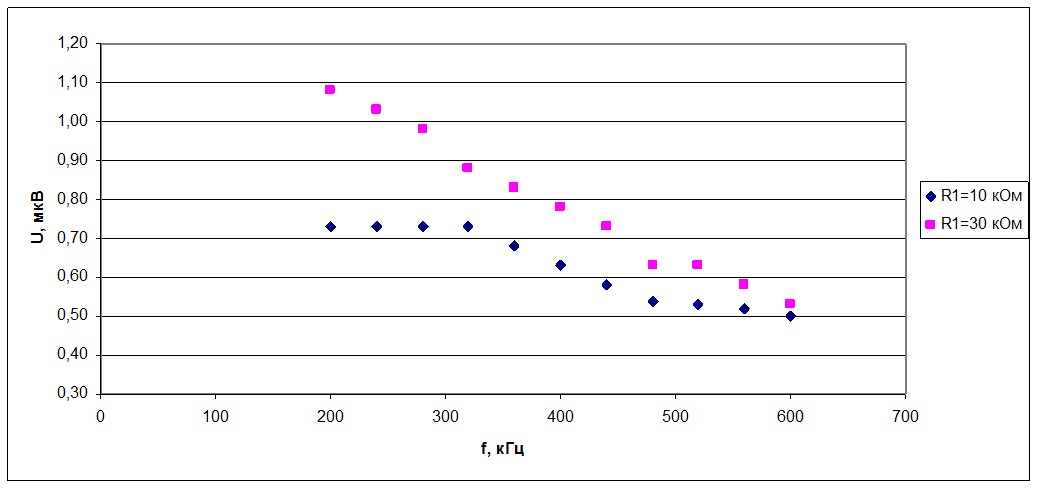
1.3. Зависимость шумового напряжения от величины сопротивления R₁

F=350 кГц

R1, кОм	U, мкВ
5	0,34
8	0,45
10	0,53
15	0,68
20	0,78
30	0,78
47	0,73

 В²

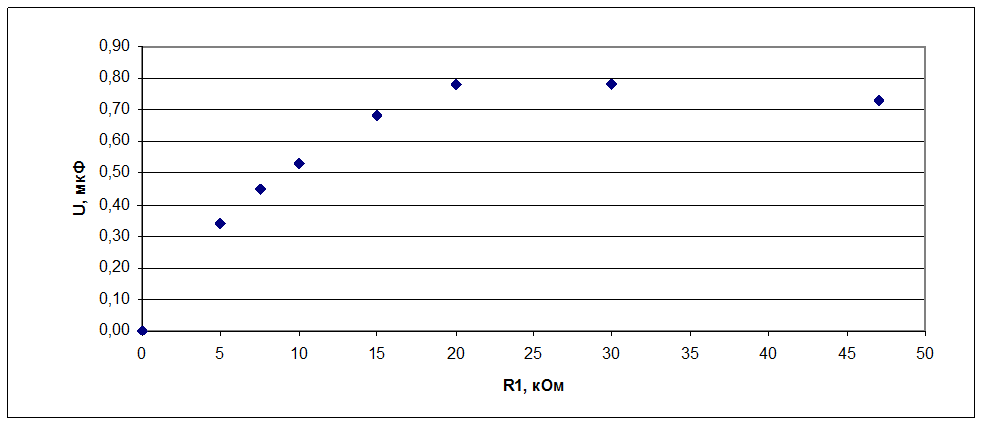
Кривая имеет максимум при R=30 кОм

1.4. Определение значения суммарной параллельной емкости и построение теоретических зависимостей U(f) для R1=10 кОм и 30 кОм

Δf=10 кГц

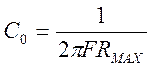=15,2 пФ

Графики теоретических зависимостей 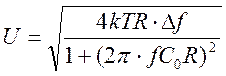 для R1=10 кОм и 30 кОм:

 2. Тепловой шум колебательного контура

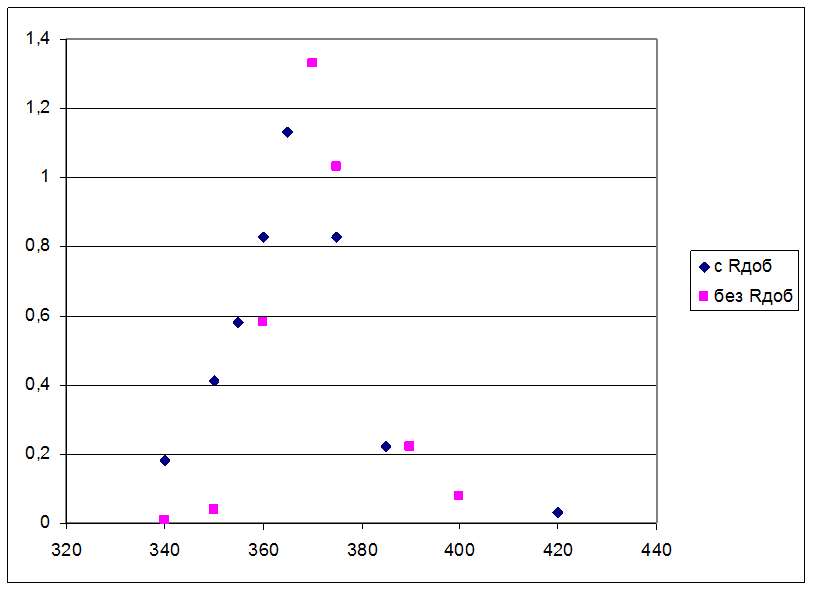
2.1. Измерение зависимости шумового напряжения на LC-контуре от частоты в области резонанса (340 кГц)

С_конт=400 пФ, R_доб=30 кОм

График полученных зависимостей

2.2. Теоретические расчеты величин

Q1(без R_доб)=  ≈370/(375-365)=37

Q2(с R_доб)=  ≈370/(375-360)=25

R₁=Qбез/2πf₀С=39,8 кОм

R₂=Qс/2πfС=26,9 кОм

 

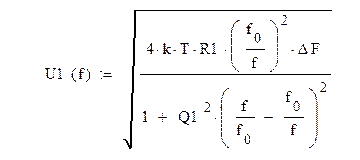
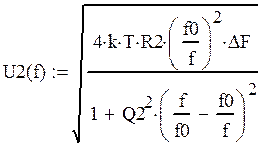
Расчет теоретических значений:

без R_доб U(f₀)=2,5 мкВ

с R_доб U(f₀)=2,1 мкВ

2.3 Расчет среднего квадрата шумового уровня

1) по данным п.2.1. 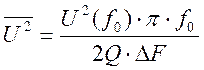=3,24·10^-12 В² (для случая без Rдоб и 3,36·10^-12 В²  с Rдоб)

2) по формуле 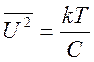=10,1·10^-12 В² 

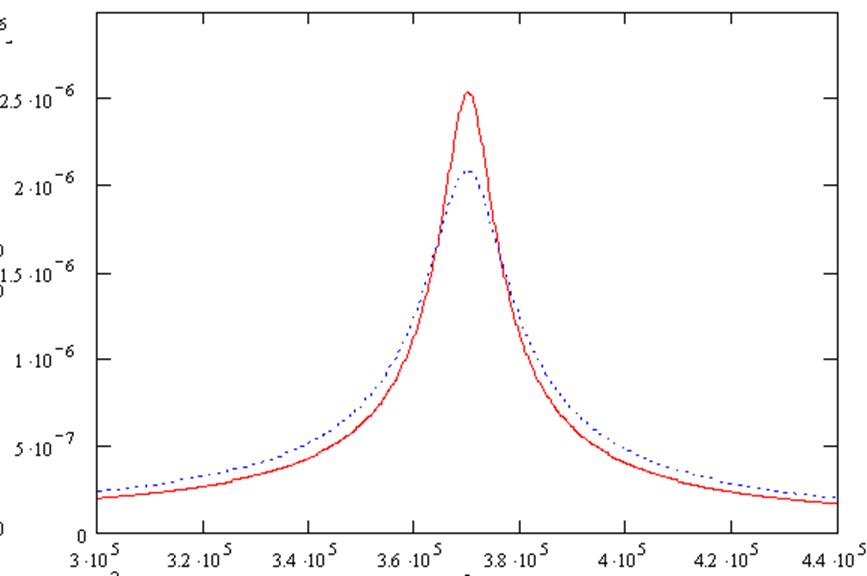
Графики теоретических зависимостей шумового напряжения при наличии (пунктир) и отсутствии (непрерывная) добавочного сопротивления контура

3.1 Измерение шумового напряжения сопротивления при разных температурах

f=350 кГц, R₂=10 кОм

T=T_ком≈20 ⁰С=293К => U=0,47 мкВ

Т=Т_нагр => U=0,56 мкВ

3.2 Расчет неизвестного Т_нагр

Согласно формуле Найквиста: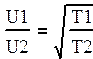

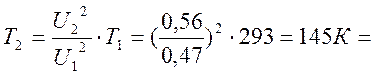142 ⁰С

4. Дробовой шум транзистора.

4.1, 4.3  Зависимость шумового напряжения на коллекторном сопротивлении от тока коллектора

f=200 кГц, r=5 кОм

Теоретическая зависимость:

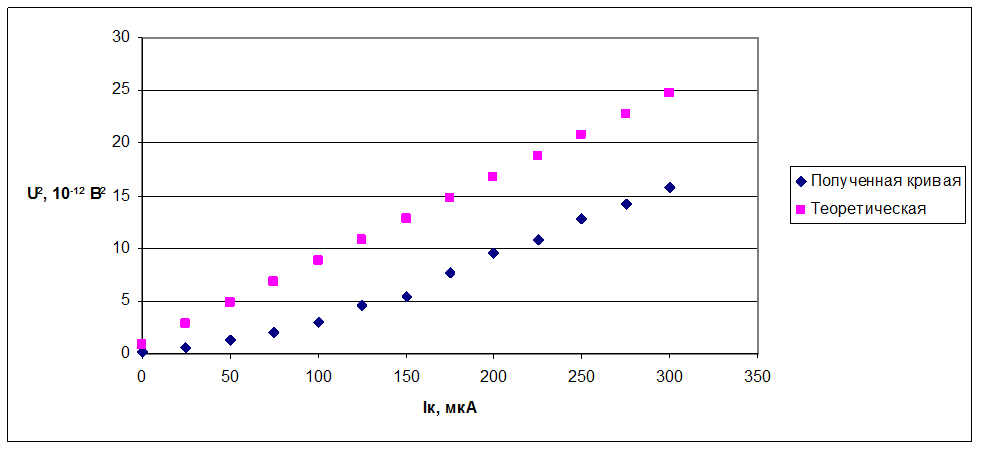
4.2 Широкополосность дробового шума:

Было выяснено, что в частотном диапазоне 200-600 кГц уровень дробового шума БТ остается приблизительно на одном уровне, несколько снижаясь с увеличением частоты:

Для Iк=100 мкА U≈1,63 мкВ

Для Iк=200 мкА U≈2,88 мкВ

5. Шум стабилитрона.

5.1 f=200 кГц

Зависимость шумового напряжения стабилитрона от тока

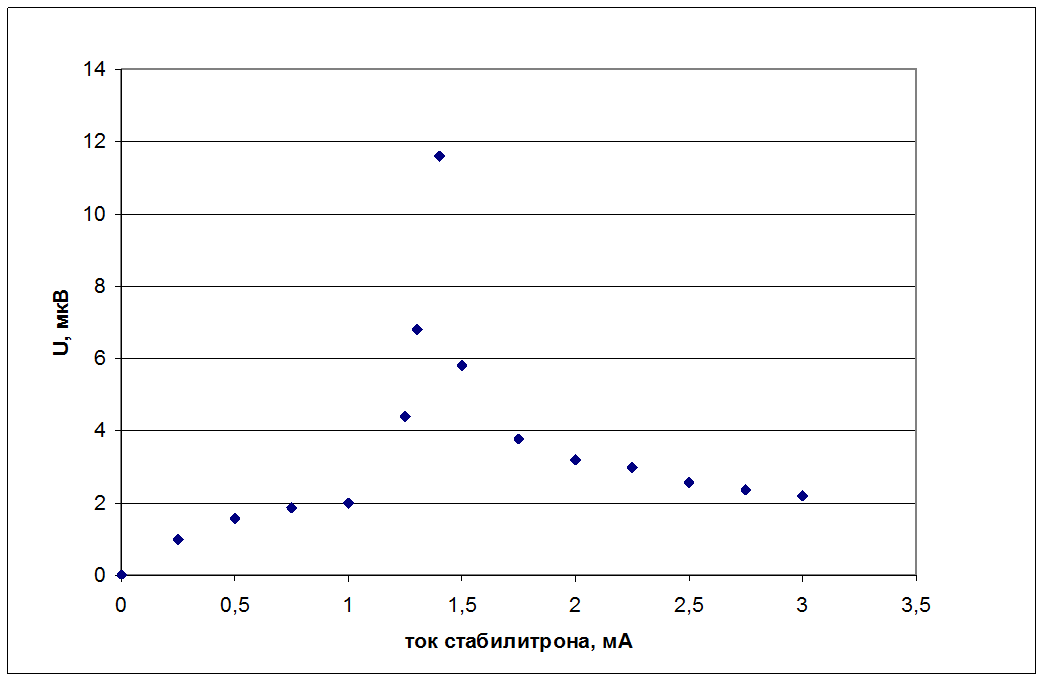Выводы:

В данной лабораторной работе были исследованы шумовые напряжения резисторов и влияние на их уровней величин сопротивления. Как видно из результатов, спектральная плотность интенсивности шума падает с ростом частоты для обоих исследованных значений сопротивления, что объясняется влиянием паразитной емкости. Также, было выяснено, что зависимость уровня шума от сопротивления имеет максимум, исходя из чего найдено значение паразитной емкости с помощью формулы Найквиста. Также было исследовано шумовое напряжение LC-контура: показано, что его зависимость от частоты имеет вид резонансной кривой. Несоответствия  расчетных и теоретических величин добротностей и др. параметров вызваны большой неточностью измерений точек зависимости и нахождения по ним ширины резонансной кривой. Также была получена зависимость уровня шумового напряжения сопротивления коллектора в схеме с БТ от тока коллектора. Видно, что уровень дробового шума БТ заметно выше теплового шума сопротивления. Несоответствие с теоретической кривой вызваны неучтенными паразитными сопротивлениями и неточностью измерений. Также были исследованы шумы лавинного пробоя полупроводникового стабилитрона. Из графика видно, что зависимость уровня шума от постоянного тока стабилитрона имеет резкий пик при Iст=1,4 мА. Начальный рост шумового напряжения связан с ростом спектральной плотности интенсивности шумового тока, а спад объясняется резким уменьшением дифференциального сопротивления с ростом Iст.