Исследование схем комбинационной логики

Санкт-Петербургский Государственный Политехнический Университет

Кафедра Радиофизики

Отчет о лабораторной работе № 30

Цифровые интегральные схемы

Выполнили

                                                                                                    студенты группы 2091/3

                                                                                                                        Семенов Е. А.

                                                                                                                  Каспарович А. А.

                                                                                                                              Проверил

                                                                                                                 Лиокумович Л. Б.

Санкт-Петербург 2005

Введение: Данная работа была проведена нами с целью укрепления знаний, полученных в курсе схемотехники

Пункт №1  Исследование схем комбинационной логики.

Для получения формул, описывающих работу предложенных устройств, нами были составлены карты Карно, минимизировав которые мы получили искомые зависимости.

А) Элемент И-НЕ. В ходе работы была получена следующая  таблица выходного сигнала элемента в зависимости от входных сигналов:

x1	x2	x3	y
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Логика работы элемента описывается формулой:    y=

Б)Элемент ИЛИ-НЕ. В ходе работы получена таблица: Элемент работает по формуле y=

x1	x2	y
0	0	1
0	1	0
1	0	0
1	1	0

В) Элемент И-ИЛИ-НЕ

x1	x2	x3	x4	y
0	0	0	0	1
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

Данное устройство работает по формуле:y=

Г) Схема тайного голосования.  

Таблица истинности:            Работу  схемы можно описать формулой: y=x2*x3+x1*x3+x1*x2

x1	x2	x3	y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Д) Дешифратор двоично-десятичного кода в код 1 из 10

Таблица истинности

x1	x2	x3	x4	y0	y1	y2	y3	y4	y5	y6	y7	y8	y9	Десятичное число
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	1	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	1	0	0	0	0	0	0	0	2
0	0	1	1	0	0	0	1	0	0	0	0	0	0	3
0	1	0	0	0	0	0	0	1	0	0	0	0	0	4
0	1	0	1	0	0	0	0	0	1	0	0	0	0	5
0	1	1	0	0	0	0	0	0	0	1	0	0	0	6
0	1	1	1	0	0	0	0	0	0	0	1	0	0	7
1	0	0	0	0	0	0	0	0	0	0	0	1	0	8
1	0	0	1	0	0	0	0	0	0	0	0	0	1	9
1	0	1	0	0	0	0	0	0	0	0	0	0	0	-
1	0	1	1	0	0	0	0	0	0	0	0	0	0	-
1	1	0	0	0	0	0	0	0	0	0	0	0	0	-
1	1	0	1	0	0	0	0	0	0	0	0	0	0	-
1	1	1	0	0	0	0	0	0	0	0	0	0	0	-
1	1	1	1	0	0	0	0	0	0	0	0	0	0	-

Значение сигнала на каждом выходе описывается формулами:

y	формула
y0	x1*x2*x3*x4
y1	***x4
y2	***
y3	***x4
y4	*x2**
y5	*x2**x4
y6	*x2**
y7	*x2*x3*x4
y8	X1***
y9	X1***x4

Пункт №2    Исследование схем последовательносной логики

А) Исследование D-триггера

В результате эксперимента нами была составлена следующая таблица переходов D-триггера:

D-вход	Предыдущее значение выходной переменной Qn	Выходное значение Qn+1
0	0	0
1	0	1
0	1	0
1	1	1

Исходя из того, что переключение элемента происходило в момент  изменения сигнала синхронизации: триггер реагировал на срез синхроимпульса то, можно сделать вывод, что исследуемый триггер является двутактным.

Б) Исследование J-K-триггера.

В ходе исследований нами было установлено, что работа JK –триггера описывается следующей таблицей:

J	K	Qn	Qn+1
0	0	0	0
0	1	0	0
1	0	0	1
1	0	1	1
0	0	1	1
0	1	1	0
1	1	0	1
1	1	1	0

Нетрудно убедиться, что режимы работы RS и JK триггеров совпадают, если вход J одного триггера  обозначить входом S  другого; и входу K  сопоставить вход R. Различие состоит в том, что для RS  триггера комбинация 1 1 на входе является запрещенной, а при подаче такой комбинации на входы JK- триггера он переходит в счетный режим—то есть инвертирует предыдущее значение выходной переменной. В этом смысле JK- триггер является более универсальным, чем  RS.

Режим работы JK триггера в режиме D-триггера можно осуществить, собрав соответствующую схему:

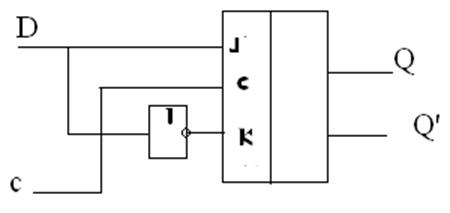В этом случае таблица состояний совпадает с таблицей, полученной в 2А. 

В) Двоично-десятичный счетчик

Временные диаграммы, полученные для двоично-десятичного счетчика:

Приложение 1.

Г) Регистр памяти.

Нами был исследован регистр памяти путем записи туда в нужной последовательности чисел от 0 до 10 с последующим их выводом на светодиодную матрицу.  Никаких неожиданных результатов получено не было.

Пункт №3 Цифро-аналоговый преобразователь.

А) Статическая характеристика преобразования ЦАП-а.

входные сигналы				соответствующее	Uвых
x1	x2	x3	x4	десятичное число
0	0	0	0	0	0
0	0	0	1	1	0,2
0	0	1	0	2	0,4
0	0	1	1	3	0,6
0	1	0	0	4	0,8
0	1	0	1	5	1
0	1	1	0	6	1,2
0	1	1	1	7	1,4
1	0	0	0	8	1,6
1	0	0	1	9	1,8

Б)Периодическая последовательность на входе двоично-десятичного  счетчика

В результате эксперимента мы получили  временные диаграммы входных (синхронизационных) и выходных импульсов.

Они составляют     Приложение 2.

Вывод: В результате исследований  нами были получены результаты полностью совпадающие с рассчитанными аналитически. Других результатов трудно было ожидать, так как  при использовании цифровых элементов вероятность ошибки(получение 0 вместо 1 и наоборот) очень мала. Наибольший интерес вызывают скачки напряжения при цифро-аналоговом преобразовании напряжения. В учебной работе они не оказывают значительного влияния на полученные результаты, однако на работу устройства, использующего данный ЦАП, такие скачки могут оказать негативное влияние.