Методы обработки экспериментальных данных

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСИЙ УНИВЕРСИТЕТ

Кафедра «Физики полупроводников и наноэлектроники»

Курсовая работа по теме:

«Методы обработки экспериментальных данных»

Преподаватель: Сидоров В. Г.

Студентка: Русина Е. А.

гр.в 4096/1

Санкт-Петербург

2011г.

Условия расчетного задания

Таблица 1. Исходные экспериментальные данные.

Функция 1		Функция 2		Функция 3
x1	y1	x2	y2	x3	y3
0	2,997	0,1	2,999	0,5	215,897
0,25	2,661	0,345	2,741	0,6	26,316
0,5	2,327	0,59	2,616	0,7	-11,274
0,75	2,055	0,835	2,544	0,8	-19,022
1	1,815	1,08	2,491	0,9	-19,647
1,25	1,584	1,325	2,439	1	-19,141
1,5	1,4	1,57	2,405	1,1	-17,715
1,75	1,23	1,815	2,372	1,2	-16,213
2	1,089	2,06	2,347	1,3	-15,084
2,25	0,941	2,305	2,314	1,4	-14,798
2,5	0,823	2,55	2,29	1,5	-13,726
2,75	0,797	2,795	2,307	1,6	-12,436
3	0,642	3,04	2,256	1,7	-11,874
3,25	0,545	3,285	2,229	1,8	-11,342
3,5	0,517	3,53	2,234	1,9	-10,501
3,75	0,434	3,775	2,208	2	-9,842
4	0,365	4,02	2,16	2,1	-9,46
4,25	0,321	4,265	2,175	2,2	-9,087
4,5	0,301	4,51	2,173	2,3	-8,847
4,75	0,266	4,755	2,162	2,4	-8,414
5	0,239	5	2,153	2,5	-8,134

1.  Найти вид и параметры функций 1 и 2.

2.  Найти параметры функции 3, заданной в виде .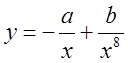

3.  Провести анализ вручную или в пакете MS Excel.

4.  Провести аппроксимацию при помощи пакета Origin.

5.  Оценить среднее квадратичное отклонение.

Расчет

            Рассмотрим функцию под номером 1. Для этого визуализируем ее графически при помощи Origin (рис. 1).

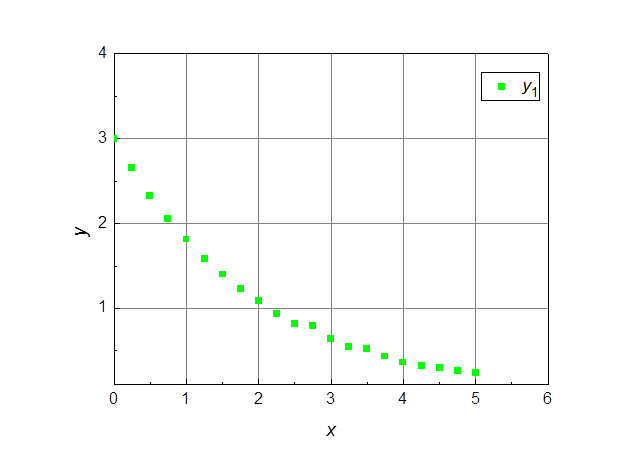
Рис. 1. Функция 1 в линейном масштабе.

            Очевидно, что данная функция принадлежит к семейству показательных функций типа . То есть данная функция должна линеаризоваться в осях (x, lg y), что мы и наблюдаем на рис. 2.

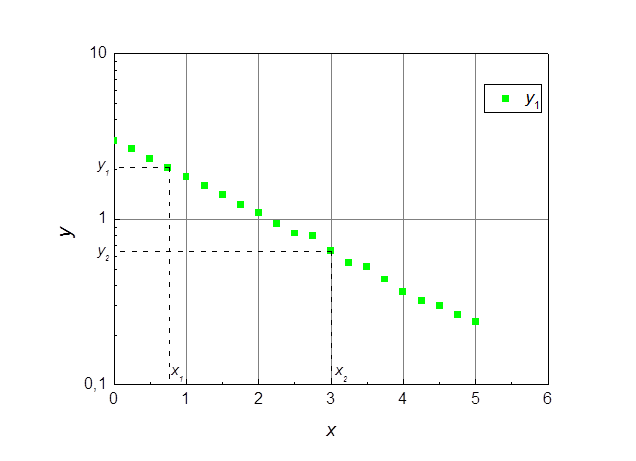
Рис. 2. Функция 1 в полулогарифмическом масштабе.

            Найдем значения параметров функции 1. В полулогарифмическом масштабе она запишется в виде: . Отсюда параметр a ‑ это значение yпри х = 0, где прямая пересекает ось ординат. А b находится из выражения 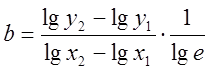. В результате расчетов получаем a = 2,997 и b = -0,517. Для проверки и анализа, нарисуем экспериментальные точки и рассчитанную кривую на одном графике (см. рис. 3). Видно, что с высокой степенью точности они совпадают.

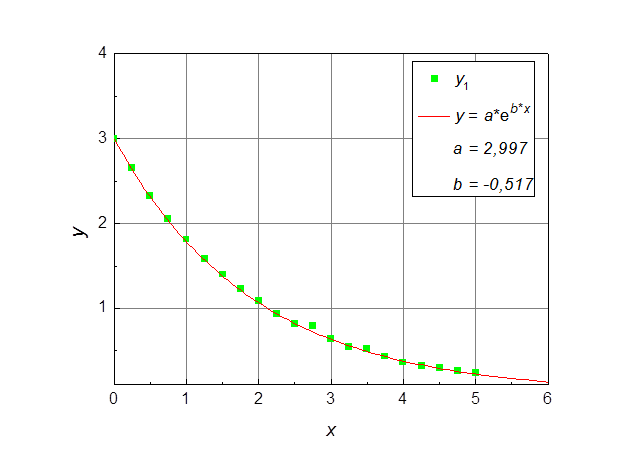
Рис. 3. Функция 1: экспериментальные точки и рассчитанная кривая.

            Теперь рассмотрим функцию номер 2. Ее графическое отображение представлено на рис. 4.

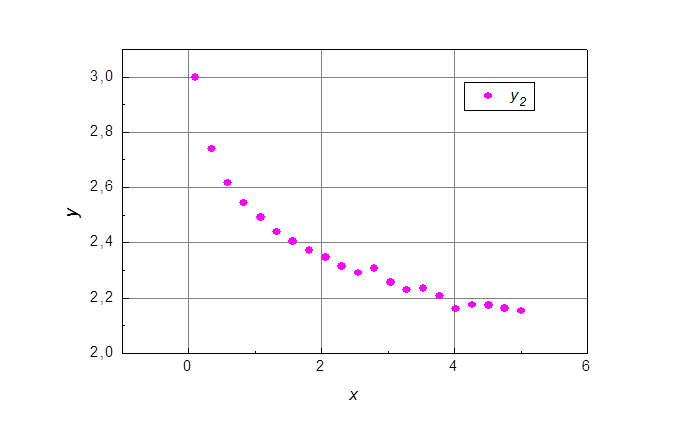
Рис. 5. Функция 2 в линейном масштабе.

            Данная функция принадлежит к семейству функций типа , где b < 0. Эти функции линеаризуются в двойном логарифмическом масштабе (см. рис. 5).

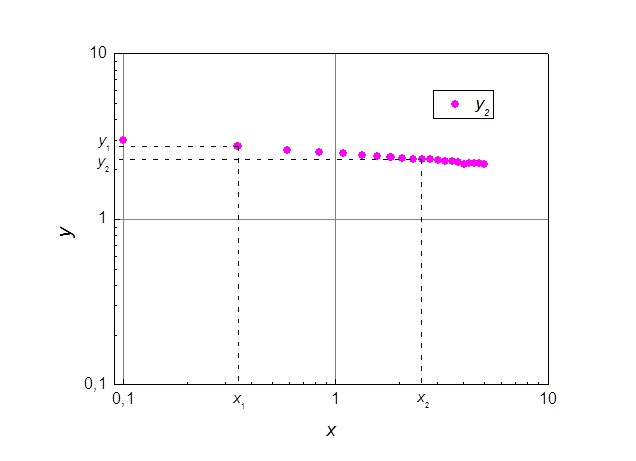
Рис. 5. Функция 2 в двойном логарифмическом масштабе.

            После логарифмирования функция 2 представляется в виде . Отсюда lg a = lg y при lg x= 0, а 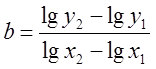. После вычислений, получаем, что a = 2,49 и b = -0,089. Для проверки построим экспериментальные точки и рассчитанную кривую на одном графике в линейном масштабе (см. рис. 6). Очевидно, что совпадают с достаточно высокой степенью точности.

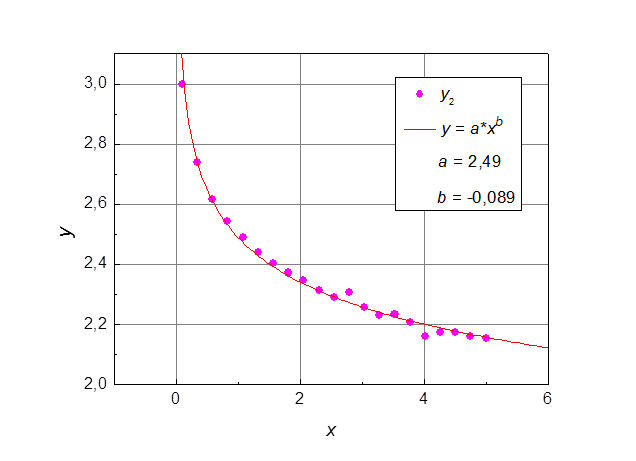
Рис. 6. Функция 2: экспериментальные точки и рассчитанная кривая.

            Далее, рассчитаем параметры функции номер 3. Ее вид нам известен ‑ 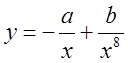. Возьмем две точки из таблицы экспериментальных данных и составим систему из двух уравнений:

.

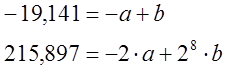            В результате решения системы получаем, что a = 20,1417 и b = 1. Для проверки результата построим сводный график рассчитанной кривой и экспериментальных данных (см. рис. 7). Видно, что экспериментальные данные достаточно хорошо описываются кривой с рассчитанными параметрами.

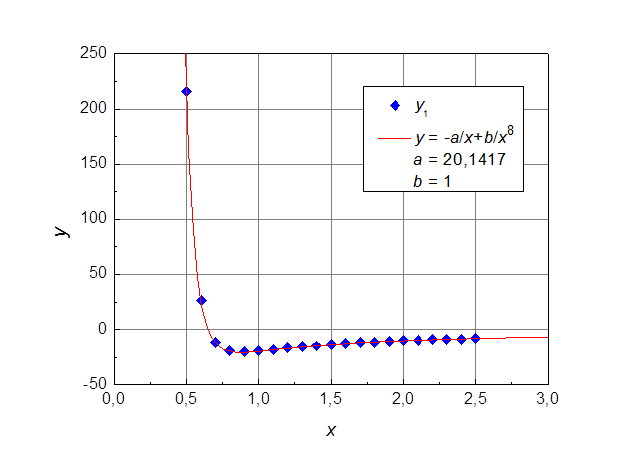
Рис. 7. Функция 3: экспериментальные точки и рассчитанная кривая.

            Теперь произведем аппроксимацию экспериментальных данных при помощи пакета Origin (рис. 8).

            Произведем расчет среднеквадратичного отклонения  по формуле для дискретных случайных величин:

                                                                       ,

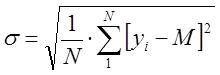где M – математическое ожидание дискретной случайной величины, N – объем выборки (N = 3). Результаты расчета представлены в таблице 2.

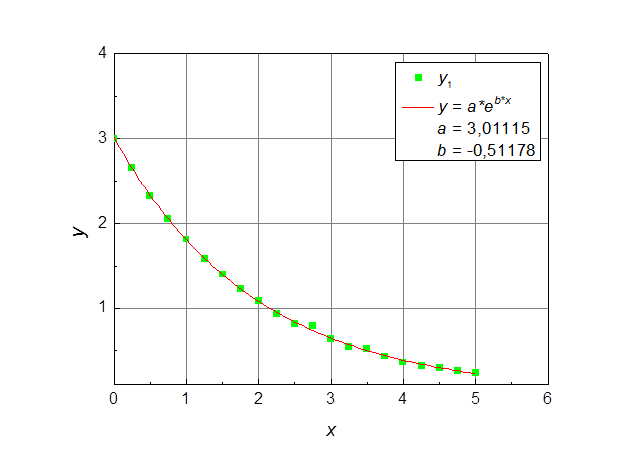
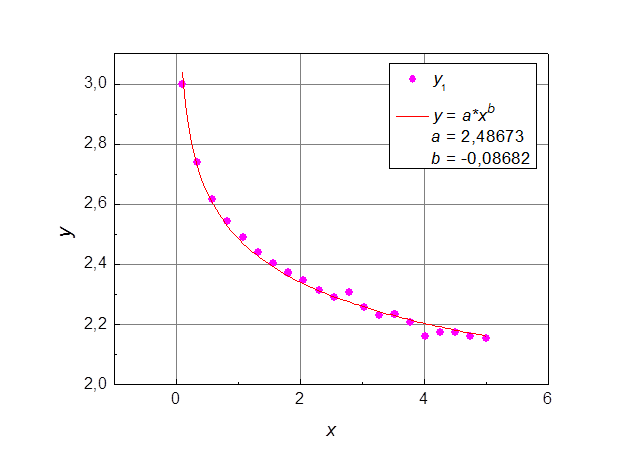
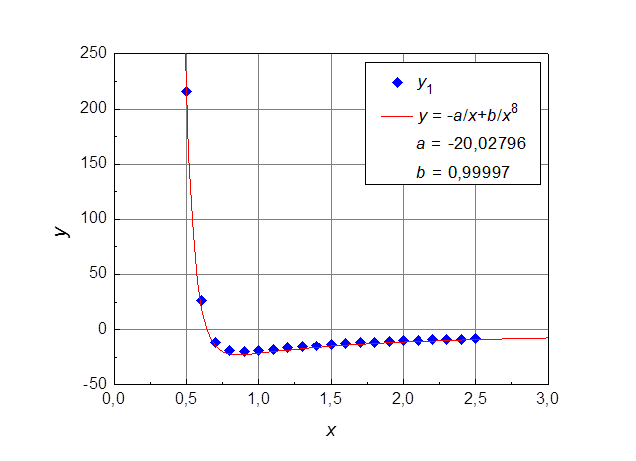
Рис. 8. Аппроксимация в Origin функциий 1 (а), 2 (б), 3(в).

Таблица 2. Сводная таблица данных.