САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра измерительных
информационных технологий
ОТЧЕТ
о лабораторной работе №8
«Измерение статических деформаций
с помощью тензорезистивных преобразователей»
Работу выполнили студенты группы 3023/1
Олейник С.
Терновая П.
Лелина А.
Глушицкий С.
Работа принята
Санкт-Петербург
2008 г.
1. Цели работы:
Практическое ознакомление
- с устройством, методами испытаний и применением тензорезисторов для измерения механических упругих деформаций механических конструкции,
- с методикой калибровки тензорезистивных преобразователей,
- с принципами построения и методами калибровки тензорезистивных измерительных преобразователей деформации и силы в напряжение и цифровой код.
2. Объекты исследования:
- тензорезисторы,
- четырехканальный тензорезистивный измерительный преобразователь деформации в напряжение,
- макет тензорезистивного измерительного преобразователя силы в напряжение.
3. Перечень оборудования и приборов:
- устройство для калибровки тензорезисторов,
- консольная балка с наклеенными на ней тензорезисторами,
- четырехканальный вторичный измерительный преобразователь изменения сопротивления тензоризосторов в напряжение,
- компьютер,
- гири.
Табл. 1. Перечень использованных средств измерений.
|
№ |
Наименование средства измерений |
Тип средства измерений |
Измеряемая величина |
Предел измерений |
Собственное сопротивление |
Предел допускаемой основной погрешности |
|
1. |
Универсальный мост Е7-10 |
ЦАП |
Сопротивление |
1мОм ¸10МОм |
> 50 МОм |
4. Программа работы:
4.1 Калибровка одиночных тензорезисторов на образцовой пластине с оценкой характеристик погрешности результатов калибровки
Задание:
Определить коэффициент тензочувствительности S тензорезистора № 6.
Расчетные формулы:
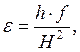
где e - относительная деформация, h – толщина пластины, Н – расстояние от точки приложения прогибающего воздействия до места закрепления пластины, ¦ - перемещение пластины.
Исходные данные:
H = 200±1 мм, h = 1±0,1мм, ¦0 = 25±1 мм, n = 6,
где n – количество повторений измерений.
Табл. 2. Экспериментальные значения сопротивления тензорезисторов.
Тензорезистор №5.
|
Перемещение винта f i , мм |
Прогиб Δ f i , мм |
Сопротивление тензорезистора, Ом |
|||||
|
f 0 |
0 |
↓ 426,06 |
↑ 427,01 |
↓ 427,01 |
↑ 428,17 |
↓ 425,75 |
↑ 425,92 |
|
f 0 + 5 |
5 |
↓ 426,32 |
↑ 427,11 |
↓ 427,28 |
↑ 428,25 |
↓ 425,80 |
↑ 426,00 |
|
f 0 + 10 |
10 |
↓ 427,10 |
↑ 427,20 |
↓ 427,52 |
↑ 428,38 |
↓ 425,94 |
↑ 426,09 |
|
f 0 + 15 |
15 |
↓ 427,21 |
↑ 427,30 |
↓ 428,46 |
↑ 428,44 |
↓ 426,20 |
↑ 426,18 |
|
f 0 + 20 |
20 |
↓ 427,31 |
↑ 427,40 |
↓ 428,52 |
↑ 428,52 |
↓ 426,32 |
↑ 426,26 |
|
f 0 + 25 |
25 |
↓ 427,43 |
↑ 427,45 |
↓ 428,61 |
↑ 428,61 |
↓ 426,36 |
↑ 426,36 |
Усредним все значения сопротивления тензористора, полученные при прогибе ¦0 и запишем это среднее значение:
R0 ср. = 426.45 Ом
Табл. 3. Обработка экспериментальных данных.
|
Прогиб Δ f i , мм |
Деформация ε i |
Относительное изменение сопротивления тензорезистора, 10-3 |
Ср. арифм. Значение 10-3 Ом |
S i 10-3 Ом |
|||||
|
0 |
0 |
-1,38 |
0,84 |
0,84 |
3,56 |
-2,11 |
-1,71 |
0,001 |
2,164 |
|
5 |
0,000125 |
-0,77 |
1,08 |
1,48 |
3,75 |
-1,99 |
-1,52 |
0,336 |
2,173 |
|
10 |
0,000250 |
1,06 |
1,29 |
2,04 |
4,06 |
-1,66 |
-1,31 |
0,910 |
2,140 |
|
15 |
0,000375 |
1,31 |
1,52 |
4,24 |
4,20 |
-1,05 |
-1,10 |
1,520 |
2,371 |
|
20 |
0,000500 |
1,55 |
1,76 |
4,38 |
4,38 |
-0,77 |
-0,91 |
1,731 |
2,340 |
|
25 |
0,000625 |
1,83 |
1,88 |
4,59 |
4,59 |
-0,68 |
-0,68 |
1,922 |
2,359 |
Вычислим для
исследованного тензорезистора:
- относительные изменения сопротивлений тензорезисторов:
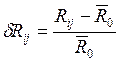 ,
,
- средние арифметические значения этих величин:
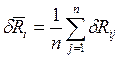 .
.
- среднеквадратические отклонения:
 .
.
Проверим статистическую гипотезу о равноточности измерений в i-х точках по критерию Кочрена. Для этого вычислим значение этого критерия:
![]()
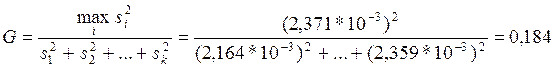
и сравним его с критическим значением критерия Кочрена. Видим, что
g(a = 0,05; k
= 6; n = 6) = 0.04447 т.е. g >
G. Следовательно, гипотеза о
равноточности измерений не отклонена. Тогда коэффициент тензочувствительности ![]() и среднеквадратическое значение VS случайной составляющей погрешности
можно вычислить по формулам:
и среднеквадратическое значение VS случайной составляющей погрешности
можно вычислить по формулам:
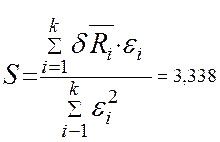
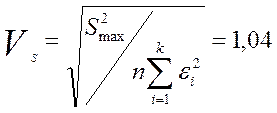
Так как калибровка производилась для одного тензорезистора, то говорить о метрологических характеристиках партии тензорезисторов не имеет смысла.
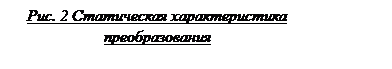 |
Вычислим предельное значение относительной систематической погрешности воспроизведения деформаций:
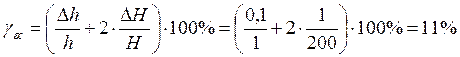
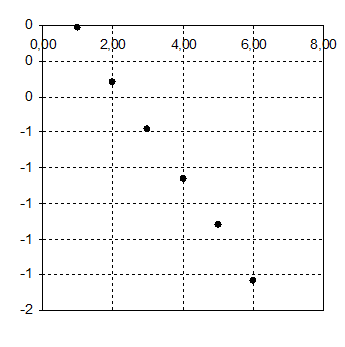
Поскольку зависимость между относительной деформацией и относительным изменением сопротивления тензорезистора теоретически линейна,
![]()
Границы интервала ![]() для случайной составляющей абсолютной
погрешности определения коэффициента S определим с помощью коэффициента Стьюдента:
для случайной составляющей абсолютной
погрешности определения коэффициента S определим с помощью коэффициента Стьюдента:
![]()
Значение коэффициента Стьюдента (Q = 0,95; n = 6) равно 2,57. Следовательно,
Границы интервала неопределенности значения
систематической составляющей абсолютной погрешности ![]() вычислим
по формуле:
вычислим
по формуле:
Границы интервала ![]() ,
содержащего с вероятностью Р (мы примем Р = 0,95) значения общей погрешности
определения коэффициента тензочувствительности одного тензорезистора,
определяются суммой:
,
содержащего с вероятностью Р (мы примем Р = 0,95) значения общей погрешности
определения коэффициента тензочувствительности одного тензорезистора,
определяются суммой:
И это значение ![]() принимается в
качестве характеристики погрешности коэффициента тензочувствительности
отдельного r-го тензорезистора, подвергнутого
испытаниям.
принимается в
качестве характеристики погрешности коэффициента тензочувствительности
отдельного r-го тензорезистора, подвергнутого
испытаниям.
Вывод:
В соответствии с заданием, мы определили коэффициент тензочувствительности тензорезистора №6 и вычислили значение границ интервала, содержащего с вероятностью Р = 0,95 значения общей погрешности определения коэффициента тензочувствительности одиночного тензорезистора:
4.2 Калибровка макета тензорезистивного преобразователя силы в напряжение.
Задание:
Провести калибровку канала № 1 макета тензорезистивного преобразователя силы в напряжение.
Исходные данные:
n = 11, где n – количество повторений измерений.
Табл. 4. Экспериментальные значения средних арифметических значений и дисперсии напряжения.
|
Р, Н |
|
si, В |
|
0 |
0,005152 |
0,000267 |
|
5 |
1,290606 |
0,000136 |
|
10 |
2,541515 |
0,000082 |
|
15 |
3,837875 |
0,000076 |
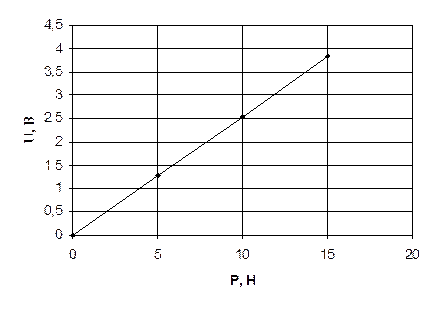
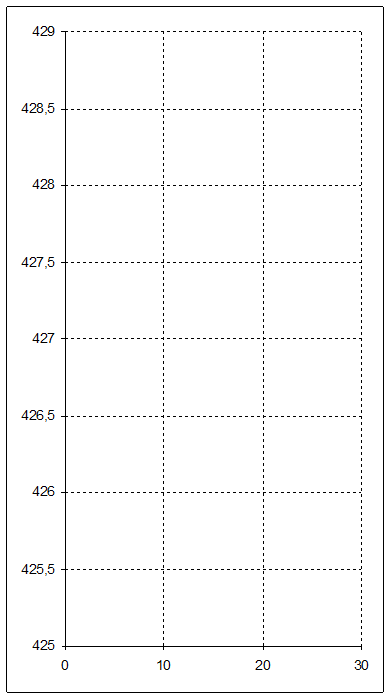
Рис. 3. График линейной характеристики преобразования силы в напряжение.
Проверим статистическую гипотезу о равноточности измерений в i-х точках по критерию Кочрена. Для этого вычислим значение этого критерия:
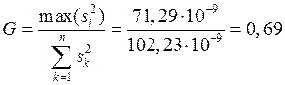
и сравним его с критическим значением критерия Кочрена. Видим, что
g(a = 0,05; k = 4; n = 11) = 0,4899
т.е. g < G. Следовательно, гипотеза о равноточности измерений отклонена. Тогда коэффициент линейной зависимости КР и среднеквадратическое значение SК случайной составляющей погрешности можно вычислить по формулам:
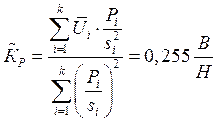
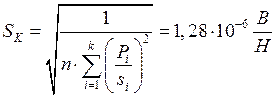
Оценим характеристики аддитивной и мультипликативной составляющих погрешности макета преобразователя силы.
В нашем случае мультипликативная погрешность содержит систематическую составляющую, порожденную систематической погрешностью гирь. Поэтому ширина интервала неопределенности случайной составляющей мультипликативной погрешности преобразователя должна быть увеличена на ширину интервала неопределенности систематической составляющей.
Границы интервала ![]() для
случайной составляющей абсолютной погрешности коэффициента преобразования:
для
случайной составляющей абсолютной погрешности коэффициента преобразования:
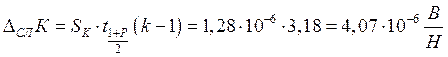 ,
,
где ![]() = 3,18 –
коэффициент Стьюдента
= 3,18 –
коэффициент Стьюдента
Границы интервала неопределенности значения
систематической составляющей абсолютной погрешности ![]() вычисляются
по формуле:
вычисляются
по формуле:
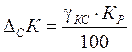 ,
,
где по тем же причинам, что и в п. 4.1, предельное значение
![]() относительной систематической
погрешности определения коэффициента К равно предельному значению
систематической погрешности гирь, т.е. 2%. Следовательно,
относительной систематической
погрешности определения коэффициента К равно предельному значению
систематической погрешности гирь, т.е. 2%. Следовательно,
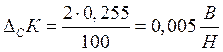
Границы интервала ![]() ,
содержащего с вероятностью Р = 0,95 значение общей погрешности определения
коэффициента преобразования, определяются суммой:
,
содержащего с вероятностью Р = 0,95 значение общей погрешности определения
коэффициента преобразования, определяются суммой:
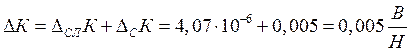
Определим коэффициент с двучленной формулы:
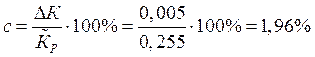
Определим предельное значение абсолютной аддитивной погрешности:
![]()
Теперь определим коэффициент d двучленной формулы:
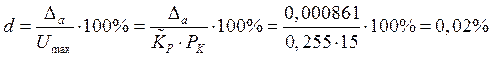
 Полученная
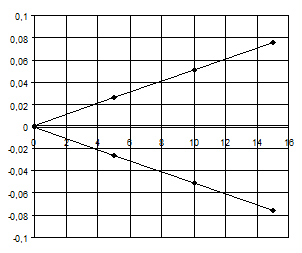
формула для предельных относительных погрешностей преобразователя силы можно
представить на графике, как область, ограниченную двумя прямыми:
Полученная
формула для предельных относительных погрешностей преобразователя силы можно
представить на графике, как область, ограниченную двумя прямыми:
![]()
![]()
Рис. 4. Графическое представление мультипликативной
и аддитивной погрешностей преобразования.
Вывод:
В ходе работы мы ознакомились с методикой калибровки тензорезистивных преобразователей, с принципами построения и методами калибровки тензорезистивных измерительных преобразователей деформации и силы в напряжение и цифровой код. Мы вычислили среднеарифметические и среднеквадратические значения напряжений в i-ых точках, проверили гипотезу о равноточности измерений и вычислили значения , коэффициенты двучленной формулы с и , нормирующей относительную погрешность преобразователя, построили график линейной характеристики преобразования с представлением границ разброса экспериментальных данных и графически представили аддитивную и мультипликативную погрешности преобразователя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.