Построение графика статистической функции распределения. Построение гистограммы наработок между отказами

1. Исходные данные:

Наработка до отказа имеет распределение приведенное в таблице 1. Определить 80% ресурс машины с использованием вероятностных сеток.

Таблица 1 – Наработка до отказа, ч.

2021	509	841	2342	509	633	538	1237	928	286
776	1872	658	980	786	724	651	7302	903	1288
628	901	736	861	1345	1611	264	725	3744	1146
735	1665	559	1368	1705	619	1160	1199	379	667

2. Построение графика статистической функции распределения

Удобным способом получить представление о распределении случайной величины Х является построение графика статистической функции распределения выборки (х₁, … х_n).

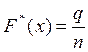,                                                                                                                  (1)

где q – число опытов, в которых случайная величина Х принимала значения меньше х; n – общее число произведенных опытов.

Статистический ряд перестраивается так, чтобы полученные числовые значения случайной величины располагались в возрастающем порядке (вариационный ряд).

Для возрастающего ряда эмпирическая функция распределения записывается:

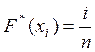 ,                                                   (2)

где i – порядковый номер опыта.

Таблица 2 – Вариационный ряд

i*	1	2	3	4	5	6	7	8	9	10
li	264	286	379	509	509	538	559	619	628	633
i/n	0,025	0,05	0,075	0,1	0,125	0,15	0,175	0,2	0,225	0,25

11	12	13	14	15	16	17	18	19	20
651	658	667	724	725	735	736	776	786	841
0,275	0,3	0,325	0,35	0,375	0,4	0,425	0,45	0,475	0,5

21	22	23	24	25	26	27	28	29	30
861	901	903	928	980	1146	1160	1199	1237	1288
0,525	0,55	0,575	0,6	0,625	0,65	0,675	0,7	0,725	0,75

31	32	33	34	35	36	37	38	39	40
1345	1368	1611	1665	1705	1875	2021	2342	3744	7302
0,775	0,8	0,825	0,85	0,875	0,9	0,925	0,95	0,975	1

3. Построение гистограммы наработок между отказами.

Из данных статистического ряда для непрерывных величин строится гистограмма, изображающая статистическую плотность распределения:

Плотность распределения:

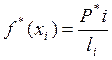;                                                                                                                (3)

где P^*i – частость; l_i – длина разряда.

Частость:

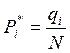,                                                                                                                (4)

где q_i – число наблюдений в разряде (частота).

Длина разряда:

,                                                                                                                (5)

где  - максимальное значение случайной величины в разряде i;

 -  минимальное значение случайной величины в разряде i.

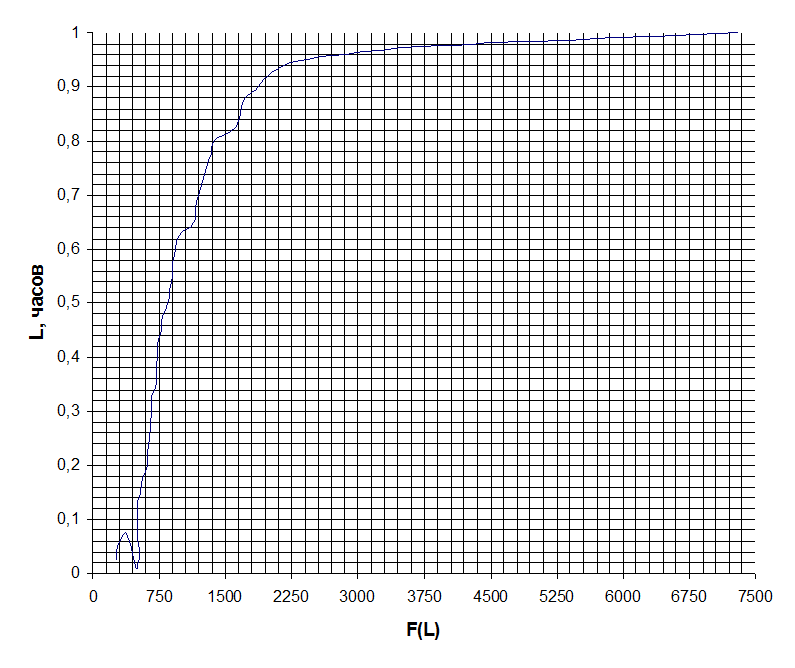Рисунок 1 – График функции распределения.

Гистограмма построена на ЭВМ при помощи программы STATISTICA 6.0

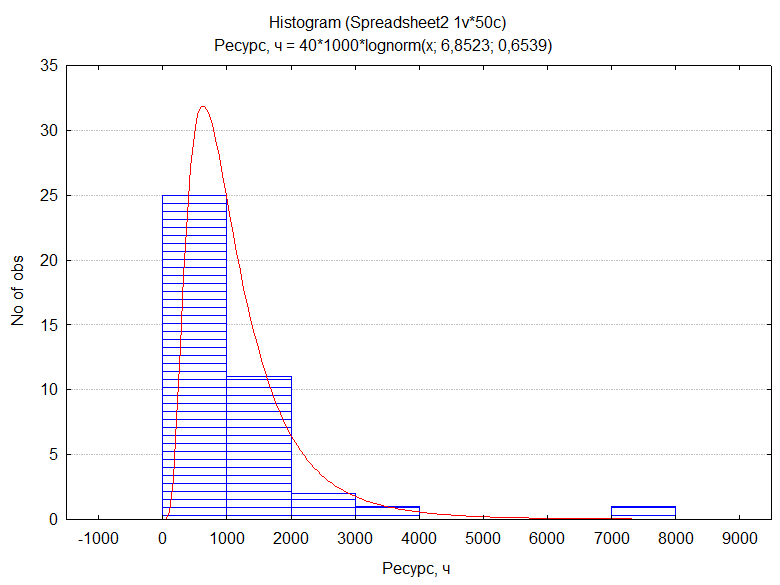
Рисунок 2 – Гистограмма наработок между отказами.

На гистограмму путем подбора наложена кривая логорифмически нормального закона распределения, которая наиболее подходит к данной гистограмме.

3. Построение графика функции распределения на вероятностной сетке.

При небольшом числе опытов для определения закона распределения, его параметров, значений гамма-процентного ресурса и вероятности безотказной работы удобно пользоваться вероятностными шкалами. На сетке, построенной на этих шкалах, график функции распределения является прямой линией.

Расстояние до точки  z от начала координат (мм):

,                                                                                                                     (6)

где K_z– масштабный фактор.

Для нормального и экспоненциального законов распределения, где шкала по оси t равномерная, масштабный фактор K_tопределяется в зависимости от области изменения величины t:

                                                                                                                       (7)

Если за ширину графика принять величину L (мм), то значения t на горизонтальной оси следует откладывать при помощи соотношения:

,                                                                                                                     (8)

где масштабный фактор  K_t:

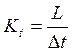,                                                                                                                     (9)

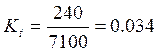
4. Нормальное распределение

Квантиль при нормальном распределении вычисляем по формуле:

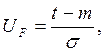                                                                                                                                      (13)

где m,  - параметры распределения.

При построении шкалы F(t) наименьшее и наибольшее значения функции распределения принимаются равными 0,001 и 0,999. Тогда для U_F наименьшее значение будет –3,09 и наибольшее 3,09.

Уравнение для S_F при длине шкалы 150 мм определяем по:

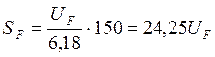                                                                                                                                      (14)

Горизонтальная шкала равномерная. Масштабный фактор K_t находим по (9).

Среднее квадратичное отклонение:

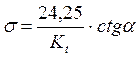                                                                                                                                      (15)

где - угол, образованный прямой с осью t.

График функции нормального распределения изображен на рисунке 3.

Масштабный фактор K_t = 0,034 (был определен в п.3)

5. Логарифмически нормальное распределение.

Для логарифмически нормального распределения величина S_F по той же формуле (14):

Горизонтальная шкала t неравномерная, логарифмическая.

Величина S_t определяется по формуле:

S_t = 100lgt,                                                                                                      (16)

в которой значения изменяются в пределах от 1 до 10, от 10 до 100, от 100 до 1000, от 1000 до 10000 и т.д. Длина шкалы при этом составляет 100 мм.

Для диапазона изменения оси от 10 до 100 рассматривается величина 10t.

Тогда:

S_10t = 100lg10t=100+S                                                                                                                                                                                                                                (17)

Для диапазона изменения t от 100 до 1000 получим:

S_100t = 200 + S_t                                                                                                                                       (18)

Математическое ожидание определяется также как и для нормального распределения.

Среднее квадратическое отклонение:

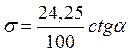.                                                                                                                                     (19)

Для построения графика логарифмически нормального распределения необходимо определить масштабный фактор K_t. Горизонтальная шкала графика равна 240 мм и будет состоять из 2 диапазонов изменения: от 100 до 1000 и от 1000 до 10000.

Ширина графика определяется по формуле:

L = I – II –  III,                                                                                                                                 (20)

где I – длина участка 100 – 1000 (мм)

II – длина участка 1000 – 10000 (мм)

Длины I, II, показаны на рисунке

Длину участка I определяем по формуле (16):

I = 200+100 lg1000= 500 мм                               

Длина участка II определяется аналогично I:

II = 100 lg7,302 = 8,8 мм

Значит ширина графика по (20) равна:

L = 85,5 – 8,8 – 14,5 = 63,2 мм

Масштабный фактор определяем по формуле (9):

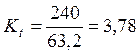
Далее, учитывая масштабный фактор и используя формулу (8) строим рисунок