Лабораторная работа № 3.
«Сетевой график»
Сетевое планирование и управление – один из методов графо-аналитического планирования и управления большим комплексом взаимосвязанных работ с большим количеством участников и исполнителей.
Основой метода является графическая модель – сетевой график. Его элементами являются:
работа – процесс, требующий затрат времени и ресурсов
![]()
событие - факт окончания одной или нескольких работ, необходимых для начала последующих работ
![]()
ожидание – процесс, требующий затрат времени
![]()
зависимость (фиктивная работа)- не требует ни затрат времени, ни ресурсов, а используется для логической взаимосвязи между работами
![]()
По роли в сетевом графике, события бывают:
· исходное (начальное)
· завершающее (конечное)
· промежуточное
События нумеруются, у события есть параметры:
tр – ранний срок совершения события;
tп – поздний срок совершения события,
Ri – резерв.
Исходные данные Таблица 1
|
Код работ |
Продолжит. |
Кол-во раб. |
Раннее нач. |
Раннее оконч. |
Позднее нач. |
Позднее оконч. |
Полн. резерв |
Своб. резерв |
|
0-1 |
3 |
5 |
0 |
3 |
3 |
6 |
3 |
0 |
|
0-2 |
7 |
4 |
0 |
7 |
4 |
11 |
4 |
1 |
|
0-3 |
6 |
2 |
0 |
6 |
0 |
6 |
0 |
0 |
|
1-2 |
5 |
3 |
3 |
8 |
6 |
11 |
3 |
0 |
|
1-3 |
||||||||
|
1-4 |
6 |
5 |
3 |
9 |
6 |
12 |
3 |
0 |
|
1-6 |
5 |
3 |
3 |
8 |
10 |
15 |
7 |
4 |
|
2-6 |
4 |
4 |
8 |
12 |
11 |
15 |
3 |
0 |
|
2-8 |
10 |
2 |
8 |
18 |
17 |
27 |
9 |
9 |
|
3-5 |
9 |
3 |
6 |
15 |
6 |
15 |
0 |
0 |
|
4-5 |
3 |
2 |
9 |
12 |
12 |
15 |
3 |
3 |
|
4-6 |
||||||||
|
5-7 |
6 |
1 |
15 |
21 |
15 |
21 |
0 |
0 |
|
6-7 |
6 |
4 |
12 |
18 |
15 |
21 |
3 |
3 |
|
6-8 |
6 |
4 |
12 |
18 |
21 |
27 |
9 |
9 |
|
7-8 |
6 |
2 |
21 |
27 |
21 |
27 |
0 |
0 |
|
8-9 |
4 |
6 |
27 |
31 |
27 |
31 |
0 |
0 |
Алгоритм СПУ:
1) Определяют состав комплекса работ, их взаимосвязи и последовательности выполнения;
2) Строится сетевой график и нумеруются события;
3) На основе принятого метода оценок определяется время выполнения каждой работы;
4) Рассчитываются параметры сетевого графика;
5) Проводится анализ графика по времени и трудовым ресурсам с учётом ограничений;
6) Проводится оптимизация. Строится линейный график и график движения рабочей силы;
7) Оптимизация сетевого графика и его пересчёт с новыми параметрами.
Состав комплекса работ
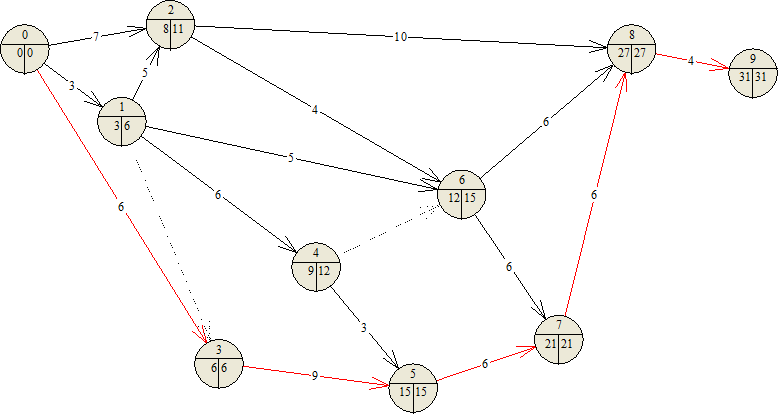
Максимальная продолжительность работ: 31 – наиболее ранние сроки совершения работ.
Расчёт параметров работ
Проводим анализ и построим 2 графика:
линейный график (график Ганта) и график рабочей силы.
Ri-j=tп-tр-ti-j ri-j=tjр-tiр-ti-j
Ri-j< ri-j
График движения рабочей силы – изменение количества одновременно занятых работников по времени.
Трудоёмкость=Человек/Часы
Находим tiп=[tjп-ti-j]min. Если событие критическое, то tiп=tjп, расчёт ведется справа налево, если несколько работ, берётся min. Резерв возникает только в сложных событиях.
После построения графика ведётся анализ по времени и ресурсам, т. е. численность расчётная сопоставляется заданной и продолжительность критическая с заданной.
Φрасчётная>Φрасполагаемая
Ткритическая>Тдир – необходима оптимизация.
Неоптимизированный график
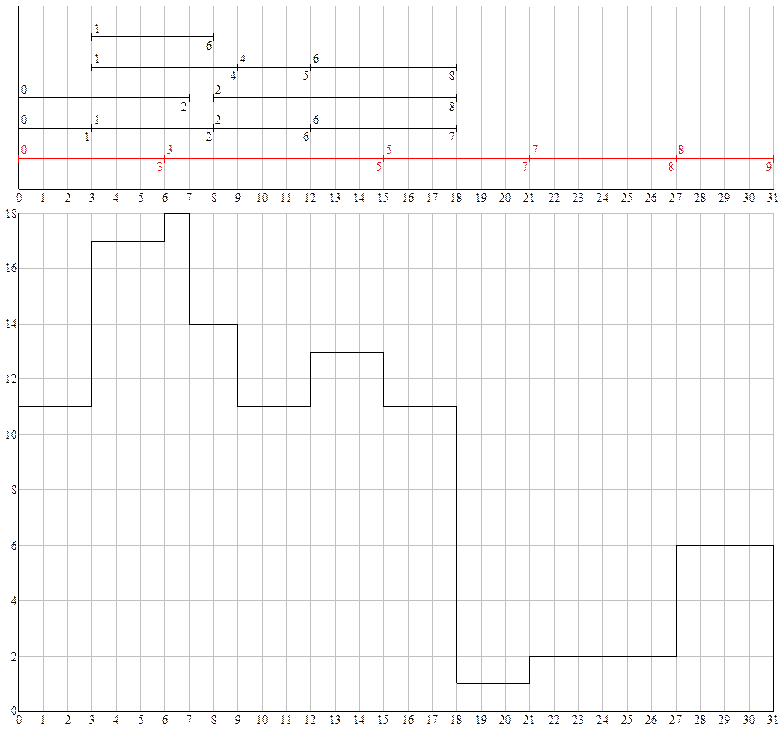
Оптимизация – приведение расчетных данных в соответствии с ограничениями задания.
Пути оптимизации:
1. Использование свободных резервов работ с целью передачи людей на работы критического пути (использование резервов не ограничивает работы, предшествующие и последующие в резервах). При этом трудоёмкость работ не меняется.
2. Использование полных резервов. Использование Ri-j лишает все последующие работы резервов.
3. Изменение топологии сети (последовательность и параллельность цепи).
В данном задании необходимо привести графики к критическим значениям численности человек – 13 и продолжительности трудового периода – 29 дней.
Оптимизированный график (по численности)
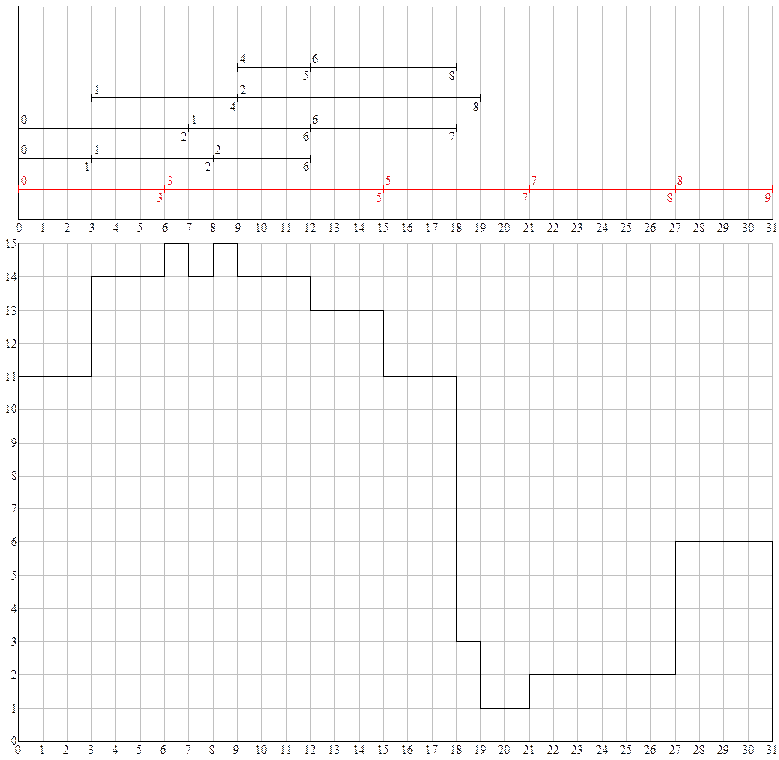
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.