


























Энергетический метод представляет собой универсальный способ определения перемещений упругих систем. Он основан на применении закона сохранения энергии и принципа возможных перемещений.
К упругим системам относятся балки, рамы, фермы и т.п., которые соответствуют следующим условиям:
- линейно-деформируемые системы (материал подчиняется закону Гука);
- материал идеально упругий;
- наибольшие напряжения в системах не
превышают предела пропорциональности ![]() ;
;
- применимость принципа начальных размеров;
- применимость принципа независимости действия сил (ПНДС).
Будем рассматривать только статическое нагружение упругих систем, при котором нагрузка возрастает постепенно и таким образом, что ускорениями элементов системы можно пренебречь.
При нагружении деформируемых систем имеет место преобразование потенциальной энергии одного вида в другой.
Обозначим
величину накопленной потенциальной энергии деформации через U, а потенциальную энергию внешних
нагрузок через ![]() . Закон сохранения
потенциальной энергии имеет вид
. Закон сохранения
потенциальной энергии имеет вид
![]()
![]() (2.1)
(2.1)
Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию. Тогда величина UF измеряется положительной работой этих нагрузок. Накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних сил упругого сопротивления (если учесть их направление по отношению к деформации, вызванной внешними силами).
Заменив в формуле
(2.1) величины U и ![]() численно
равными им значениями работ
численно
равными им значениями работ ![]() и
и ![]() , получим иную формулировку этого
закона
, получим иную формулировку этого
закона ![]() , или
, или
![]() . (2.2)
. (2.2)
Из равенства (2.2) следует, что при перемещениях точек системы без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю.
Каждому виду нагрузки соответствует свое перемещение, на котором она производит работу. Сосредоточенной силе соответствует линейное перемещение, сосредоточенному моменту – угловое перемещение. Чтобы наши рассуждения и выводы носили общий характер, введем понятие обобщенной силы.
Под обобщенной силой F понимается любое силовое воздействие. Перемещение Δ, на котором она совершает работу, называют обобщенным перемещением.
Условимся
обобщенные перемещения (как линейные, так и угловые) обозначать символом Δ с
двумя индексами – ![]() :
:
· первый (буква или номер) определяет точку или направление перемещения;
· второй – причину, вызвавшую его.
Для обозначения
полного перемещения, вызванного несколькими усилиями, при знаке ![]() сохраняется только первый индекс.
Например, перемещение
сохраняется только первый индекс.
Например, перемещение ![]() точки приложения силы F по направлению ее линии действия
(рис. 2.1), вызванное этой же силой
точки приложения силы F по направлению ее линии действия
(рис. 2.1), вызванное этой же силой ![]() , силой
, силой ![]() и парой сил
и парой сил ![]() , запишется в виде суммы этих перемещений
, запишется в виде суммы этих перемещений
![]()
![]()
![]() Перемещение, вызванное единичной
силой
Перемещение, вызванное единичной
силой ![]() или единичным моментом
или единичным моментом ![]() будем обозначать символом
будем обозначать символом ![]() При обозначении единичных нагрузок
принято вводить черту над соответствующей буквой. Единичные нагрузки считаются
безразмерными величинами.
При обозначении единичных нагрузок
принято вводить черту над соответствующей буквой. Единичные нагрузки считаются
безразмерными величинами.
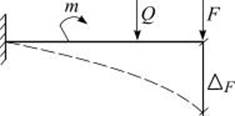
Рис. 2.1
Если единичная
сила ![]() (рис. 2.2 а) вызвала перемещение
(рис. 2.2 а) вызвала перемещение ![]() , то на основании принципа
независимости действия сил полное перемещение, вызванное силой F(рис. 2.2 б), равно
, то на основании принципа
независимости действия сил полное перемещение, вызванное силой F(рис. 2.2 б), равно
![]() . (2.3)
. (2.3)
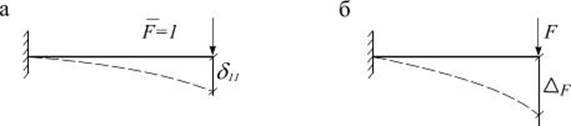
Рис. 2.2
Если нагрузка
обозначается с числовыми индексами, то буквенные индексы при ![]() и
и ![]() заменяются
соответствующими числами (
заменяются
соответствующими числами (![]() ).
).
2.2.1. Работа внешних сил
Перемещение сечения по направлению действия силы, вызванное самой силой, называется действительным перемещением.
Вычислим работу
обобщенной силы F, статически возрастающей до
своего конечного значения (рис. 2.3 а), на действительном перемещении ![]() . График зависимости между силой F и перемещением
. График зависимости между силой F и перемещением ![]() представляет
собой наклонную прямую (рис. 2.3 б).
представляет
собой наклонную прямую (рис. 2.3 б).
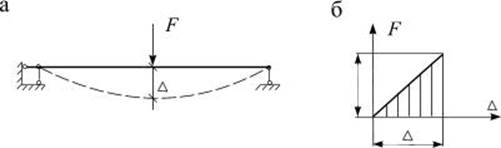
Рис. 2.3
![]() Работа силы F численно равна площади заштрихованного треугольника, см. рис. 2.3 б:
Работа силы F численно равна площади заштрихованного треугольника, см. рис. 2.3 б:
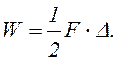 (2.4)
(2.4)
Таким образом, действительная работа при статическом действии обобщенной силы на упругую систему равна половине произведения конечного значения силы на конечное значение обобщенного перемещения по ее направлению (теорема Клайперона).
Работа совокупности статически приложенных сил вычисляется по формуле
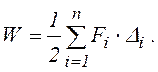 (2.5)
(2.5)
2.2.2. Работа внутренних сил на действительных перемещениях
Двумя смежными сечениями выделим из стержня элемент длиной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.