


















Если одно из главных напряжений равно нулю, то напряженное состояние (н.с.) называется плоским (двухосным) (рис. 9.2 б). Если равны нулю два главных напряжения, то напряженное состояние называется линейным (одноосным) (рис. 9.2 в).
Линейное н.с. имеет место в стержнях, работающих на растяжение или сжатие, в некоторых точках стержня, работающего на изгиб или сложное сопротивление.
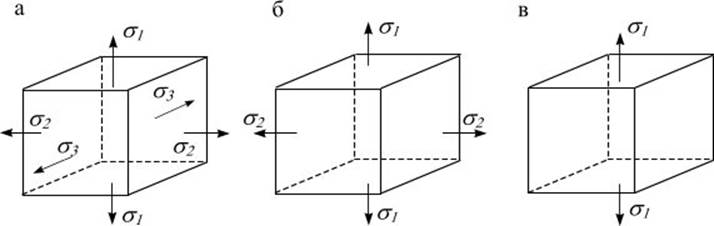
Рис. 9.2
Плоское н.с. имеет место при кручении, сдвиге, изгибе и сложном сопротивлении бруса. В условиях плоского н.с. работают элементы в виде пластин и оболочек (панели, перегородки, стенки и днища резервуаров, листовые конструкции).
Объемное н.с. возникает в материале дорожного покрытия в месте давления колеса на плиту покрытия, в месте контакта колеса с поверхностью рельса, аналогично в грунтовом массиве.
9.2. Линейное напряженное состояние
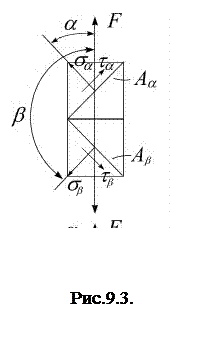
Линейное напряженное состояние реализуется при растяжении (сжатии) стержней (рис. 9.3). Напряжения в поперечном сечении
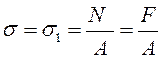 .
(9.1)
.
(9.1)
|
||||
 |
||||
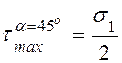
Главные напряжения:
![]()
9.3. Плоское напряженное состояние
При плоском напряженном состоянии на площадке ![]() действуют нормальные и касательные
напряжения (рис. 9.4).
действуют нормальные и касательные
напряжения (рис. 9.4).
Применяя принцип суперпозиции, на основании (9.2) и (9.3) имеем:
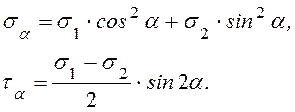 (9.4)
(9.4)
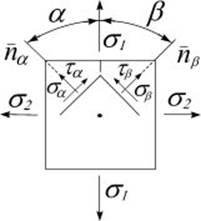
Рис. 9.4
Напряжения на площадке ![]() ,
перпендикулярной площадке
,
перпендикулярной площадке ![]() , с учетом
(9.4), будут определяться:
, с учетом
(9.4), будут определяться:
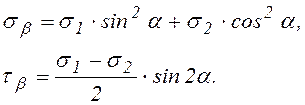 (9.5)
(9.5)
Из данных формул следует:
1. что касательные напряжения достигают максимальных
значений при ![]() и равны:
и равны:
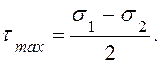 (9.6)
(9.6)
2.Складывая выражения для нормальных напряжений (формулы 9.4 и 9.5), получим:
![]() , т.е. сумма
нормальных напряжений на взаимно перпендикулярных площадках постоянна и равна
сумме главных напряжений.
, т.е. сумма
нормальных напряжений на взаимно перпендикулярных площадках постоянна и равна
сумме главных напряжений.
3. Сопоставляя (9.4) и (9.5), получим ![]() –
закон парности касательных напряжений.
–
закон парности касательных напряжений.
При известных нормальных и касательных напряжениях по
площадкам ![]() и
и ![]() могут
быть установлены главные напряжения
могут
быть установлены главные напряжения ![]() и
и
![]() , имеющие экстремальную
(наибольшую и наименьшую) величину:
, имеющие экстремальную
(наибольшую и наименьшую) величину:
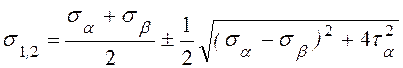 (9.7)
(9.7)
и направления главных напряжений
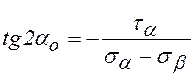 .
(9.8)
.
(9.8)
Приведенные формулы связывают главные напряжения и напряжения по наклонным площадкам.
В теории напряженного состояния различают две основные задачи:
Прямая – по известным главным площадкам и
действующим на них главным напряжениям требуется определить нормальные и
касательные напряжения на наклонных площадках под углом ![]() ;
;
Обратная – по известным нормальным и касательным напряжениям, действующим на двух взаимно перпендикулярных площадках, найти главные напряжения и главные направления.
9.4. Прямая задача при плоском напряженном состоянии. Круг Мора
Аналитическое решение прямой задачи дается формулами (9.4).
Графически ![]() ,
, ![]() ,
, ![]() ,
,
![]() по известным
по известным ![]() ,
, ![]() (рис.
9.5 а) определяются с помощью круга Мора (рис. 9.5 б).
(рис.
9.5 а) определяются с помощью круга Мора (рис. 9.5 б).
Круг Мора (круг напряжений) – геометрическое место точек, абсциссы и ординаты которых равны соответственно нормальным и касательным напряжениям, возникающим на площадках данной серии.
|
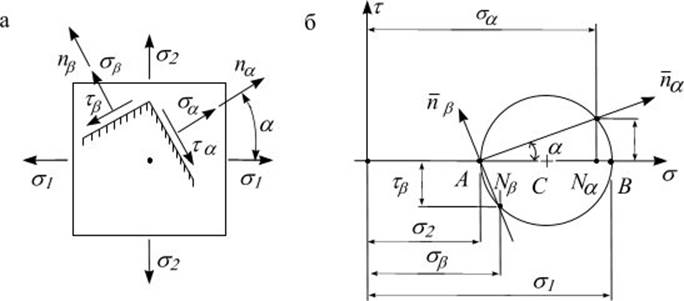
Рис. 9.5
Серией площадок называют совокупность бесчисленного множества площадок, перпендикулярных одной и той же грани элементарного параллелепипеда.
1. На плоскости выбирается ось ![]() (ось абсцисс) параллельно 1–му
главному напряжению.
(ось абсцисс) параллельно 1–му
главному напряжению.
2. Выбирается ось ординат – ось
касательных напряжений ![]() .
.
3. На оси абсцисс откладываются
главные напряжения ![]() ,
, ![]() (с
учетом их знаков), и на разности этих напряжений, как на диаметре, строится
круг напряжений (круг Мора). Точка В характеризует напряжения по вертикальным
боковым граням параллелепипеда, изображенного на рис. 9.5,а, а точка А –
по его горизонтальным граням.
(с
учетом их знаков), и на разности этих напряжений, как на диаметре, строится
круг напряжений (круг Мора). Точка В характеризует напряжения по вертикальным
боковым граням параллелепипеда, изображенного на рис. 9.5,а, а точка А –
по его горизонтальным граням.
4. Из точек В и А
проводятся лучи параллельные нормалям к соответствующим граням, до пересечения
с окружностью в точке К, называемой полюсом. Затем из точки К
проводится луч, параллельный нормали ![]() ; точка
пересечения луча с кругом
; точка
пересечения луча с кругом ![]() определяет
напряжения
определяет
напряжения ![]() на площадке
на площадке ![]() .
.
5. Из этой же точки проводится луч, параллельный нормали nβ, пересечение которого с кругом Мβ дает σβ и τβ (рис.9.5 б). Из построений можно получить формулы 9.4:
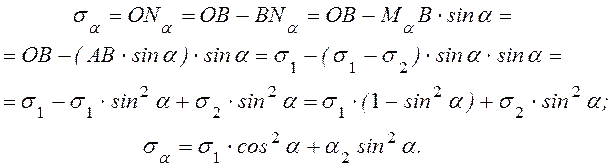
Аналогично
для ![]() :
: ![]() .
.
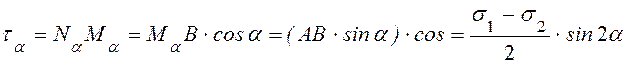 .
.
9.5. Обратная задача. Определение главных напряжений с помощью
круга Мора
Известно ![]() ,
, ![]() ,
, ![]() ,
,
![]() (рис. 9.6 а). Пусть
(рис. 9.6 а). Пусть ![]() . Определить
. Определить ![]() ,
, ![]() .
.
1. Ось абсцисс параллельна
большему из напряжений ![]() (рис. 9.6 б).
(рис. 9.6 б).
2. Ось касательных напряжений перпендикулярна оси нормальных напряжений.
3. На оси абсцисс откладываются ![]() ,
,
![]() (точки
(точки ![]() и
и
![]() ).
).
4. Из концов ![]() и
и ![]() откладываются отрезки
откладываются отрезки ![]() и
и ![]() (точки
(точки
![]() и
и ![]() ),
концы
),
концы ![]() и
и ![]() соединяются.
соединяются.
|
|
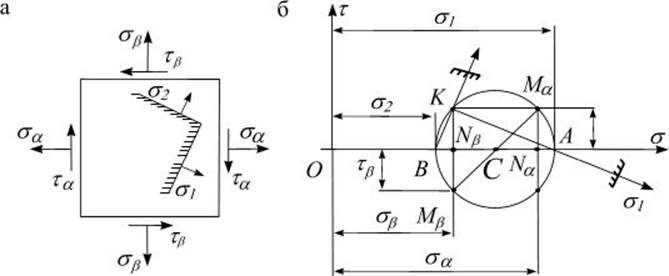
Рис. 9.6
5. На линии, соединяющей концы ![]() и
и
![]() , как на диаметре, строится круг
Мора, который отсекает на оси абсцисс отрезки ОА и ОВ, равные
, как на диаметре, строится круг
Мора, который отсекает на оси абсцисс отрезки ОА и ОВ, равные ![]() и
и ![]() .
.
6. Из точек ![]() и
и ![]() проводят
лучи параллельные нормалям к вертикальной и горизонтальной граням параллепипеда
до пересечения с окружностью в точке К (полюс круга). Направления
проводят
лучи параллельные нормалям к вертикальной и горизонтальной граням параллепипеда
до пересечения с окружностью в точке К (полюс круга). Направления ![]() и
и ![]() получатся,
если точки А и В соединить с полюсом К круга Мора,
имеющего координаты (
получатся,
если точки А и В соединить с полюсом К круга Мора,
имеющего координаты (![]() и
и ![]() ). Из построений можно получить выражения
для главных напряжений
). Из построений можно получить выражения
для главных напряжений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.