Современные предпосылки к моделированию механики нестационарных видов обработки резанием. Анализ экономической эффективности внедрения станка-автомата попутного точения мод. КА-350, страница 3

Еще И. А. Тиме в 1870 г. предложил, а К. А. Зворыкин в 1893 г. разработал модель зоны деформаций в виде единственной плоскости сдвига: плоскости, проходящей от вершины резца к некоторой точке, лежащей на свободной поверхности обрабатываемой заготовки. По обе стороны от этой плоскости пластические деформации отсутствуют. Однако экспериментальные наблюдения, показали, что пластическая деформация происходит в некоторой области (рисунок 1.5) – так называемая зона первичных деформаций [6, 8]. Эта зона имеет форму, близкую к клину, с вершиной на лезвии инструмента. Ее нижняя граница  вогнута и пересекает продолжение поверхности резания. Верхняя граница  зоны выпукла. Линия  плавно сопрягает предыдущую поверхность резания со свободной стороной стружки. Рассмотренная зона получила название зоны стружкообразования.

На сложность схематизации деформаций в зоне стружкообразования указывали А. А. Брикс, Н. Н, Зорев [[26]], Г. Л. Куфарев [[27]],  К. Окусима, К Хитоми, J. Pomey [[28]] и др. В тоже время Г. Л. Куфарев [27], И. Дж. А. Армарего [8] и др. отмечают, что вид этой зоны (применимость той или иной модели зоны деформаций) зависит от условий обработки. При резании с низкой скоростью, особенно при обработке металла в отожженном состоянии, более реалистичной является модель с развитой зоной деформаций и, наоборот, при обработке с высокими скоростями резания становится приемлемой модель деформаций с одной плоскостью сдвига, за счет их локализации в малых объемах.

Очевидно, что деформации приводят к возникновению напряженного состояния в УПС. В настоящее время нет единого мнения о законе распределения касательных и нормальных напряжений в условной плоскости сдвига. Наиболее широкое распространение получила гипотеза о равномерном распределении. За условие начала образования стружки принимают, что максимальные касательные напряжения в УПС достигают определенного предела t_р. Эту величину С. С. Силин и др.  называют сопротивлением пластическому сдвигу [[29]]. В соответствии с описанными теориями было предложено достаточно большое число методов для прогнозирования величины сопротивления сдвигу  по данным опытов на одноосное растяжение-сжатие.[6, 29, 26]. Все их можно обобщить следующей формулой:

,                                    ( 1.1)

где - константа данной группы материалов;  - предельные напряжения;                - коэффициент, учитывающий деформационное и скоростное упрочнение;  - коэффициент, учитывающий температурное разупрочнение. Значение указанных коэффициентов по данным различных авторов приведены в таблице :

Таблица 1.1 – Коэффициенты в формуле (1.1)

Автор					Примечание
С. С. Силин [29]			1	1	m – определяется экспериментально
Т. Н. Лоладзе [22]	1		1	1
В. С. Кушнер [[30]]	0,8		1	1	Ранние работы
В. С. Кушнер [[31]]	1		1		Для большинства сталей       , 1/С°
Н. Г. Абуладзе [22]	0,74			1
А.М. Розенберг [15]	2/3			1	,  - константы для данного металла и температурно-скоростного режима деформирования
Дж. Помей [28]	1			1	, ,  - константы материала

С другой стороны, касательные напряжения, возникающие в УПС могут быть определены через силы резания [6]:

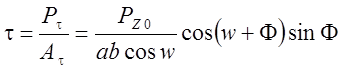  ,                              ( 1.2)

где  - угол действия,

либо по формуле [15]:

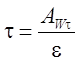 .                                                ( 1.3)

И. Дж. А. Армарего указывает [8], что вычисленные по первой из этих формул напряжения оказываются несколько завышенным по сравнению с величиной сопротивления сдвига. Отмечается, что объяснением этому могут служить внешние эффекты. Это, во-первых, эффект трения на задней поверхности. Сила трения на задней поверхности входит составной частью в изменяемую силу резания, но не влияет на процесс сдвига. Во-вторых, во многих случаях резания существует так называемая зона опережающего течения, которая увеличивает длину плоскости сдвига, хотя это и не учитывается при аналитическом исследовании.

В тоже время степень деформации может быть рассчитана по формуле[6; 15]:

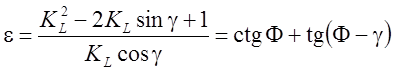.                                   ( 1.4)

Из этого уравнения следует, что при  степень деформации . Хотя хорошо видна однозначная функциональная зависимость .

Необходимо различать скорость сдвига  т. е. скорость, с которой осуществляется сдвиг по УПС, и скорость деформации , определяемы по формулам [6, 28]:

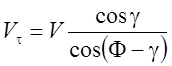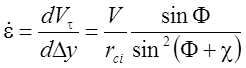;  ,                             ( 1.5)

где  - радиус кривизны линий течения [28]. Часто делается предположение, что скорость деформации является постоянной в УПС.

Большой интерес представляет прогнозирование угла сдвига. Для решения этой проблемы предложено огромное множество различных подходов. По мнению И. Дж. А. Армарего [стр. 50, 8] некоторые полученные формулы могут быть описаны общим выражением:

.                                               ( 1.6)

В таблице 1.2 приведена краткая характеристика постоянных  и . Необходимо отметить, что такой подход из всех условий обработки учитывает только передний угол и коэффициент трения. Угол сдвига  считается независимым от упрочнения, тепловых процессов, анизотропии и др. явлений, хотя в некоторых случаях эти формулы являются обобщением расчетов, учитывающие указанные особенности.

Помимо указанных соотношений известно много других (А.А. Виноградов[[32]], В.С. Кушнера  [30, 31], С.С. Силин [29], С.В. Мироненко [[33]]). Все они, как правило, носят более сложный характер и получены совместным решением известных уравнений, связывающих угол сдвига, усадку стружки, и температуру резания .

Таблица 1.2 - Коэффициенты формулы (1.6)