Министерство транспорта и связи Российской Федерации
Федеральное агентство по железнодорожному транспорту
ГОУ ВПО
Дальневосточный Государственный Университет
Путей Сообщения
Кафедра: "Электроснабжение транспорта"
КОМПЛЕКСНОЕ ЗАДАНИЕ
по дисциплине: «Применение ЭВМ в электроэнергетике»
КЗ
Выполнил:
Проверил:
Хабаровск
2009
Исходные данные.
1.1. Схема электрической сети.
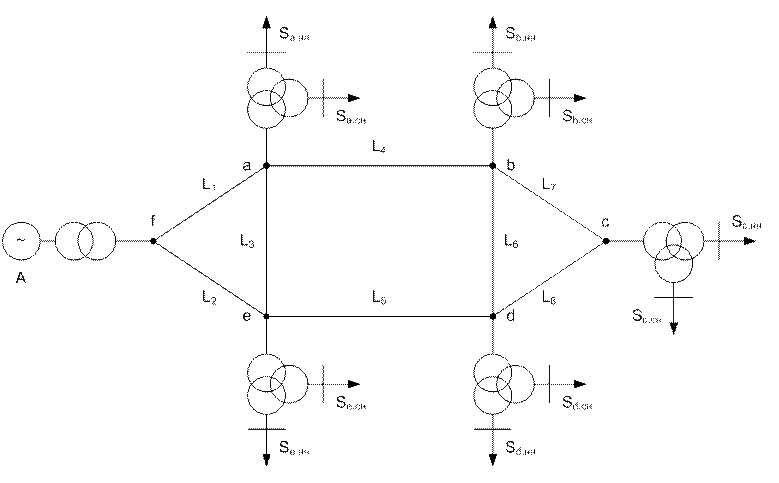
Рис. 1.1. Расчетная схема сети 110 кВ.
1.2. Нагрузка потребителей.
Таблица 1.1.
|
Узел сети |
Подстанция |
|||||||||
|
a |
b |
c |
d |
e |
||||||
|
Ном. мощность трансформатора, МВА |
40 |
16*2 |
25*2 |
63 |
40 |
|||||
|
Обмотка |
CH |
HH |
CH |
HH |
CH |
CH |
HH |
CH |
HH |
CH |
|
Полная мощность потребителей, МВА |
25 |
14 |
18 |
13 |
20 |
25 |
14 |
18 |
13 |
20 |
|
cosφ |
0.85 |
0.87 |
0.89 |
0.91 |
0.92 |
0.85 |
0.87 |
0.89 |
0.91 |
0.92 |
1.3. Длины участков сети.
Таблица 1.2.
|
№ линии |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Длина линии, км |
26 |
29 |
32 |
47 |
85 |
62 |
34 |
47 |
1.4. Номинальное напряжение сети – Uн=220 кВ.
1.5. Марка провода – АС-300.
Задача №1. Составление схемы замещения электрической системы и определение расчетных нагрузок подстанций.
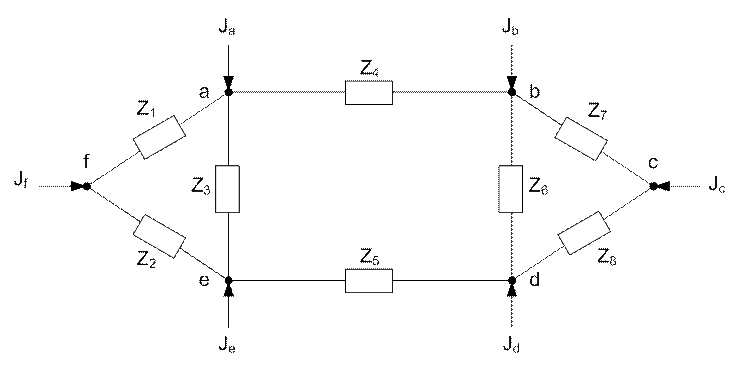
Рис. 2. Схема замещения.
Для заданной марки провода АС-150/24 из справочных материалов определяем удельные параметры:
![]() Ом/км;
Ом/км;
![]() Ом/км;
Ом/км;
![]() См/км.
См/км.
Полное сопротивление участков ЛЭП определяется по следующей формуле:
![]() , Ом.
, Ом.
Зарядная мощность участка ЛЭП:
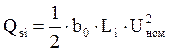 , Мвар.
, Мвар.
Пример для первого участка:
![]() Ом.
Ом.
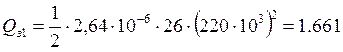 Мвар.
Мвар.
Результаты расчета сведем в табл. 1.
Таблица 1. Полные сопротивления участков ЛЭП.
|
Участок |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Zi, Ом |
2.808+j11.154 |
2,826+j11,716 |
3,119+12,928 |
4,581+j18,988 |
8,284+j34,34 |
6,043+j25,048 |
3,313+J13,736 |
4,581+j18,988 |
|
Qзi, Мвар |
1.661 |
1.85 |
2.04 |
3.0 |
5.43 |
3.901 |
2.172 |
3.0 |
Расчетные нагрузки в узлах схемы будем определять по следующей методике. Согласно заданной мощности трансформаторов выбираем из справочного материала тип трансформатора, сопротивления обмоток и потери мощности при холостом ходе.
Переменные потери в обмотках трансформатора определяются:
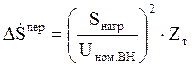 , МВА.
, МВА.
Расчетная нагрузка в узле определяется:
![]() , МВА.
, МВА.
Пример расчета для узла «а»:
Тип тр-ра: ТДТН – 40000/220
![]() МВА.
МВА.
![]() Ом.
Ом.
![]() Ом.
Ом.
![]() Ом.
Ом.
![]() Ом.
Ом.
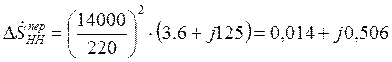 МВА.
МВА.
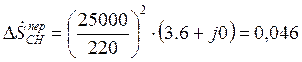 МВА.
МВА.
![]() МВА.
МВА.
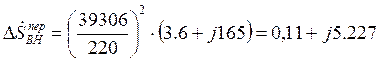 МВА.
МВА.
![]()
![]() МВА.
МВА.
Результаты расчета сведем в табл. 2.
Таблица 2. Расчетные нагрузки в узлах схемы замещения.
|
Узел |
а |
b |
c |
d |
e |
|
Sрасч, МВА |
33.655+22.353 |
28.34+j9,589 |
41.21+j24.36 |
49.59+j38.58 |
32.79+j19.73 |
Задача №2. Составление направленного графа схемы замещения, матриц инциденций M и N, матрицы сопротивлений в ветвях и диагональной матрицы сопротивлений.
Произвольно выбираем направления ветвей и обход контуров.
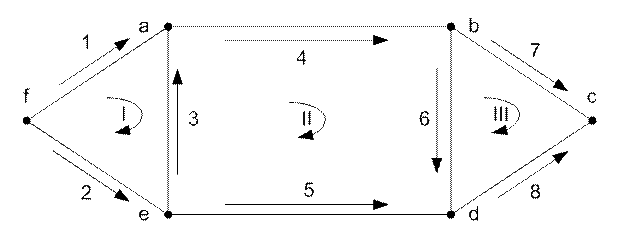
Рис.3. Направленный граф схемы замещения.
В качестве балансирующего узла выбираем узел «f».
Составим матрицу инциденций M. Количество строк равно количеству узлов без балансирующего =5, количество столбцов равно количеству ветвей =8. Ветви графа направленные к узлу обозначаются «-1», от узла – «1», не связанные с узлом – «0».
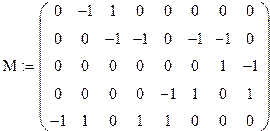
Составляем матрицу соединений ветвей в независимые контуры. Матрица N содержит число строк равное числу независимых контуров =3, число столбцов равное числу ветвей =8. Ветви графа, совпадающие по направлению с контуром, обозначаем «1», не совпадающие – «-1», не относящиеся к контуру – «0».
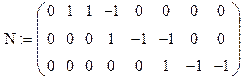
Проверка:
![]() .
.
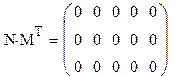
Составим столбцовую матрицу сопротивлений ветвей согласно табл. 1.
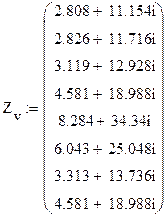
Диагональная матрица сопротивлений составляется на основании матрицы сопротивлений ветвей. Сопротивления ветвей располагаются на главной диагонали, остальные элементы равны нулю, так как отсутствуют взаимные индуктивности.
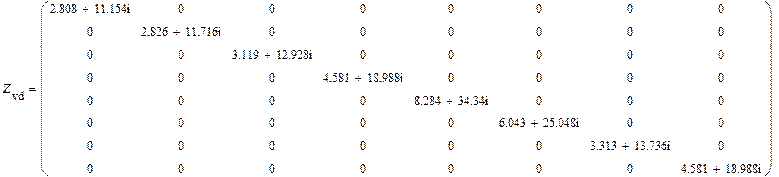
Задача №3. Определение матрицы проводимостей ветвей и матрицы узловых проводимостей, столбцовой матрицы задающих комплексных токов в узлах.
Для определения диагональной матрицы проводимостей ветвей необходимо взять обратную диагональную матрицу сопротивлений ветвей.
![]() .
.
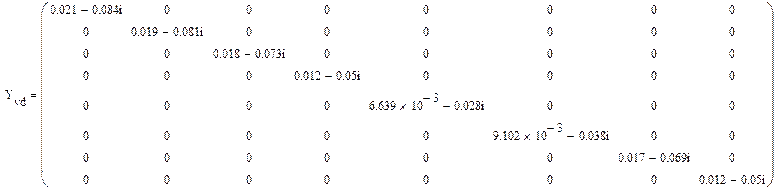
Определим матрицу узловых проводимостей по формуле:
![]() .
.
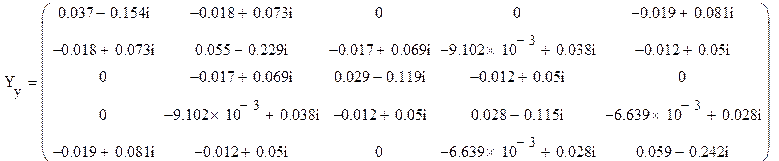
Столбцовая матрица задающих токов в узлах будет выглядеть:
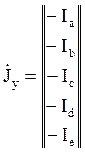 , А.
, А.
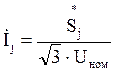 .
.
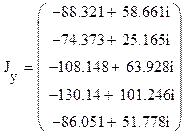 А.
А.
Задача 4. Определение напряжений в узлах прямым методом и методом итераций.
Прямой метод – метод, при котором задающие токи в узлах не зависят от напряжения.
Задача определения напряжений в узлах имеет единственное решение при заданных токах в узлах, если в одном из узлов напряжение задается (базисный узел).
Напряжение в базисном узле:
![]() кВ.
кВ.
Линейные падения напряжений от каждого из независимых узлов до базисного:
![]() кВ.
кВ.
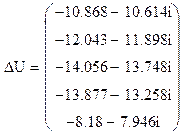 кВ.
кВ.
Напряжение в узлах по отношению к нейтрали:
![]() , где
, где
1 – единичная столбцовая матрица.
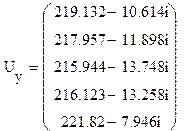 кВ.
кВ.
Определение напряжений методом итераций.
По значениям найденных напряжений пересчитываются задающие токи в узлах и определяются падения напряжений и значения напряжений в узлах. Для того чтобы итерационный процесс считался завершенным, должно выполниться условие:
![]() , где
, где
n – номер итерации;
![]() - допустимая
погрешность (0,01%).
- допустимая
погрешность (0,01%).
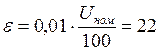 В.
В.
Рассчитаем задающие токи, зная напряжение в узлах:
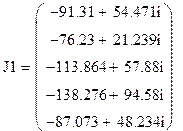 А.
А.
Падения напряжения:
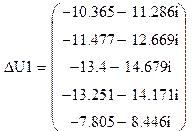 кВ.
кВ.
Напряжение в узлах:
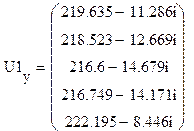 кВ.
кВ.
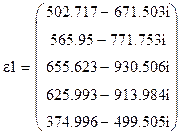 В.
В.
Так как условие не выполняется, итерационный процесс повторяется.
Результаты итераций:
2)
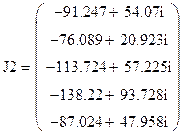 А,
А, 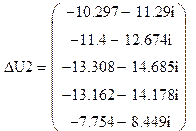 кВ,
кВ, 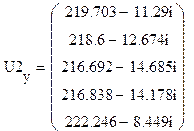 кВ,
кВ, 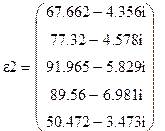 В.
В.
3)
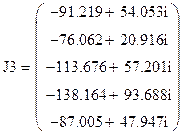 А,
А, 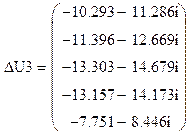 кВ,
кВ, 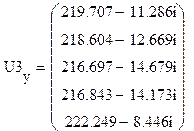 кВ,
кВ, 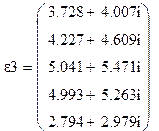 В.
В.
Таким образом, после 3-х итераций напряжения в узлах найдены с заданной точностью.
Задача 5. Составление объединенной матрицы параметров схемы замещения А и определение обратной матрицы А-1.
Для определения токов в ветвях используется обобщенное выражение в матричной форме:
![]() , где
, где
А – обобщенная матрица параметров схемы замещения.
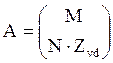 .
.
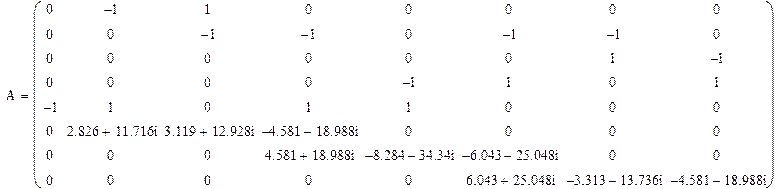
Обратная матрица А:
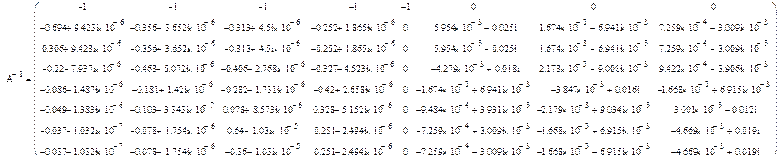
Задача №6. Определение токов в ветвях, потерь активной мощности в сети, составление баланса мощностей.
Матрица токов в ветвях определяется как:
![]() , где
, где
F – матрица:
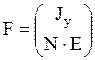 .
.
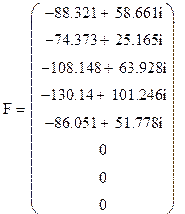 .
.
Матрица токов в ветвях:
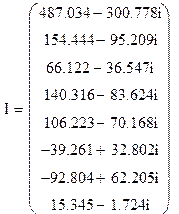 .
.
Определим потери полной мощности в сети, МВА:
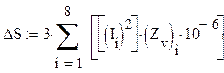
![]() .
.
Тогда потери активной мощности будут равны 7,834 МВт.
Ток источника питания по закону Кирхгофа будет равен сумме токов 1 и 2 участков, отсюда полная мощность источника питания будет определяться:
![]()
![]()
Мощность потребителей с учетом потерь мощности в трансформаторах и зарядных мощностей ЛЭП:
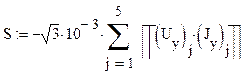
![]()
Суммарная мощность потребителей и потерь мощности во всех элементах сети:
![]()
![]()
Баланс полной мощности выполняется. Откуда можно сделать вывод, что расчет выполнен верно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.