

Задание:
Задача максимизация дохода от оптимальной выработки суточного количества электроэнергии, с использованием Симплекс метода:
Для обращения к функции linprogнеобходимо подготовить входную информацию:
|
Наименование |
Выработка электроэнергии, МВт·ч |
Ограничения |
|
|
Уголь |
Мазут |
||
|
Сырье, т/МВт·ч |
15 |
20 |
500 |
|
Котлоагрегаты, шт/ МВт·ч |
2 |
1 |
10 |
|
Турбоагрегаты |
2 |
1 |
7 |
|
Питательные электронасосы |
4 |
2 |
8 |
|
Доход (руб./ МВт·ч) |
1000 |
500 |
|
Математическая модель задачи линейного программирования с использованием «Симплекс» метода:
В начале составляются
линейные неравенства ![]()
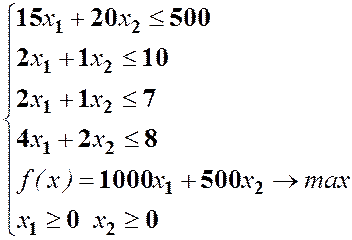
![]() вектор коэффициентов
целевой функции
вектор коэффициентов
целевой функции
> f = [1000; 500];
![]() матрицу коэффициентов
системы линейных неравенств
матрицу коэффициентов
системы линейных неравенств
> A = [15 20;2 1;2 1;4 2]
![]() вектор свободных членов
системы линейных неравенств
вектор свободных членов
системы линейных неравенств
> b = [500;10;7;8]
![]() вектор нижних границ для
переменных
вектор нижних границ для
переменных
> lb = zeros(2,1)
Определите значения суммарного дохода при выработке электроэнергии при работе на угле и мазуте fval, и кол-во электроэнергии при работе на разных энергонасителях xвоспользовавшись следующим выражением:
> [x,fval] = linprog(-f, A, b, [ ], [ ], lb)
Знак минус перед целевой функции нужен, чтобы обратить заложенный в программе процесс минимизации в определение максимума. Значение суммарного дохода определять по модулю.
Решите следующую задачу по оценке ресурсов. Задача заключается в определении доли каждого в отдельности наименования y (см. таблицу) на доход gval от выработанной электроэнергии. Т.е. при увеличении какого наименования можно увеличить доход.
Для решения этой задачи необходимо скорректировать вектор нижних границ:
> lb = zeros(4,1);
Обращение к функции linprog теперь имеет такой вид:
> [y,gval] = linprog(b, -A’, -f, [ ], [ ], lb)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.