Схема электроснабжения. Нагрузки потребителя. Параметры линий электропередачи. Суммарные потери активной мощности

Введение.

Дисциплина “Математические задачи электроэнергетики” связывает дисциплину “Высшая математика” с решением инженерных задач электроэнергетики.

В данной курсовой работе рассматривается методика расчета сложных электрических сетей при помощи матричной алгебры и теории графов.

1.  Схема электроснабжения и исходные данные.

1.1. Схема электроснабжения.

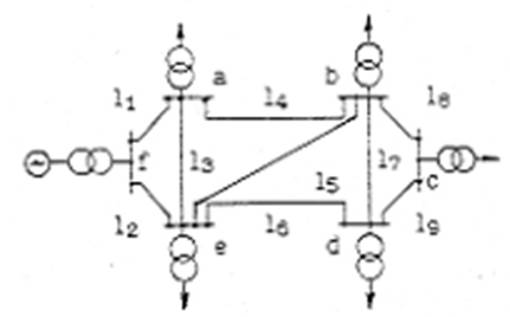Рис.1  Исходная схема электроснабжения.

1.2.  Нагрузки потребителя.

	Подстанции
	a	b	c	d	e
Мощность транс-ра, мВА	4	25	10	10	--
кол-во трансформаторов	2	1	1	1	--
Cos j	0,87	0,9	0,8	0,8	--

1.3. Параметры линий электропередачи.

Номинальное напряжение U_Н = 35кВ        Марка проводов АС

№ линии	l1	l2	l3	l4	l5	l6	l7	l8	l9
длина линии, км	18	14	15	27	48	32	20	9	14

2. Задание курсовой работы.

Для заданной схемы :

2.1. Составить схему замещения и её направленный граф для установившегося режима.

2.2. Составить матрицы инциденций M и N, проверить правильность составления по выражению NM_t=0, составить матрицы Z_B, Y_y, J, составить матрицу D₁, найти на ЭВМ матрицу D₁^-1.

2.3. Найти матрицы U_d, U_y, составить матрицу D₂, умножить её на матрицу U_d, определить токи ветвей.

2.4. Определить суммарные потери активной мощности.

3. Схема замещения и её направленный граф.

Для определения параметров установившегося режима (токов в линии, напряжений в узлах и ветвях и др.) исходную схему (рис.1) заменяю схемой замещения представленной на рисунке 2.

 

Рис.2    Схема замещения    

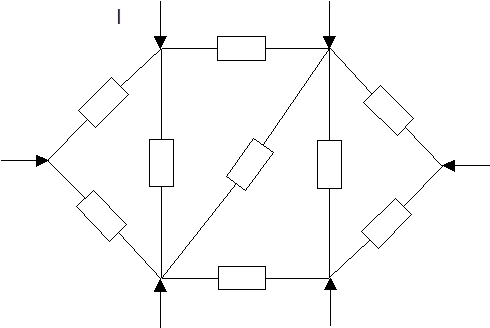Для определения токов в ветвях схемы, напряжений узлов и других параметров установившегося режима запишу на основании схемы замещения (рис.2) закон Кирхгофа в матричной форме, для чего заменю указанную схему соответствующим графом (рис.3).

Рис.3    Схема графа

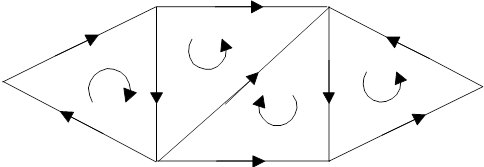На схеме графа выберу произвольно направление ветвей и направление обхода контуров. Выберу в качестве балансирующего узел f, после чего составлю матрицы инциденций M и N.

4.Составление матриц.

4.1. Матрицы инциденций.

Для графа на рис.3 матрица M будет иметь вид:

1   2   3   4   5   6   7    8    9                              

-1   0   1   1   0   0   0    0    0    a

0   0   0  -1  -1   0   1  -1    0    b

M =    0   0   0   0   0   0    0   1   -1    c

0   0   0   0   0   -1 –1   0    1    d

0   1  -1   0   1    1   0   0    0    e

А матрица N  будет следующего вида :

1     2     3     4      5     6     7     8      9

                                

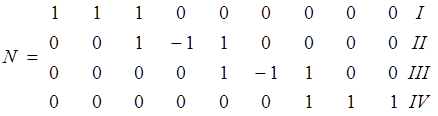
Правильность составления данных матриц проверяется следующим выражением:  NM_t=0, где M_t- транспонированная матрица M, то есть

M_t =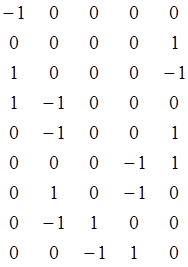  

Подставив значения в выражение NM_t и посчитав его при помощи математической программы “Maple V”, получю верное равенство,

то есть NM_t=0.

2.1. Составление матриц Z_B, Y_y, J, D_1.

Диагональная матрица сопротивления ветвей Z_B, для схемы рис.2, имеет вид :

 

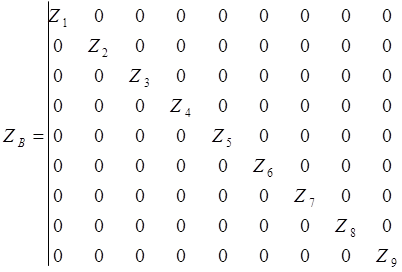Значение Z для каждой ветви находиться следующим образом :

Z = r₀l  +  jx₀l, где l – длина ветви, км; r₀ – погонное сопротивление, равное r₀ = r/S (r - удельное сопротивление, равное 32 Ом мм²/км;

S – сечение провода, равное 70 мм²); x₀ – можно принять 0,38 Ом/км; подставив значения получю следующие сопротивления:

Z₁=8,226 +  j6,84 Ом ;   Z₂= 6,398 + j5,32  Ом ;   Z₃=6,855 +  j5,7 Ом ; 

Z₄=12,339 + j10,26 Ом ;   Z₅=21,936 + j18,24 Ом ;   Z₆=14,624 + j12,16 Ом; Z₇=9,14 + j7,6 Ом ;   Z₈=4,113 + j3,42 Ом ;   Z₉=6,398 + j5,32 Ом

8,226+j6,84          0                   0                  0                      0                     0                   0                0                      0      

0          6,398+j5,32           0                  0                      0                     0                   0                0                      0

0                   0           6,855+j5,7           0                      0                     0                   0                0                      0    

0                   0                    0       12,339+j10,26           0                     0                   0                0                      0  

0                   0                    0                   0          21,936+j18,24          0                   0                0                      0

0                   0                    0                   0                      0          14,624+j12,16        0               0                      0

0                   0                    0                   0                      0                     0          9,14 + j7,6        0                      0

0                   0                    0                   0                      0                     0                  0         4,113 + j3,42          0

0                   0                    0                   0                      0                     0                  0                0            6,398 + j5,32

0