Основные методы интегрирования.
I. Интегрирование заменой переменного.
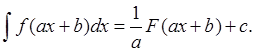
II. Интегрирование по частям.
Формула интегрирования по частям: ![]()
Интегралы, «берущиеся» по частям:
1)
![]() где
где ![]() не- который многочлен степени
не- который многочлен степени ![]() .
.
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)

17)
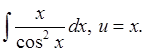
III. Интегрирование дробно-рациональных функций.
Алгоритм решения:
1) Выясняем, правильная дробь или неправильная. Если дробь неправильная, то выделяем целую часть с помощью деления числителя на знаменатель.
2) Если знаменатель правильной дроби раскладывается на множители, то раскладываем эту дробь на элементарные дроби с помощью метода неопределенных коэффициентов или метода частных значений.
Интегралы от простейших дробно-рациональных функций:
1)
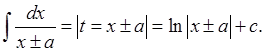
2)
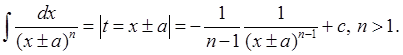
3)
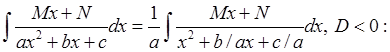
a) выделяем полный квадрат знаменателя:
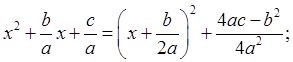
b)
делаем замену переменного: 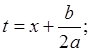
c)
получим интеграл вида: 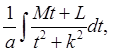 где
где 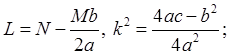
d)
первое слагаемое 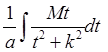 интегрируется заменой
интегрируется заменой ![]() а второе слагаемое
а второе слагаемое 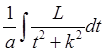 является
табличным интегралом.
является
табличным интегралом.
4)
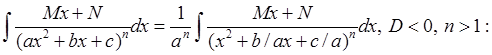
a)
как и в случае 3) выделяем полный
квадрат знаменателя и делаем замену переменного: 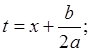
b)
получим интеграл вида: 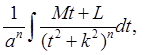 где
где 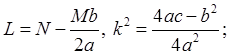
c)
первое слагаемое  интегрируется заменой
интегрируется заменой ![]() а второе слагаемое
а второе слагаемое 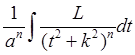 вычисляется
тригонометрической подстановкой
вычисляется
тригонометрической подстановкой ![]() или по формуле
приведения
или по формуле
приведения
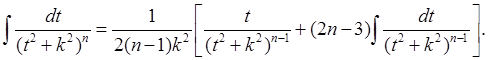
IV. Интегрирование тригонометрических функций.
1)
Для интегралов![]()
![]()
![]() пользуемся формулами:
пользуемся формулами:
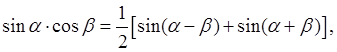
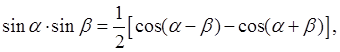
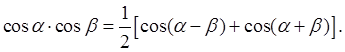
2)
![]()
a)
![]() -четные,
-четные,
![]() понижаем степень по формулам:
понижаем степень по формулам: 
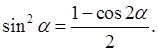
b)
![]() -
четное,
-
четное, ![]() - нечетное,
- нечетное, ![]()
c)
![]() -
нечетное,
-
нечетное, ![]() - четное,
- четное, ![]()
d)
![]() -
нечетные, поступаем либо как в случае а), либо как в случае b).
-
нечетные, поступаем либо как в случае а), либо как в случае b).
3)
![]() пользуемся
основной тригонометрической подстановкой:
пользуемся
основной тригонометрической подстановкой: 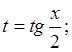 тогда
тогда 
4)
![]() или
или 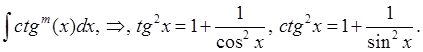
Пример. 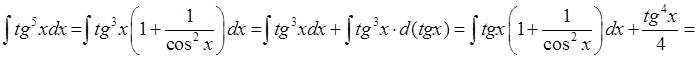

V. Интегрирование иррациональностей.
1)
![]()
2)
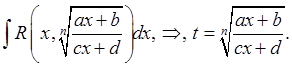
3)
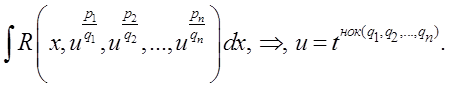
4)
![]() «по
частям»
«по
частям» ![]() или заменой
или заменой ![]()
5)
![]() «по
частям»
«по
частям» ![]() или заменой
или заменой 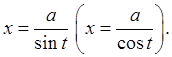
6)
![]() «по
частям»
«по
частям» ![]() или заменой
или заменой ![]()
7)
![]() выделяем
полный квадрат в подкоренном выражении и в зависимости от знака
выделяем
полный квадрат в подкоренном выражении и в зависимости от знака ![]() получим интеграл либо из пункта 4), либо
5), либо 6).
получим интеграл либо из пункта 4), либо
5), либо 6).
8)
![]()
9)
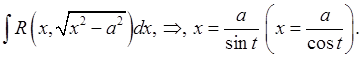
10)
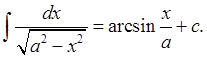
11)
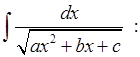
a)
выносим из под корня ![]() (чтобы коэффициент при
(чтобы коэффициент при ![]() был равен 1 или -1);
был равен 1 или -1);
b) выделяем полный квадрат в подкоренном выражении;
c)
делаем замену переменного и в
зависимости от знака ![]() получим интеграл либо из пункта
8), либо 9), либо 10).
получим интеграл либо из пункта
8), либо 9), либо 10).
12)
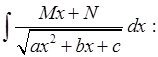
a)
выносим из под корня ![]() ;
;
b) выделяем полный квадрат в подкоренном выражении;
c) делаем замену переменного;
d)
разбиваем на два интеграла, один
из которых «берется» заменой переменного, а второй в зависимости от знака ![]() является интегралом либо из пункта 8),
либо 9), либо 10).
является интегралом либо из пункта 8),
либо 9), либо 10).
13)
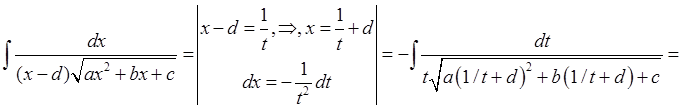
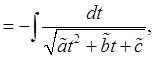 где
где ![]() Таким образом, данный интеграл «свели» к интегралу из
пункта 11.
Таким образом, данный интеграл «свели» к интегралу из
пункта 11.
14) Все остальные интегралы, содержащие квадратичную иррациональность, можно свести к дробно-рациональной функции с помощью подстановок Эйлера:
a)
![]()
b)
![]()
c)
![]() или
или ![]() , где
, где ![]() - корни
уравнения
- корни
уравнения ![]()
15) Для «взятия» интегралов, содержащих квадратичную иррациональность, удобно тождество:
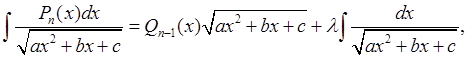 (1)
(1)
где ![]() многочлены степени
многочлены степени ![]() и
и ![]() соответственно,
причем многочлен
соответственно,
причем многочлен ![]() записан в общем виде. Задача
состоит в отыскании коэффициентов многочлена
записан в общем виде. Задача
состоит в отыскании коэффициентов многочлена ![]() и числа
и числа
![]() . Для этого «берем» производную от левой и
правой части равенства (1):
. Для этого «берем» производную от левой и
правой части равенства (1):
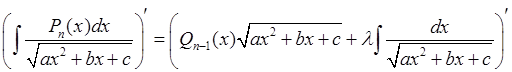
и применяем метод неопределенных коэффициентов.
16)
Интеграл от биномиального
дифференциала ![]() :
:
a)
если ![]() целое
число, тогда интеграл подходит под тип из пункта 3;
целое
число, тогда интеграл подходит под тип из пункта 3;
b)
если ![]() дробь
дробь 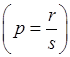 , но
, но 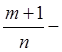 целое
число, тогда используем подстановку
целое
число, тогда используем подстановку ![]()
c)
если оба числа  и
и 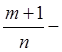 дробные,
но их сумма
дробные,
но их сумма 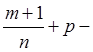 целое число, тогда используем подстановку
целое число, тогда используем подстановку ![]()
Замечание. Вычислить интегралы из пунктов 8 и 9 можно с помощью подстановок Эйлера следующим образом:
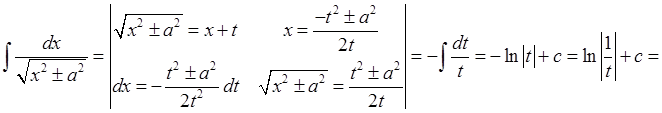
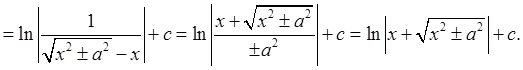
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.