Информатика и выч. техника \ Информатика

Примеры задач для итоговой контрольной работы и экзамена. Таблица значений функции. Построение таблиц значений функций

Страницы работы

2 страницы (Word-файл)

Скачать файл

Содержание работы

ПРИМЕРЫ ЗАДАЧ ДЛЯ ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЫ И ЭКЗАМЕНА

1. Задана таблица значений некоторой функции:

x	-1	0	1	2
F	0.5	0.2	-0.1	-0.2

Выписать базисные полиномы для построения полинома Лагранжа. Вычислить значение полинома Лагранжа (Ньютона) в точке z=0.5

2. Задана таблица значений функции

x	0	0.1	0.3	0.5	0.7	0.9	1.1	1.3	1.5
F	0	0.1	0.296	0.479	0.717	0.783	0.841	0.99	1

Вычислить значение с помощью метода трапеций (левых прямоугольников, правых прямоугольников, Симпсона).

3. Вычислить значение с помощью метода трапеций (левых прямоугольников, правых прямоугольников, Симпсона) на сетках с шагами h=0.4 и h=0.2 .

4. СЛАУ записана в виде x=ax+b , где

	0.23	-0.04	0.21	-0.18		0.23		x₁
a=	0.45	-0.23	0.06	0	b=	0.45	x=	x₂
	0.26	0.34	-0.11	0		0.26		x₃
	0.05	-0.26	0.34	-0.12		0.05		x₄

Решить систему с помощью метода простой итерации с точностью e=0.05. Начальное приближение x⁰=(0,0,0,0).

5. Задана СЛАУ

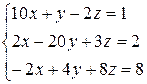
Проверить выполнение условия диагонального пребладания и решить СЛАУ помощью метода Якоби (точность 0.05). Начальное приближение x₀=(0,0,0,0).

6. Задана таблица значений некоторой функции:

X	-2	0	1	4
F	0.5	-1	-1.2	0

C помощью метода наименьших квадратов найти коэффициенты a, b, c функции P(x)=a+bx+cx², наиболее приближенной к заданным точкам СЛАУ решить с помощью метода Крамера (Гаусса). Для найденной функциональной зависимости P(x) вычислить сумму квадратов отклонений по всем точкам.

7. Построить таблицу значений функции y=cos(x) на отрезке [0, p] с шагом p/4. Найти производную по формулам разностного дифференцирования во всех точках сетки со вторым порядком аппроксимации. Сравнить с точным значением производной.

8. С помощью явного метода Эйлера (Рунге-Кутты, предиктор-корректор) построить таблицы приближенного решения задачи Коши для ОДУ 1 порядка: на сетках с шагами t=0.2 и t=0.1.

9. С помощью явного метода Эйлера (Рунге-Кутты) построить таблицы приближенного решения задачи Коши для системы двух ОДУ 1 порядка: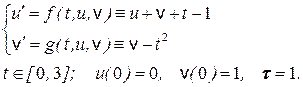

10. Написать разностную схему для решения краевой задачу для ОДУ второго порядка на сетке с шагом t=0.1. Выписать СЛАУ на вектор приближенного решения и решить ее методом прогонки.