

Лабораторная работа 3.
Подбор полиномиальной зависимости методом наименьших квадратов. Решение СЛАУ.
1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)
Задана система точек (узлы интерполяции) xi , i = 1,2,...,N; a £ xi £ b, и значения fi, i = 1,2,....,N. Требуется построить многочлен 3-ей степени P3(x)=a1+a2x+a3x2+a4x3, имеющий в узлах интерполяции минимальное отклонение от заданных значений fi. В i-ой точке полином P3(x) отклоняется от значения fiна величину (P3(xi)-fi). Суммируя квадраты отклонений полинома по всем точкам i=1,2,…N, построим функционал
![]() .
.
Найдем min![]() .
Для этого приравняем нулю все частные производные
.
Для этого приравняем нулю все частные производные ![]() . Собирая
коэффициенты при неизвестных ai, получим нормальную
систему ‑ СЛАУ относительно вектора
. Собирая
коэффициенты при неизвестных ai, получим нормальную
систему ‑ СЛАУ относительно вектора ![]()
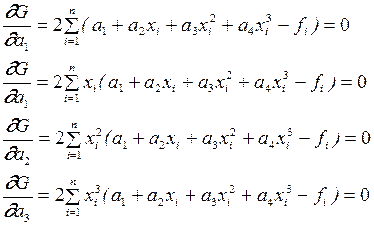
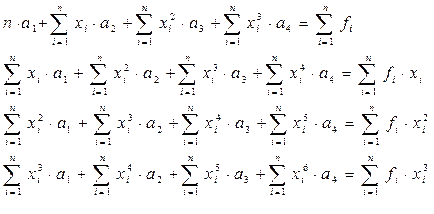
![]()
В матричном виде систему можно записать: Ba = C. (1)
B – матрица системы, a – искомый вектор, с – вектор правой части. Решение СЛАУ найдем с помощью точного метода Гаусса, а также с помощью итерационного метода релаксации.
2. МЕТОД РЕЛАКСАЦИИ
ШАГ 1. Запишем систему (1) в виде a = a ‑ t ( B a – c), t > 0 ‑ параметр, значение которого подбирается таким образом, чтобы построенный итерационный метод сходился.
ШАГ 2. Зададим точность метода e>0, параметр релаксации t > 0, введем вектор начального приближения к решению a0. Вектор может быть произвольным, например, нулевым:.a0 = (0, 0, ..., 0).
ШАГ 3. Следующее приближение ‑ вектор a1находится следующим образом: a1 = a0 ‑ t ( B a0 – c), или, в скалярном
виде: 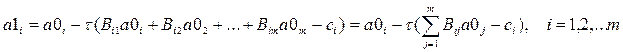
ШАГ 4. Вычислим вектор невязки: r = a1 – a0 и его норму: ║ r ║ = max ( r i )..
ШАГ 5. Приготовимся к следующей итерации. Занесем компоненты вектора a1в вектор a0, т.е. a0i:=a1i. I=1,2..m.
ШАГИ 3-5 образуют итерационный цикл. Будем повторять их до тех пор, пока не выполнится условие ║ r║ < e.
3. ВЫПОЛНЕНИЕ ЗАДАНИЯ
1. Открыть файл MNK.xls в папке своей группы, найти рабочий лист с номером своего варианта. Используя функцию суммирования Excel, вычислить коэффициенты матрицы B и вектора правых частей c.
2. Используя встроенные функции Excel (см рабочие листы Пример 3, Пример 4, Пример 5 в файле MNK.xls), решить СЛАУ методом обратной матрицы и методом Крамера. Выписать искомый полином, построить его график и нанести заданные точки.
3. Запустить тестовый вариант программы метода Гаусса (программа gauss_t.pas). Должны получиться следующие результаты: 2.2133, 0.0781, -3.6163, 2.4822.
4. Изменить исходные данные программы метода Гаусса (матрицу B и вектор с) и найти решение (коэффициенты полинома) для своего варианта. На печать вывести коэффициенты полинома и значение функционала отклонений G для найденных значений коэффициентов. Показать, что для любого другого вектора, произвольно введенного с клавиатуры, получится большее значение функционала отклонений G.
5. Написать программу решения системы (1) с помощью метода релаксации для e=10-3. Для подбора значения параметра t, обеспечивающего сходимость итерационного процесса, на каждой итерации выводить на экран промежуточные результаты – вектор a1и норму вектора невязки ║ r ║. В случае, если невязка растет, остановить выполнение программы (<ctrl>+<C>), заново запустить ее и задать меньшее значение t. Результаты занести в Таблицу 1:
|
t |
Сходимость процесса |
|
1 |
Не сходится |
|
0.5 |
Не сходится |
|
0.25 |
Не сходится |
|
0.1 |
Сходится |
6. После выбора значения t, обеспечивающего сходимость итерационного процесса, убрать промежуточную печать и добавить в программу счетчик количества итераций. Для e=10-3 подобрать оптимальное значение параметра, т.е. такое значение, при котором метод сходится с наименьшим количеством итераций. Результаты занести в Таблицу 2:
|
t |
Количество итераций для e=10-3 |
|
0.1 |
240 |
|
0.15 |
300 |
|
0.125 |
150 |
7. Для оптимальногозначения параметра t просчитать варианты с изменением точности e=10-2, 10-3, 10-4. Сравнить полученные результаты a1, a2, a3, a4 с результатами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.