Численные методы и их реализация на ЭВМ. Аппроксимация функций. Конечные разности. Интерполяционные формулы Ньютона

рассмотрим два способа аппроксимации: интерполирование и выбор эмпирической зависимости.

Интерполирование функций

Постановка задачи

Пусть на отрезке  в n+1 точке заданы значения функции y=f(x):

x	x0     x1     x2 … xn
y	y0       y1       y2   …     yn

где x_i , i=0,…, n – узлы интерполяции.

Требуется построить функцию(аппроксимирующую) такую, что в узлах интерполяции функция  будет совпадать со значениями f(x), т.е.

.

Используя построенную функцию , можно, например, найти приближенные значения функции f(x)  в точках, отличных от узлов интерполяции. В сформулированной постановке задача имеет бесчисленное множество решений. Однозначной задача становится в том случае, если вместо произвольной функции  искать полином (многочлен)

степени не выше n, удовлетворяющий условиям:

.

Рассмотрим один из возможных способов построения интерполяционного полинома .

Конечные разности

Если значения функции в таблице заданы для равностоящих значений аргумента

                    - шаг, то можно определить конечные разности функции  

Назовем конечной разностью первого порядка разность между значениями функции в соседних узлах интерполяции.

,

,

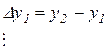Для i – го узла имеем

.

Аналогично можно ввести конечную разность второго порядка:

 

Конечные разности любого порядка выражаются соотношением:

.

При вычислении конечных разностей удобно пользоваться таблицей:

x	y

Интерполяционные формулы Ньютона

Пусть задана таблица n+1 значений функции y=f(x) для равностоящих узлов:

x	x0     x1   … xn
y	y0       y1   …     yn

x_{i =}x₀ +ih,  i=0,1,2,…,n.

Требуется построить полином  степени не выше n, удовлетворяющий условию . Будем искать  в виде

.

Используя условия  можно найти все коэффициенты . Эти коэффициенты выражаются через конечные разности. Полагая , находим . Далее, придавая xзначения x₁ и x₂, получаем

, откуда ;

, т.е.

, или  , откуда

.

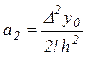Проведя аналогичные выкладки, можно получить:

.

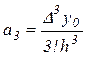В общем случае выражение , будет иметь вид:

.

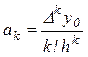Подставим найденные коэффициенты в выражение для многочлена, получим первую интерполяционную формулу Ньютона в виде:

.

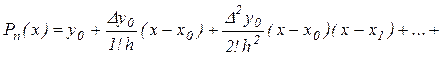
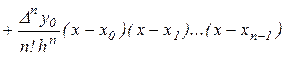Для практического использования эту формулу записывают по другому. Введем . Тогда

.

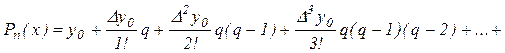
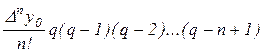Первую интерполяционную формулу Ньютона обычно используют, если необходимо найти значение интерполируемой функции для значения аргумента, лежащего ближе к началу таблицы. При этом следует помнить, что в качестве  мы должны брать ближайший меньший к заданному значению xузел таблицы, а совсем не обязательно первый узел. Если нам необходимо вычислить значение искомой (интерполируемой) функций для значений, лежащих ближе к концу таблицы, то следует использовать вторую интерполяционную формулу Ньютона, кот_орая имеет вид:

.

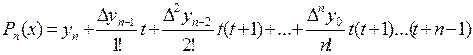Здесь .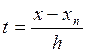

Эмпирические формулы

Задача выбора эмпирической формулы относится к разделу аппроксимации функций и отличается от задачи интерполирования тем, что 1) заранее не задается вид аппроксимирующей функции как полином n-й степени; 2) не требуется совпадения значений аппроксимирующей функции в узлах с табличными значениями.

В качестве эмпирической формулы обычно выбирается аналитическое выражение, которое достаточно хорошо согласуется с табличными данными.

Постановка задачи.

Пусть функция y(x) представлена в табличном виде:

x1	x2	x3	…	xi	…	xm
y1	y2	y3	…	yi	…	ym

Требуется найти эмпирическую формулу

                                  (3.1)

“наиболее хорошо” описывающую табличные данные.

Здесь  - параметры, число которых n+1<m.

Эта задача разбивается на этапы:

1)  выяснение общего вида формулы (линейная, параболическая, гиперболическая и т.д.);

2)  определение “наилучших” параметров выбранной эмпирической формулы.

Рассмотрим каждый этап подробно.

Выбор вида эмпирической формулы

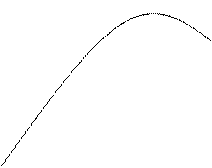
Практически вид эмпирической формулы можно определить следующим образом. По таблице исходных данных строится точечный график функции y(x), а затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек :

        y

 

y_n   

         

       y₂                                                        

       

       y₁ 

 

x₁     x₂      x₃                   x_n               x  

По полученной таким образом кривой устанавливается общий вид эмпирической зависимости.

Метод наименьших квадратов для отыскания параметров

эмпирической формулы

Условия, заложенные в основу выбора “наилучших” параметров различны. Достаточно простым и эффективным способом подбора “наилучших” параметров является метод наименьших квадратов (МНК),  который заключается в следующем. При подстановке различных значений x_i в формулу (3.1) получим в правой части . Эти значения за счет ошибок эксперимента, ошибок вычислений и т.п. не будут равны табличным значениям , т.е. мы имеем отклонение исходных значений  от вычисленных по формуле (3.1)

.

По МНК  подбираются так, чтобы сумма квадратов отклонений была