Математика \ Высшая математика

Методы решения систем линейных уравнений. Метод обратной матрицы. Метод простой итерации. Метод Гаусса – Зейделя

Страницы работы

2 страницы (Word-файл)

Скачать файл

Содержание работы

Лабораторная работа №2

«Методы решения систем линейных уравнений»

1. Постановка задачи

Найти для своего варианта решение системы линейных уравнений

1) Методом обратной матрицы .

2) Методом простой итерации с точностью ;

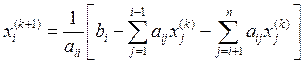
3) Методом Гаусса – Зейделя с точностью ;

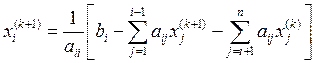
Здесь К-номер итерации, N-количество уравнений, -начальное приближение.

2. Решение

1) Метод обратной матрицы

7	2	2	2	*	0,1	=	0,0062679
4	13	4	4		0,2		0,0069644
6	6	15	2		0,3		0,0137239
8	8	8	25		0,4		0,007374

2) Метод простой итерации

k	x1	x2	x3	x4	d
0	0	0	0	0
1	0,014286	0,015385	0,02	0,016	0,02
2	-0,0004	-8,8E-05	0,005999	0,000105	0,015894505
3	0,012567	0,013628	0,020179	0,014235	0,014180806
4	0,000559	0,000929	0,007624	0,00116	0,013074983
5	0,011511	0,01251	0,01925	0,013084	0,011923945
6	0,001473	0,001894	0,008647	0,002153	0,010930679
7	0,010659	0,011608	0,018366	0,012155	0,01000192
8	0,002249	0,002714	0,009473	0,002998	0,009157866
9	0,009947	0,010856	0,017615	0,011381	0,008383219
10	0,002899	0,003402	0,010161	0,003706	0,007674665
11	0,009352	0,010226	0,016985	0,010732	0,007025824
12	0,003445	0,003979	0,010738	0,0043	0,006431891
13	0,008852	0,009697	0,016457	0,010188	0,005888151
14	0,003902	0,004462	0,011222	0,004798	0,005390382
15	0,008434	0,009255	0,016015	0,009732	0,004934692
16	0,004285	0,004867	0,011627	0,005215	0,004517525

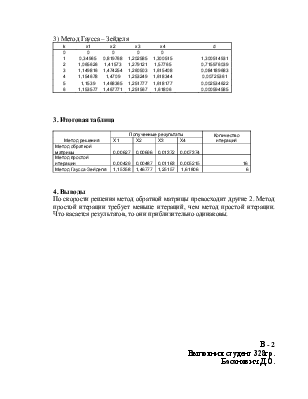
3) Метод Гаусса – Зейделя

k	x1	x2	x3	x4	d
0	0	0	0	0
1	0,34965	0,819768	1,202585	1,300515	1,300514931
2	1,065626	1,41573	1,279121	1,57765	0,715976039
3	1,149816	1,474254	1,260503	1,615408	0,084189683
4	1,154678	1,4709	1,253249	1,618344	0,00725361
5	1,1539	1,468365	1,251777	1,618177	0,002534622
6	1,153577	1,467771	1,251567	1,61806	0,000594585

3. Итоговая таблица

Метод решения	Полученные результаты				Количество итераций
Метод решения	X1	X2	X3	X4	Количество итераций
Метод обратной матрицы	0,00627	0,00696	0,01372	0,007374
Метод простой итерации	0,00429	0,00487	0,01163	0,005215	16
Метод Гаусса-Зейделя	1,15358	1,46777	1,25157	1,61806	6

4. Выводы

По скорости решения метод обратной матрицы превосходит другие 2. Метод простой итерации требует меньше итераций, чем метод простой итерации. Что касается результатов, то они приблизительно одинаковы.

В - 2

Выполнил студент 328гр.

Басанович Д.О.