Математика \ Высшая математика

Методы решения систем линейных уравнений. Оформление вычислений для различных методов. Точность метода итерации

Страницы работы

2 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Лабораторная работа №2

Методы решения систем линейных уравнений

ЗАДАНИЕ. Найти для своего варианта решение системы линейных уравнений :

1. Методом обратной матрицы , используя функции Excel МУМНОЖ и МОБР.

2. Методом простой итерации с точностью e=0,001;

3. Методом Гаусса – Зейделя с точностью e=0,001.

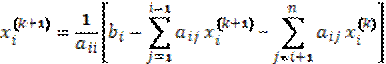
Здесь k – номер итерации, n – количество уравнений, – начальное приближение.

Оформить вычисления для методов 2, 3 в виде таблиц:

k	X₁	X₂	X₃	…	X_n	D
0				…		-
1				…		D¹
…	…	…	…	…	…	…

Где . Вычисления заканчиваются, когда D<e.

Решение

1. Метод обратной матрицы.

21	-2	-4	-6	-8	*	0,05	=	0,092685
1	17	-3	-5	-7		0,2		0,090481
2	0	13	-4	-6		0,45		0,094063
3	1	-1	11	-5		0,8		0,092373
4	2	0	-2	9		1,25		0,098116

2. Метод простой итерации.

k	x1	x2	x3	x4	x5	d
0	0	0	0	0	0
1	0,002381	0,011765	0,034615	0,072727	0,138889	0,138888889
2	0,083784	0,096313	0,120729	0,137287	0,151378	0,086113886
3	0,131442	0,130852	0,133834	0,120905	0,110757	0,04765812
4	0,117073	0,108817	0,102713	0,087494	0,07826	0,033410372
5	0,087121	0,080962	0,079645	0,075816	0,082118	0,029952014
6	0,078207	0,076807	0,082441	0,086174	0,099025	0,016906673
7	0,087744	0,087833	0,094802	0,096922	0,106212	0,012361389
8	0,096957	0,095574	0,099959	0,097709	0,101911	0,009213098
9	0,097263	0,094402	0,096799	0,093006	0,096271	0,005639949
10	0,093058	0,090121	0,092702	0,090179	0,095351	0,004281008
11	0,090711	0,088435	0,092054	0,090924	0,097543	0,002346815
12	0,091475	0,08958	0,093656	0,092655	0,099126	0,001730818
13	0,092987	0,090979	0,094802	0,093207	0,098917	0,001511958
14	0,093416	0,091169	0,094643	0,092677	0,098057	0,000859967
15	0,092925	0,090605	0,094016	0,092137	0,097706	0,000626255
16	0,092464	0,090221	0,093764	0,092106	0,097929	0,000460893
17	0,092456	0,090286	0,093929	0,092345	0,098213	0,000283436
18	0,09267	0,090503	0,094134	0,092485	0,098255	0,000216659
19	0,092786	0,090585	0,094164	0,092445	0,098143	0,000116028
20	0,092745	0,090526	0,094082	0,092358	0,098064	8,73812E-05
21	0,092669	0,090455	0,094025	0,092331	0,098076	7,62497E-05
22	0,092648	0,090447	0,094034	0,092359	0,09812	4,35419E-05
23	0,092673	0,090476	0,094066	0,092386	0,098137	3,17038E-05
24	0,092696	0,090495	0,094078	0,092387	0,098125	2,30443E-05
25	0,092696	0,090491	0,09407	0,092375	0,098111	1,4232E-05
26	0,092686	0,09048	0,094059	0,092368	0,098109	1,09602E-05
27	0,09268	0,090476	0,094058	0,09237	0,098115	5,73183E-06
28	0,092682	0,090479	0,094062	0,092374	0,098119	4,40988E-06
29	0,092686	0,090483	0,094065	0,092376	0,098118	3,84373E-06

3. Метод Гаусса – Зейделя

k	x1	x2	x3	x4	x5	d
0	0	0	0	0	0
1	0,002381	0,011625	0,034249	0,074135	0,151722	0,151721808
2	0,088992	0,096852	0,11376	0,118958	0,10425	0,086610868
3	0,106976	0,103461	0,102875	0,090885	0,088549	0,028073462
4	0,09153	0,087727	0,089367	0,088163	0,098306	0,015734024
5	0,090398	0,088627	0,093207	0,093174	0,099723	0,005010844
6	0,093186	0,091198	0,094974	0,092985	0,09787	0,002788481
7	0,093008	0,090702	0,094088	0,092156	0,097875	0,000885963

Вывод:

1. По скорости решения метод обратной матрицы превосходит другие 2. Метод Гаусса – Зейделя требует меньше итераций, чем метод простой итерации. Что касается результатов, то они приблизительно одинаковы.

В – 19

Выполнил студент 328гр. Протасов И.